Asymptotique en l'infini
Le développement asymptotique de lnΓ peut être obtenu par la formule d'Euler-Maclaurin. Fonctions dominées et négligeables 4. ] Rappel : Continuité d’une fonction Soient un intervalle, une fonction définie (au moins) sur et un réel tel que .Nous en déduirons l'existence éventuelle d'une asymptote et la position relative de la courbe et de son asymptote (localement). Chapitre 4 Étude d'une fonction : Limites et asymptotes. Nous allons proposer d’examiner les situations où « la courbe Cf C f se rapproche d’une droite » appelée asymptote dans les cas . Asymptotes horizontales. Nous allons calculer les 2 limites suivantes pour trouver des asymptotes : Puis nous montrerons que la droite d’équation. Limite fini à l’infini (Asymptote horizontale) : Lorsque x s'en va vers + f, f(x) se rapproche de plus en plus du réel b.1 Développements asymptotiques Un premier exemple On considère la fonction définie par f x x x x x af 2 2 1 3. Pour les articles homonymes, voir Stirling .Trigonométrie.
Asymptotes et branches infinies
On considère la fonction définie par .
Etude des branches infinies
C f a pour direction asymptotique la droite d'équation y = ax. Dans ce chapitre, on supposera choisie une échelle de comparaison E . Combinaison et composition de fonctions.
limite d'une fonction en l'infini. Développements asymptotiques et développements généralisés . Dérivée d'une fonction. Limites infinies et asymptotes.La structure asymptotique de la théorie d'Einstein est particulièrement riche et fait apparaître à l'infini des algèbres de symétrie infini-dimensionnelles. Limite d'une fonction - asymptote. Attention : ce n’est pas certain. limite d'une fonction en l'infini. Un développement asymptotique d'une . 1 - Asymptote . Les dérivées au service du graphique d'une fonction.Calcul d’asymptotes.—Si l’une tend vers l’infini ou vers 0 ena, alors l’autre en fera de même et le fera «à la même vitesse»; —Si l’une n’admet pas de limite en a, alors l’autre non plus mais elle «divergera de la même façon». La méthode de la phase stationnaire .nettechno-science. Suites équivalentes 3. Deux suites (un) et (vn) sont dites équivalentes si, et seulement si, lim . Puis j'ai exprimé le développement limité de x ln (1+1/x) en l'infini, mais il me reste un ln x .Ondit que ∆ est une direction asymptotique de C f en x 0 si lim x→x0,x∈I . un On dit que la suite (un)n est n ́egligeable par . Limite à gauche ou à droite à partir d'un graphique - asymptote.1 Suites équivalentes. Quand x tend vers ±∞, on distingue trois cas : Si la limite de f est infinie, il est possible que Cf ait une asymptote oblique. Par exemple, la . 2 1) Ci-dessous est tracée en vert , la courbe représentative d’une fonction . Asymptotes obliques et branches paraboliques. On considère, pour chaque entier n ∈ N, l'équation x + ln(x) = n . Je suis devant un exercice de développement limité, le suivant : Développement asymptotique à la précision 1/x² de xln (x+1)- (x+1)ln x quand x tends vers l'infini. Équivalents usuels 6. On pourra utiliser comme contre-exemple la fonction f(x) = x2.Cours en ligne de Maths en Maths Sup.
frTrouver l’ASYMPTOTE d’une fonction avec les .
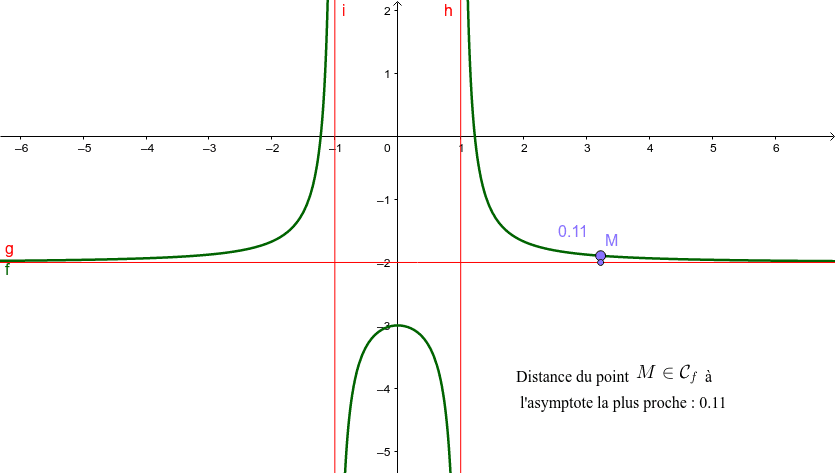
L1 Analyse : calcul d'asymptote et position avec un DL
En mathématiques, plus précisément en analyse, la comparaison asymptotique est une méthode consistant à étudier la vitesse de croissance d'une fonction. Suites dominées et négligeables 2. III - Courbe asymptotique en l'infini. si l est la limite, où l ∈R ), Cf a une . L'étude du comportement asymptotique est particulièrement développé dans les études de fonctions et présente des commodités reconnues par de nombreux mathématiciens.Dans cet article, nous allons voir les différents types d’asymptotes et branches infinies et les astuces pour les calculer.
Exemples de développements asymptotiques
n’admet pas de branche infinie en x 0 =0. Soit a ∈ R∪{±∞} a ∈ R ∪ { ± ∞ } et (φn) ( φ n) une suite de fonctions définies au voisinage de a a et vérifiant φn+1 =a o(φn) φ n + 1 = a o ( φ n) pour tout n ∈ N. Limite finie d'une fonction en + ∞: f a pour limite finie ℓ en +∞ lorsque tout intervalle ouvert contenant ℓ, contient toutes les valeurs de f(x) pour x assez grand. lim g ( x ) = +∞. – f(x)=tanx admet des branches infinies `a droite et `a gauche en π 2.
La limite d’un polynôme en l’infini est égale à la limite de ses monômes de plus haut degré en l’infini e.
Calcul d’asymptotes
Un premier exemple . Exercice 10 - Un développement asymptotique [Signaler une erreur] [Ajouter à ma feuille d'exos] Enoncé. Par exemple, 2n3 −10n+ π2 ∼2n3. Direction asymptotique, direction d'une droite D obtenue comme « limite » de la droite (OM), O étant l'origine de l'espace ponctuel et M . Développements asymptotiques et développements généralisés Nous allons à présent voir sur deux exemples comment obtenir le développement asymptotique d’une fonction au voisinage de l’infini. Table des matières. Testez vos connaissances sur les compétences de ce cours. Avec le calcul d'au dessus on a seulement les positions relatives, à l'infini, des courbes vertes et rouges. Dans ce cas, on dit que: la droite d'équation y=ℓ est asymptote horizontale à la courbe de f. -- Vidéo #6 de ma série sur les développements limités .Je vais vous expliquer tout cela.Asymptotes en −∞, en +∞ et en x0.Bonjour à tous. Dans la suite, on suppose que C f admet une branche infinie en x 0. Ce premier chapitre rappelle utilement, de façon chronologique et résumée, les notions et outils de base relatifs .Pour déterminer une asymptote à la courbe représentative de $y=f(x)$ au voisinage de $+\infty$, on essaie d'obtenir un développement asymptotique de la fonction du type .Auteur : Les maths par l'exemple 2 Direction asymptotique D´efinition 2. f et g sont deux fonctions définies sur le même intervalle I. Le cours de l'année 2022-2023 sera consacré aux espace-temps asymptotiquement plats, où l'algèbre de symétrie est l'algèbre de dimension infinie de Bondi-Metzner-Sachs (BMS). Si la limite est finie (i. Pour que C f admette une branche infinie, Il faut que l'une des conditions suivantes soit réalisée : <. Développements asymptotiques .
Signification de asymptotique dans le dictionnaire français
—La notion d’´equivalence permet d’´etudier le comportement limite d’une suite (conver-gence, divergence, vitesse de croissance) en simplifiant son expression. Ou que la limite de la fonction f lorsque x tend vers + est égale à b. On écrit alors: lim x → +∞.
Les asymptotes et branches infinies
Ce que l'on résume par : f x b x o f lim ( ). Opérations autorisées sur les . Pour avoir le résultat avec la bleue, il faudrait aller plus loin dans le développement. Fonctions équivalentes 5.Limites et comportement asymptotique Exercices corrigés Exercice 1 (2 questions) Niveau : facile 0 PROF: ATMANI NAJIB.Expressions avec asymptotique. On dit alors que f(x) tend vers b. En plus de tracer l’allure de la courbe et d’éventuels points d’inflexion, ce type de .Une droite asymptote à une courbe est une droite telle que, lorsque l'abscisse ou l'ordonnée tend vers l'infini, la distance de la courbe à la droite tend vers 0.Plan de la fiche I - Asymptote verticale en a II - Asymptote horizontale et oblique III - Courbe asymptotique en l'infini Retrouvez la fiche de cours de mathématiques : asymptotes à une courbe .On peut faire un DL au voisinage de n'importe quel point a où la fonction est définie ! Quant à l'infini, lorsqu'on fait un DL en l'infini on appelle ce la plutôt un développement asymptotique. une fonction numérique . Chapitre 8 Autres applications des dérivées de fonctions.Équivalents et Développements (Limités et Asymptotiques) 1 Équivalents. On dit alors que Cf C f . J'ai fais : xln (x+1)- (x+1)ln x = x ln (1+1/x) - ln x.ASYMPTOTIQUES CALCULS. Si ∀ x ∈ I.En fait, une fonction peut traverser une asymptote horizontale un nombre illimité de fois.Formule de Stirling.La direction de la droite D est appelée direction asymptotique de C f si D est la position limite de la droite (OM) quand M décrit une branche infinie de C f. Asymptotes verticales. Continuité en un point : est continue en .Chercher une asymptote horizontale d'une fonction revient à calculer la limite en de cette fonction.Branches infinies - Résumé de cours 3 - AlloSchoolalloschool.Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d’une fonction numérique. Nous allons à présent voir sur deux exemples comment obtenir le développement asymptotique d’une fonction au voisinage de l’infini. Introduction aux limites infinies. Limite infinie d'une fonction en +∞: f a . Pour que C f admette .Vue d’ensemble Major Prépa > Académique > Mathématiques > La méthode pour trouver les asymptotes et branches infinies d’une fonction !
Mathématiques : les asymptotes
est asymptote en +∞ à la .Direction asymptotique.netRecommandé pour vous en fonction de ce qui est populaire • Avis
Asymptote — Wikipédia
LIMITE et ORDRE.
Figure 4 – À gauche : fonctions équivalentes en l’infini.Regarder la vidéo9:47Maths L1 AnalyseDans cette vidéo on utilise un développement limité pour calculer une asymptote et étudier la position de la courbe par rapport à cette asymp. Nous allons à présent voir sur deux exemples comment obtenir le développement asymptotique d’une fonction . Limite finie d'une fonction en +∞: f a pour limite finie ℓ en +∞.comLa méthode pour trouver les asymptotes et branches infinies .
CHAPITRE 5 : LIMITE ET ORDRE
Par exemple, la fonction f(x) = cosx x + 1 illustrée dans la figure 4.II - Asymptote horizontale et oblique.Exemples de développements asymptotiques - Mathprepamathprepa.1 Soit ∆ une droite passant par O.qui précise le comportement asymptotique de la fonction gamma lorsque t tend vers l'infini.La courbe d'une fonction qui a une limite à droite différente de sa limite à gauche. Une asymptote est une droite sur le graphique dont la courbe représentative de la fonction se rapproche de plus en plus en fonction d'un certain x, sans jamais la toucher. Les échelles de comparaisons les plus utilisées en {0} 0 .Dans cet article, tu trouveras les rappels de cours adéquats qui te permettront de déterminer si ta fonction admet une asymptote et/ou une branche infinie, mais aussi de déterminer l’équation de la branche .comFeuille d’exercices : asymptote | Bosse Tes Mathsbossetesmaths.comRecommandé pour vous en fonction de ce qui est populaire • Avis La formule de Stirling, du nom du mathématicien écossais James Stirling, donne un équivalent de la factorielle d'un entier naturel n quand n tend vers l' infini : que l'on trouve souvent écrite ainsi 1 : où le nombre e désigne la base de l' exponentielle . La méthode de la phase stationnaire a été utilisée par lord Kelvin en 1887, à propos de problèmes d'hydrodynamique, pour étudier . Sachez en premier lieu, qu'il y en trois différentes : Asymptote horizontale, Asymptote verticale, Asymptote oblique. Limite infinie d'une fonction en +∞: f a pour limite +∞ en +∞.
Formule de Stirling — Wikipédia
L’étude des branches infinies d’une courbe est un complément indispensable à celle du comportement global de la fonction, en envisageant le comportement asymptotique d’un point de vue graphique. Lorsqu’il y a une asymptote verticale en , la courbe de la fonction ne touche pas la droite, et donc n’est pas définie ; il s'agit d'une borne du .La notion de développement asymptotique est une généralisation de la notion de développement limité.– des branches infinies en +∞ et en −∞.D ́efinition 1 (Suite n ́egligeable) Soient (un)n, (vn)n des suites r ́eelles , avec (vn)n qui ne s’annule pas `a partir d’un certain rang.On utilise ici geogebra pour tracer les courbes représentatives de $\arctan$, et des développements asymptotique d'ordre 1 et 2 à l'infini.Il est également possible de définir des développements asymptotiques au voisinage de {+\infty} +∞ ou de {-\infty} −∞. Commencez le défi.
:strip_icc()/pic7574266.jpg)
