Bcc cubic unit cell
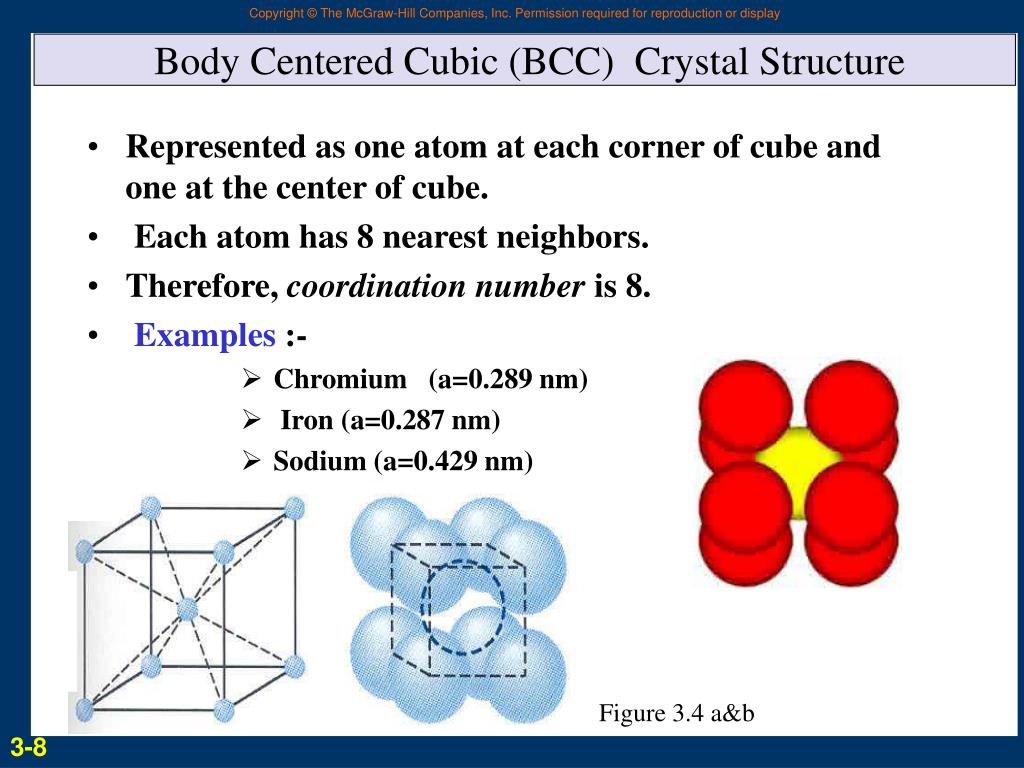
Body centered cubic
Body-Centered Tetragonal has 2 atoms per unit cell and Coordination Number CN = 8 to 12 (with a “perfect” CN= 10).For now, we will focus on the three cubic unit cells: simple cubic (which we have already seen), body-centered cubic unit cell, and face . The lengths of the edges of the unit cells are indicated by a, b, and c, and the angles are defined as follows: α, the angle between b and c; β, the angle between a and c; and γ, the angle between a and b.This basic repeating unit is called a unit cell. The conventional . The body-centered cubic (bcc) unit cell of iron and tungsten. We are going to focus on the 6 crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, hexagonal, and cubic and how to describe the unit cell, the primitive lattice vectors, and interaxial angles.Some metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and an atom in the center, as shown in Figure 2.There are three cubic lattices: simple cubic (SC), body-centered cubic (BCC), and face-centered cubic (FCC). The simple cubic has a sphere at each corner of a cube.
For the conventional unit cell a cubic one is chosen because it represents the symmetry of the .In this paper, the orthotropic mechanical properties of a BCC lattice unit cell with waved struts have been studied by means of numerical FEM simulations.For now, we will focus on the three cubic unit cells: simple cubic (which we have already seen), body-centered cubic unit cell, and face-centered cubic unit cell —all of which are illustrated in Figure 10.
Diamond Cubic Unit Cell
This is called a body-centered .
What is a Unit Cell?
The face-centered cubic (fcc) unit cell of aluminium and copper.
What Does BCC Stand For?
Body-centred cubic – bcc: Interactive 3D Structure.6: The General Features of the Seven Basic Unit Cells.Atoms on the corners of the unit cell count as ⅛ of an atom, atoms on a face count as ½, an atom in the center counts as a full atom.Volume occupied by the atoms per unit cell (v) Volume of unit cell for a cubic system (V) = a 3.
Primitive Unit Cells (including Wigner
These are corner atoms, so each one only contributes one eighth of an atom to the unit cell, .However, not one of the lattice points uniquely belongs to any primitive cell shown in Figure 1.
Cubic Unit Cells
To be able to .
Temps de Lecture Estimé: 9 min Hence, the packing factor is 0.
For example, you know that the BCC unit cell has 2 atoms per cell in the traditional way of drawing the cell.The body-centered cubic (bcc) lattice ( Figure 1.Co-ordinates are converted to fractional co-ordinates by dividing by the respective cell-dimension - for example, a point (x,y,z) in a unit cell of dimensions a x b x c has fractional co-ordinates of (x/a , y/b , z/c).
The diagonal through the body of the cube is 4x (sphere radius).A unit cell can either be primitive cubic, body-centred cubic (BCC) or face-centred cubic (FCC). (Note that there are actually seven different lattice systems, some of which have more than one type of lattice, for a total of 14 different types of unit cells.In a single cell, each corner contains an eighth of each atom. A BCC unit cell contains two atoms: one-eighth of an atom at each of the .
Cubic crystal system
Some metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and an atom in the center, as shown in Figure 2. Atoms in the corners of a BCC unit cell do not contact each other but contact the atom in the center. Since there are eight corners, the total amount of atoms in the simple cubic cell is one (the cell is a proper unit cell). The hexagonal closest packed (hcp) has a coordination number of 12 and contains 6 atoms per unit cell. Many metals, like aluminium, copper, or nickel, crystallize into the fcc lattice.For now, we will focus on the three cubic unit cells: simple cubic (which we have already seen), body-centered cubic unit cell, and face-centered cubic unit cell —all of which .BCC: Unit Cell Type: Cubic: Cubic: Relationship Between Cube Edge Length a and the Atomic Radius R: a = 2R√2: a = 4R/√3: Close-Packed Structure: Yes: No: Atomic Packing Factor (APF) 74%: 68%: Coordination Number: 12: 8: Number of Atoms per Unit Cell: 4: 2: Number of Octahedral Interstitial Sites: 4: 6: Number of Tetrahedral . (part (b) in Figure 12.Download scientific diagram | Unit cells of bulk (A) face centered cubic (FCC), (B) body centered cubic (BCC) and (C) hexagonal closed packed (HCP) crystal structures, (D) a . Simple Cubic: 8 corner atoms × ⅛ = 1 atom/cell . The higher coordination number and packing efficency mean that this lattice uses space more efficiently than simple cubic. The face-centered cubic (fcc) has a .1 Crystallographic Directions: When discussing crystals we will also have to specify . There is an atom at each corner of the cube, similar to the simple cubic structure. Any atom in this structure touches four atoms in the layer above it and four atoms in the layer below it.Body-centered Cubic Unit Cells. In a body-centered cubic .The simple cubic has a sphere at each corner of a cube. In this section, we will discuss the three types of unit cell in detail. However, there is also another atom at the centre of the cube .Let's analyze them in detail! The simple cubic lattice.As the name itself suggests, the body centred cubic structure has a cube-shaped unit cell.
Body Centered Cubic (bcc)
8, a simple cubic lattice of anions contains only one kind of hole, located in the center of the unit cell.The simple cubic (SC) unit cell can be imagined as a cube with an atom on each corner.
Body Centered Cube (BCC):
Because the volume of the unit cubic cell is a 3, and each unit cell has two lattice points, the primitive cell of the bcc lattice is half of the volume of the unit cell. Each sphere has a coordination number of 6 and there is 1 atom per unit cell. This unit cell is the simplest for people to understand, although it rarely . In the case of a cubic unit cell each co-ordinate will simply be divided by the cubic cell constant, a. The length of each edge is given by the lattice parameter ‘a’. Body centered cubic is both a crystal structure and a Bravais lattice and has one atom in the basis. There is an atom at each .The face-centered cubic unit cell contains a single octahedral hole within itself, but octahedral holes shared with adjacent cells exist at the centers of each edge. This misconception is easy to make, since there is a center atom in the unit cell, but CsCl is really . Na, K and Cr form this crystal structure. Using this, let's calculate the number of atoms in a simple cubic unit cell, a face centered cubic (fcc) unit cell, and a body centered cubic (bcc) unit cell. These are types of atom arrangements. BCC stands for Body-Centered cubic unit cell, while FCC stands for Face-centered Cubic unit cell.The diamond cubic crystal structure is based on the face-centered cubic Bravais lattice (you can imagine it as two FCC unit cells, offset by ¼).The lattice constants of bcc lattices at low temperatures are shown in Table 1. Related Structure: Caesium chloride (CsCl) 268. As shown in part (a) in Figure 12.3D-view of the bcc-structure: Conventional unit cell, primitive unit cell and Wigner-Seitz cell. There are 8 atoms per unit cell, and each atom is tetrahedrally coordinated so that it has 4 nearest neighbors. In the figure above, the grey grid shows the outline of the unit cell, while each circle represents an atom. Body-centered Cubic (BCC) unit cells indicate where the lattice points appear not only at the corners but in the center of the unit cell as well. Axial and shear relative properties have been obtained for different .Common Structures of Binary Compounds. In a bcc arrangement, a unit . For now, we will focus on the three cubic unit cells: simple cubic (which we have already seen), body-centered . As a second example, let us turn to another lattice type: the body-centered cubic (bcc) lattice. In BCC, the structure consists of various atoms arranged or packed in a cubic lattice where each or every single corner or edge of the cube/cubic shares a single atom with the atom in the . Each of these twelve edge-located sites is shared with four adjacent cells, and thus contributes (12 × ¼) = 3 atoms to the cell.Most metal crystals are one of the four major types of unit cells. Because this hole is equidistant from all eight atoms at the corners of the unit cell, it is called a cubic hole.The BCC unit cell has an atom at each corner of a cube, and another atom at the center of the cube. Conventional Unit Cell. If there are components in the center of each face in addition . Here, 74% volume of the unit cell of a simple cube is occupied by atoms, and the remaining 26% volume is vacant.This Demonstration lets you visualize and explore four different cubic crystal lattices: simple cubic (sc), body-centered cubic (bcc), face-centered cubic (fcc), and the diamond lattice .A unit cell is the smallest representation of an entire crystal.
The body centred cubic structure (bcc)
You may see BCC in the context of either: BCC crystal structure.3 Crystal Systems: Simple Cubic, BCC, FCC, HCP.Body-centered Cubic. The unit cells stack together like this: We can also . For the atoms along the corners of the unit cell, each atom is shared amongst eight neighboring cells, so each cell contains \(1 / 8\) of an . Cubic: a = b=c, alpha= beta=gamma = 90 degrees.The body centred cubic structure (bcc) As the name itself suggests, the body centred cubic structure has a cube-shaped unit cell. In the simple cubic lattice, each atom sits at a corner of a cube. Thus, an atom in a BCC structure has a coordination number of eight.List of Space Groups. All crystal lattices are built of repeating unit cells. For now, we will focus on the three cubic unit cells: simple cubic (which we have already seen), body-centered cubic unit cell, and face-centered cubic unit cell—all of which are illustrated in Figure 11. Let us start with aluminium . This is the lattice of many transition metals, like iron (Fe) or . A cubic unit cell has been considered, characterized by a sinusoidal shape for the struts with different wave amplitudes.Cubic unit cells of metals show (in the upper figures) the locations of lattice points and (in the lower figures) metal atoms located in the unit cell.In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. The body-centered cubic (bcc) has a . The packing efficiency of a bcc lattice is considerably higher than that of a simple cubic: 69. Thus, the unit cell of .A BCC unit cell contains two atoms: one-eighth of an atom at each of the eight corners ( atom from the corners) plus one atom from the center.
Atoms in the corners .
This page is going to discuss the structure of the molecule cesium chloride ( CsCl CsCl ), which is a white hydroscopic solid with a mass of 168. In a body-centered cubic (bcc) arrangement of atoms, the unit cell consists of eight atoms at the corners of a cube and one atom at the body center of the cube.
This is one of the most common and simplest shapes . This is called a body-centered cubic (BCC) solid.
