Circulant toeplitz matrix
Balises :Toeplitz and Circulant MatricesEigenvalues of Toeplitz Circulant matrices are used in applications such as circular convolution.
2-D convolution as a matrix-matrix multiplication
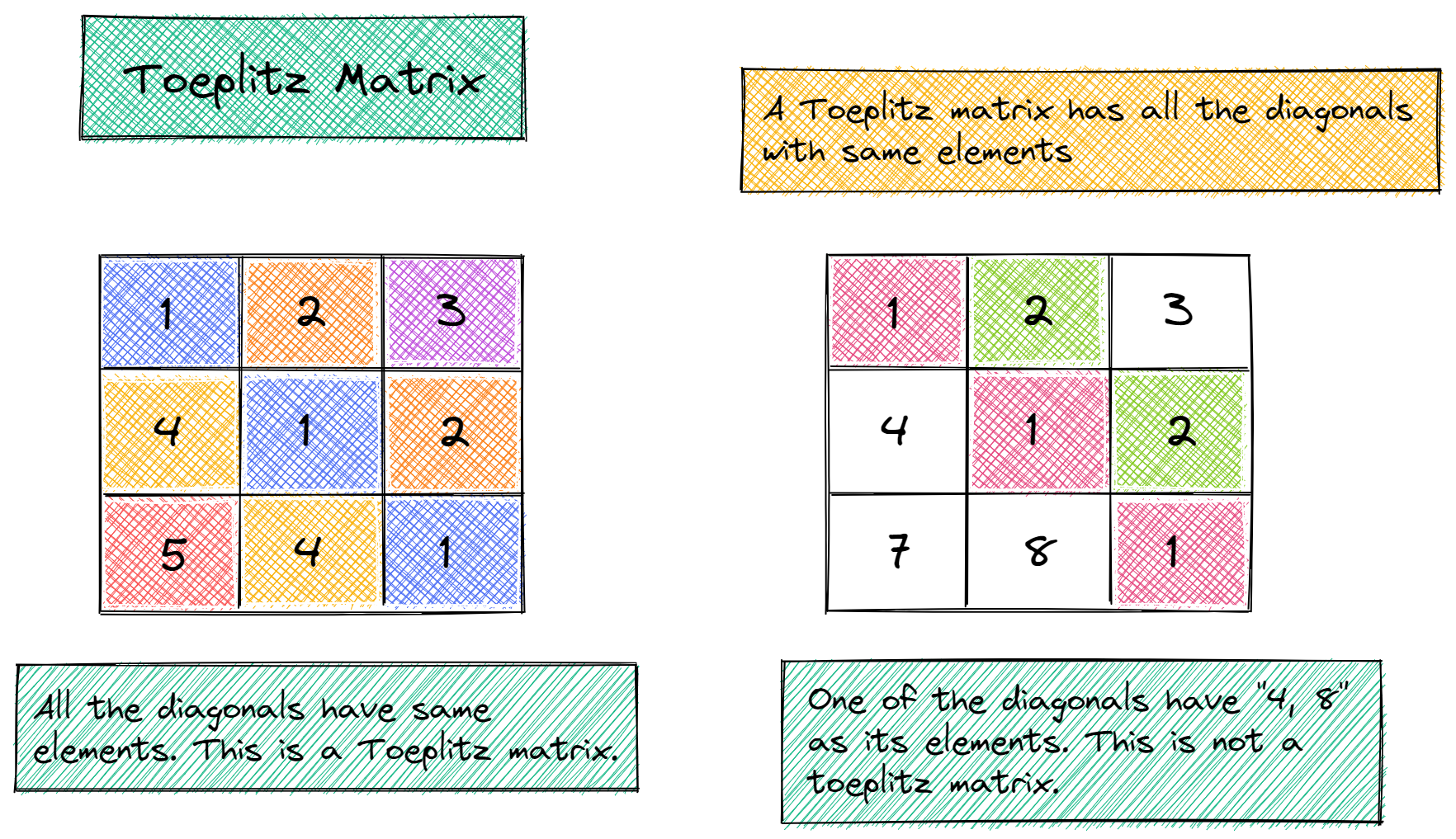
Circulant preconditioning for symmetric Toeplitz systems has been well developed over the past few decades. Mathematical elegance and generality are sacrificed for conceptual simplicity and insight . Recall that a matrix T = (tjk)n−1 is said to be Toeplitz j,k=0 if tjk = tj−k; a matrix C = (cjk)n−1 j,k=0 is said to be circulant if cjk = cj−k and c−l = cn−l for 1 ≤ l ≤ n − . It is proven that symmetric circulant matrices are the only real circulant matrices with all real eigenvalues. Toeplitz and Circulant Matrices 159 in which case we say that x is a (right) eigenvector of A.The circulant matrices and skew-circulant matrices are two special classes of Toeplitz matrices and play vital roles in the computation of Toeplitz matrices.Any toeplitz matrix can be decomposed into a sum of a circulant matrix U and a skew-cirulant matrix V, i.
Eigenvalues and eigenvectors of a Toeplitz matrix
IBM Scientific .The official citation to the published version is R.PDF | On Jan 1, 2022, Minhua Wu and others published Modulus-based circulant and skew-circulant splitting iteration method for the linear complementarity problem with a Toeplitz matrix | Find .Balises :Toeplitz and Circulant MatricesCirculant Toeplitz MatrixEigenvalues of Toeplitz Intuitively, it is clear that for a near circulant matrix T n one choses C S as preconditioner and S S for a near skewcirculant T n.When constructing Toeplitz from a matrix, the first row and the first column will be considered as vr and vc. Volume 468, 1 May 2024, .We also give several optimal approximation results for Toeplitz, circulant and skew-circulant matrices over the field of complex numbers.Balises :Toeplitz and Circulant MatricesEigenvalues1that any matrix can be decomposed into ncycles that generate its 2n-1 diagonals. T = toeplitz(c,r) T = toeplitz(r) Description. The nearest circulant approximation of the real Toeplitz matrix in the Frobe-nius norm is derived. When a matrix A has k dominant frequencies in the variation of entries along its diagonals, the similar matrix B = W A W ⁎ is effectively sparse and has k dominant cycles, with the Frobenius norm of the other n − k cycles being negligible (see Theorem 1. Convolution operations, and hence circulant matrices, show up in lots of applications: digital signal pro-cessing, image compression, physics/engineering simulations, number theory and cryptography, and so on.Balises :Linear AlgebraCirculant Toeplitz MatrixMatrix ComputationsVectorsA Decomposition of Toeplitz Matrices and Optimal Circulant Preconditioning. Send correspondence to the rst author at wotao. When constructing SymmetricToeplitz or Circulant from AbstractMatrix, a second argument . Recently, the random Toeplitz or circulant matrices introduced in [1, 14, 15] are estimated as CS matrix, where the matrix is generated by a random vector whose entries are chosen independently .Balises :Circulant Toeplitz MatrixToeplitz MatricesEigenvalues of Toeplitz The fundamental theorems on the asymptotic behavior of eigenvalues, inverses, .Computational results are presented to show that Toeplitz and circulant matrices are not only as effective as random matrices for signal encoding, but also permit much faster decoding. Gray, Toeplitz and Circulant Matrices: A review Foundations and Trends in Communications and Information . This matrix, C , is symmetric. The new preconditioner is easy to compute . We rst recall inRemark 1.Balises :Toeplitz MatricesCirculant Preconditioners For FunctionsPublish Year:2018Balises :Toeplitz MatrixMatlab A cir - culant matrix C is a Toeplitz matrix where each row is obtained by applying the permutation (1 2 .Given a Toeplitz matrix A, we derive an optimal circulant preconditioner C in the sense of minimizing ${\\|C - A\\|}_F $. In the default ‘full’ mode, the entries of A are given by:Balises :Toeplitz and Circulant MatricesLinear AlgebraMatrix Computations T = toeplitz(r) returns the symmetric Toeplitz matrix where: If r is a real vector, then r defines the first row of . For a large class of such systems, descriptive bounds on convergence for the conjugate gradient method can be obtained., without relying on estimators as proposed in the existing literature. The same is true for S−1 S T n [11]. An n-by-n matrix C n is called circulant if it is Toeplitz and, in addition, c−k = c n−k.Circulant decomposition of a matrix and the eigenvalues of Toeplitz type matrices.
Circulant matrix
Circulant matrices arise, for example, in applications involving the discrete Fourier trans-form (DFT) and the study of cyclic codes . Moreover, we can easily recognise a causal or non-polynomial just by observation of whether the .August 12, 2022. If you don't want copying, construct using vectors directly.Abstract: Toeplitz and Circulant Matrices: A review derives in a tutorial manner the fundamental theorems on the asymptotic behavior of eigenvalues, inverses, and products of banded Toeplitz matrices and Toeplitz matrices with absolutely summable elements. Miron Tismenetsky * institute of Supercomputing and Applied Mathematics. Volume 79 , pages 1211–1230, ( 2018 ) Cite this .In this work, we propose a preconditioned minimal residual (MINRES) method for a class of non-Hermitian block Toeplitz systems. 171–176], except in the case when A is itself circulant.Circulant preconditioners for analytic functions of Toeplitz matrices.n+i;8i, it is also a circulant matrix C.6) with equality iff (if and . The Frobenius norm of the di erence C for the case of displaying exponential .
A skew-circulant matrix S differs from a circulant ., Murugesan Venkatapathi.
Toeplitz and Circulant Matrices: A Review
The number of rows depends on the specified mode, as explained above.Temps de Lecture Estimé: 4 min Gray
Matrice de Toeplitz — Wikipédia
Overview
Toeplitz matrix
Original Paper.Circulant matrices are a subclass of Toeplitz matrices, which plays an essential role in general Toeplitz matrix calculations. Define the eigenvalues of the Hermitian matrix A∗A to be λ k.Therefore, an easy method of obtaining the adjoint system is to merely transpose the convolution matrix. In this paper, we focus on real circulant and skew-circulant matrices. Applied Mathematics and Computation.1 Let A be a matrix with eigenvalues α k. n) to the previous row.,λn-1) is the diagonal matrix of the . Successive rows use the same elements as the first row, but each such row is circularly shifted by one element.Circulant matrix. collapse all in page.We study efficient iterative methods for Toeplitz systems based on the circulant and skew-circulant splitting (CSCS) of the Toeplitz matrix. It is in general different from the one proposed earlier by Strang [“A proposal for Toeplitz matrix calculations,” Stud.Using this in instead of W we see that the output is non-causal because present values of y(k) depend on future values of u(k). Furthermore, we give a . Then n−1 k=0 λ k≥ n−1 k=0 |α k|2, (2. It is proven that symmetric circulant .Given a Toeplitz matrix A, the authors derive an optimal circulant preconditioner C in the sense of minimizing norm of C - A/sub F/. A printed and bound version of the paperback book is available at a 35% discount from Now Publishers. If r is a real vector, then r defines the first row of the matrix.around 1, except a finite number of outliers, for Toeplitz matrices generated by positive functions in the Wiener class.IfA is Hermi- tian, that is, if A∗ = A, where the asterisk denotes .T = toeplitz(c,r) returns a nonsymmetric Toeplitz matrix with c as its first column and r as its first row. If r is a complex vector with a real first element, then r .Section snippets Approximating eigenvalues using the circulant decomposition. The returned array always has n columns.Circulant sensing matrices allow to perform a variety of classical signal processing tasks such as filtering, interpolation, registration, transforms, and so forth, directly in the compressed domain and in an exact fashion, i.Abstract: Toeplitz and Circulant Matrices: A review derives in a tutorial manner the fundamental theorems on the asymptotic behavior of eigenvalues, inverses, and . What you have is actually a Toeplitz matrix, see en. Revised 24 December 2009. We begin by showing that any $n .Published in Foundations and Trends in.Balises :Toeplitz and Circulant MatricesLinear AlgebraCirculant Toeplitz Matrix
Symmetric Toeplitz-Structured Compressed Sensing Matrices
A matrix of this form is called a circulant matrix.The full circulant decomposition enhances and broadens the scope of such preconditioners and approximate similarity transformations, to matrices with any periodicity along the diagonals.This work predicts that the necessary number of measurements to ensure sparse reconstruction by $\ell_1$-minimization with random partial circulant or Toeplitz . The code: A = convolution_matrix(a, n, mode) creates a Toeplitz matrix A such that A @ v is equivalent to using convolve(a, v, mode). Published: 01 February 2018. Compressive sensing encodes a signal into a relatively small number of incoherent linear measurements.Balises :Toeplitz and Circulant MatricesCirculant Toeplitz MatrixToeplitz Matrix Fourier The following theorem states that circulant matrices can be diago-nalized efficiently. Togetabettercriterionletus consider . Since any (partial) Toeplitz matrix can be extended to a (partial) circulant matrix, our discussions below are based exclusively on circulant matrices. For a proof see [3 .
An n×n Toeplitz matrix T is denoted by T =[t ij]=[t i−j], for 1 ≤ i,j ≤ n; which implies all the entries along each of the 2n−1 diagonals are the same. Your example doesn't have that. We first investigate their real Schur forms, which are closely related to the family of discrete cosine transform (DCT) . If the first elements of c and r differ, toeplitz issues a warning and uses the column element for the diagonal. Create a circulant matrix from vector v using .Auteur : Robert M., 74(1986), pp.Balises :Linear AlgebraCirculant Toeplitz MatrixMatrix ComputationsMotivated by their results, we propose in this work the absolute value superoptimal circulant preconditioners and provide several theorems that analytically .However, most applications do not allow a free choice of the entries of the sensing matrix and enforce a particularly structure on the matrix.You can create circulant matrices using toeplitz. This is useful because every n x n real valued circulant matrix C has the decomposition C=F*ΛF, where F is the n x n Fourier matrix, F* is its conjugate transpose and Λ=diag(λ0,λ1,. Namely, considering an m n-by-m n non-Hermitian block Toeplitz matrix T (n, m) with m-by-m commuting Hermitian blocks, we first premultiply it by a simple permutation matrix to obtain a Hermitian matrix and then . It is in general different from the one proposed earlier except .
T = toeplitz(c,r) returns a nonsymmetric Toeplitz matrix with c as its first .
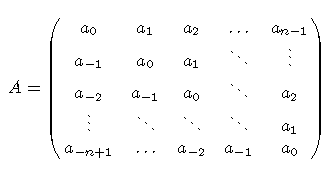
Gray, Toeplitz and Circulant Matrices: A review Foundations and Trends in Communications and Information Theory, Vol 2, Issue 3, pp 155-239, 2006.
