Coefficient of variation explained
r 2 = R 2 = η 2.R-squared or coefficient of determination.
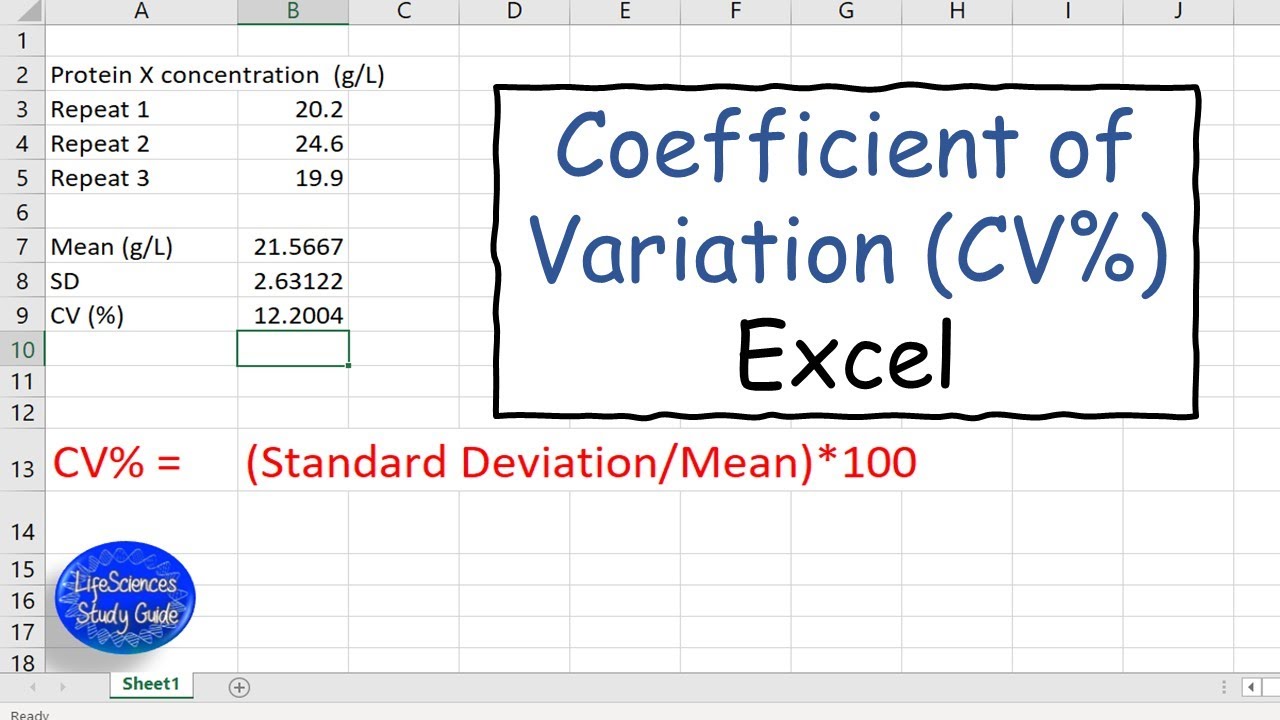
The coefficient of variation (Cᵥ) is the ratio of the standard deviation to the mean, sometimes expressed as a percentage.5, which sits in front of the variable . It is calculated as: CV = σ / μ. However, this variable is correlated with another variable that also explains a portion of the total variance. Depending on the context of the application, you can make slight changes to this formula.Auteur : Wrath of MathYoutube Link: http://www. The maximum is the largest value in the dataset and the minimum is the smallest value. For example, let’s calculate the coefficient of variation given a standard deviation of 0.The coefficient of variation (CV) is a statistical measure of the relative dispersion of data points in a data series around the mean.Rice University. Distinguish between ω2 ω 2 and .The coefficient of variation is a statistical measure used to assess the variability of a data set relative to its mean. The higher the coefficient of variation, the greater the level of . μ: The mean of dataset. σ = Standard Deviation. It provides a dimensionless measure, allowing for a direct comparison of variation between datasets that might have .Learn Statistics - All about Statistics In plain English, the coefficient of variation is simply the ratio between the standard deviation and the . In other words, the coefficient of determination tells one how well the data fits the model (the goodness of fit). This equation can also be applied to sample data, where s is used for the standard deviation and x̅ for the mean: Cᵥ = (s/x̅) × 100%.When linear regression is used, R2, also called the coefficient of determination, is a preferred and arguably the most often reported metric gauging the . Intuitively, if the mean is the expected value, then the coefficient of variation is the expected variability of a measurement .Please like and subscribe, and also click the bell notification.Coefficient Of Variation Formula Explained. Explained variance can be denoted with r 2.
You can interpret the coefficient of determination (R²) as the proportion of variance in the dependent variable that is predicted by the statistical model. In simple terms, the Coefficient of Variation is 100 times of Coefficient of Standard Deviation. The coefficient of variation is a statistical measure used to assess the variability of a data set relative to its mean. Mathematically, the . How can I account for this covariance? For example: Total variance explained = 95%, i.What is the Coefficient of Variation? The coefficient of variation (relative standard deviation) is a statistical measure of the dispersion of data points around the mean.Photo by Josh Rakower on Unsplash. If you have a correlation coefficient of 1, all of the rankings for each variable match up for every data pair. Compute η2 η 2 Compute ω2 ω 2.That makes the coefficient of variation a measure of relative variability, so the relative variability of lengths may be compared with that of weights, and so forth.In simple terms, the coefficient of variation is the ratio between the standard deviation and the mean.The coefficient of multiple determination is the proportion of variation in the dependent variable that can be explained by the multiple regression model based on the . a time series) in that it is a proportion (and therefore can be expressed as a percentage). To express CV in percent form, multiply by 100, then add a percent symbol (%).
One way to measure the effect of conditions is to determine the proportion of the variance among subjects' scores that is attributable to conditions.
Coefficient de variation — Wikipédia
Explained Variance / Variation
How to interpret the coefficient of variation?
The coefficient of variation is often expressed as a percentage.Understanding Coefficient of Variation: A Comprehensive Guide in Intro Stats / AP Statistics. R2 R 2 is a measure of how well the values of y y are explained by x x.Explained variation.Statistics Tutorials.
SEy is the total variation in y (sum of squared distances from the mean of y) and .Higher percentages of explained variance indicates a stronger strength of association.
Coefficient of Determination (R²)
When linear regression is used, R 2, also called the coefficient of determination, is a preferred and arguably the most often reported metric gauging the model’s goodness of fit. Interquartile range (IQR) Variance and Standard Deviation. where: σ: The standard deviation of dataset.The coefficient of determination \(r^{2}\), is equal to the square of the correlation coefficient. In statistics, explained variation measures the proportion to which a mathematical model accounts for the variation ( dispersion) of a given data set. It is expressed as a percentage and is calculated by dividing the standard deviation of the data by the mean and multiplying by 100 .It is commonly used to quantify goodness of fit in statistical modeling, and it is a default scoring metric for regression models both in popular statistical . You could also think of it as how much closer the line is to any given point when compared to the average value of y. Measures of Variability: Coefficient of Variation, Variance, and Standard Deviation. 1: Distribution of leniency scores.
Coefficient of Variation Meaning and How to Use It
Coefficient of Determination Calculator
The question is how this variance compares with what the variance would have been if . In linear regression, r-squared (also called the coefficient of determination) is the proportion of .Vue d’ensemble783 and a mean of 23.A coefficient of variation, often abbreviated as CV, is a way to measure how spread out values are in a dataset relative to the mean.Glossary:Coefficient of variation - Statistics Explained . The × 100% is only used when expressing Cᵥ as a percentage.The calculus of variations (or variational calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima .
:max_bytes(150000):strip_icc()/Coefficient-of-Variation-V2-9df0f99589de4c428135b4954ccf972d.jpg)
Coefficient of variation is the standard deviation divided by the mean; it summarizes the amount of variation as a percentage or proportion of the total.The coefficient of variation is a measure of relative dispersion. For example, there is some variability in the dependent variable values, such as grade.
Coefficient of Variation, Variance & Standard Deviation
= the difference between the x-variable rank and the y-variable rank for each pair of data. where σ is the standard deviation of a population, and μ is the mean.Overview
Coefficient of Variation
- Cross Validatedstats. = sum of the squared differences between x- and y-variable ranks. we should realize that if we have a significant correlation, the stronger that correlation is between our x x and y y, the more we can account for the .Coefficient of Variation is expressed in terms of percentage and can be determined using the following formula: Where, C.The coefficient of determination R2 R 2 (or r2 r 2) is the fraction (or percent) of the variation in the values of y y that is explained by the least-squares regression of y y on x x. Google Classroom. It represents the ratio of.It describes the standard deviation as a percentage of the arithmetic mean. The range is the difference in the maximum and minimum values of a data set.Regarder la vidéo3:42The coefficient of variation is the standard deviation divided by the mean.The coefficient of determination, often denoted R 2, is the proportion of variance in the response variable that can be explained by the predictor variables in a regression model. Because the mean and standard deviation have the same units, the coefficient of variation (CV) is. The standard deviation tells us that the typical value in this dataset lies 9.
Coefficient of Determination
Definition
In this example, the variance of scores is 2.Explained Variation and the Coefficient of Determination. This coefficient can be used to compare the dispersions of quantitative variables that are not expressed in the same units (for example, when comparing the salaries in different countries, given in different .
Explained Variation and the Coefficient of Determination
How To Calculate The Coefficient Of Variation (CV) - Top .
Coefficient of variation
The coefficient of determination (R² or r-squared) is a statistical measure in a regression model that determines the proportion of variance in the dependent variable that can be explained by the independent variable.Measures of Variability. It also means that you make better predictions (Rosenthal & Rosenthal, 2011).
Explained Variation and the Coefficient of Determination
The r-squared coefficient is the percentage of y-variation that the line explained by the line compared to how much the average y-explains. Simply enter a list of values for x (the predictor variable) and y (the . The distribution/series for which the . As we consider the total variation of the y y values seen in a scatterplot, given by. It is a parameter estimate describing the relationship between one of the independent variables in your model and the dependent variable. percent form = CV × 100%.We can then use these values to calculate the coefficient of variation: CV = s / x.An easy approach in finding the Coefficient of Variation. Join over 2 million students who advanced their . Coefficient of variation is effectively a normalized or relative measure of the variation in a data set, (e. In ANOVA, it’s called eta squared (η 2) and in regression analysis, it’s called the Coefficient of Determination . The higher the coefficient of variation, the higher the standard .Coefficient of Variation (CV) = (Standard Deviation/Mean) × 100. The coefficient of variation (CV) is the ratio of the standard deviation to the mean.The coefficient of variation (CV) is a standardized measure of relative risk, representing the ratio of the standard deviation to the mean, and is especially valuable when comparing the risk of two different investments or assets.A regression coefficient is the quantity that sits in front of an independent variable in your regression equation. In the simple linear regression below, the quantity 0. 8,9 R 2 is universally interpreted as the proportion or percent of the variation in the dependent variable that is explained or predicted by the independent . = Coefficient of Variation. This calculator finds the coefficient of determination for a given regression model. For example, if you want to calculate CV in financial research, you can rewrite the formula as: Coefficient of Variation = (Volatility ÷ Expected Returns) × 100%.
