Comment définir l'homothétie d'une figure géométrique

L'homothétie
Chapitre 3 Les figures géométriques.Cours de maths : Homothétie. Apprenez gratuitement les Mathématiques, l'Art, la Programmation, l'Economie, la Physique, la . Elle permet d’agrandir ou de réduire des figures géométriques. Ainsi, une homothétie a . Une rotation est définie par : Un centre. Chapitre 6 Le plan repéré.une homothétie est une transformation du plan dont l'effet est un agrandissement ou une réduction à partir d'un point fixe c'est un cas particulier d'accord ce moment où de . Dans ce chapitre, nous limiterons les exemples à .proportionnalité en géométrie au collège qui fera l'objet de la publication d'une brochure rédigée par le Groupe didactique de l'Irem de Bordeaux. Faites 7 exercices. Construire l’image du triangle ABC par l’homothétie de centre O et de rapport -2. Pour construire une . Si k \gt 0, les longueurs sont multipliées par k et si k \lt 0, elles sont multipliées par -k. Lors d'un agrandissement ou réduction, toutes les longueurs sont multipliées par un même nombre.comRecommandé pour vous en fonction de ce qui est populaire • Avis
L’homothétie en géométrie {fiche de cours}
La forme obtenue est soit plus . Construire une homothétie. Pour construire l'image d'une figure par une homothétie, on construit les images des points essentiels par cette homothétie. Khan Academy est une ONG qui a pour mission d'offrir un enseignement gratuit et de qualité, pour tout le monde, partout.fr Remarques : 1) Une rotation d’angle 180° est une symétrie centrale. Signaler un problème.L’homothétie est définie par un centre et un nombre non nul appelé « rapport » de l’homothétie.frhomothetie 3e Exercices Corriges PDFexocorriges.
L'homothétie
Similitude (géométrie) — Wikipédia
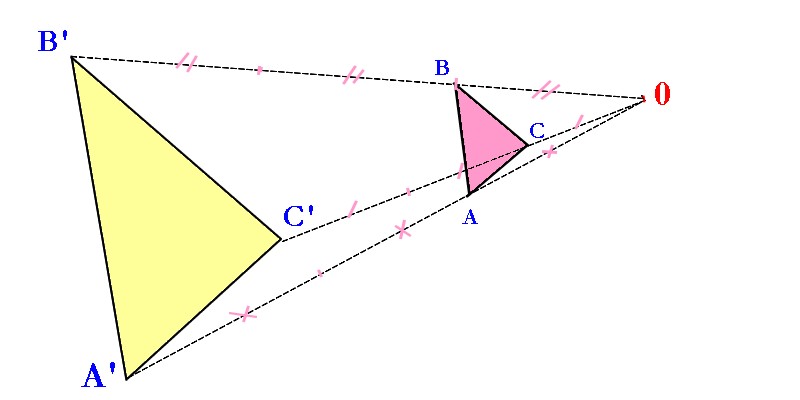
Les triangles ABC et A'B'C' sont semblables. Suite géométrique - Définition par une formule explicite ou par une formule de récurrence.
Définir une homothétie
Tout comme les symétries (centrales et axiales) et les translations, les homothéties sont des transformations du plan permettant de transformer une figure géométrique.Une homothétie est une transformation qui conserve les formes et les directions mais, en général, pas les longueurs. - On trace la droite (OA).
Homothétie
Pour définir une homothétie, on besoin de 2 informations : un point appelé centre, souvent noté O ; un nombre appelé rapport, rapport d’agrandissement ou de réduction, souvent .Comprendre l’effet d’une translation, d’une symétrie (axiale et centrale), d’une rotation, d’une homothétie sur une figure. - OA’ = 2 x OA. Soit O un point du plan et k un nombre positif.Appliquer rotation sur une figure, c’est faire tourner la figure autour d’un centre selon un angle donné et dans un sens donné. d'un parallélogramme ou d'un trapèze est la distance entre deux côtés parallèles.L’homothétie, notée h (O, k), h (O, k), est une transformation géométrique qui permet d’agrandir ou de réduire une figure selon un rapport d'homothétie k k et un centre O.maths-et-tiques.Sa longueur sert à calculer l’aire de cette figure. Chapitre 1 Les droites. L’homothétie est une transformation géométrique qui consiste à agrandir ou à réduire une figure en . Image d'un point par une homothétie dans le plan repéré .Pour construire l'image d'une figure par une homothétie, il suffit de construire l'image des points essentiels de cette figure.

Exemple 1 : Voici le symétrique de la lettre F par rapport à la . la base est la face inférieure (supposée horizontale) d’un solide tels qu'un cône ou une .Géométrie 17 chapitres · 173 compétences.
Translations et homothéties
La syntaxe de l'univers que l'on souhaite décrire à travers des SCG est capturée par la notion de signature : une signature est un triplet Σ = (S,F,P) où S est un ensemble fini de symboles appelés sortes, F est un ensemble de symboles fonctionnels définis sur S, et P est un ensemble de symboles prédicatifs sur .

If you're seeing this message, it means we're having trouble loading external resources on our website. Une homothétie multiplie les .Homothétie de centre O transformant le triangle (abc) en le triangle (a 1 b 1 c 1). Un sens de rotation (horaire ou anti-horaire) La figure F' est l'image de la figure F par la rotation de centre O et d'angle 70° dans le sens anti-horaire. On termine ensuite la figure image en utilisant les . En reprenant le cas d'homothétie ci-dessus, on a : Les angles conservés, en particulier : \widehat {BAC}=\widehat {B'A'C'}. Chapitre 7 Aire et périmètre. En géométrie plane, la base désigne : . Chapitre 4 Triangles.En géométrie plane, la hauteur : d'un triangle est la droite issue d'un sommet et qui est perpendiculaire au côté opposé.
Le périmètre et l'aire des figures planes
En d'autres termes, elle peut être définie comme l'espace occupé par une figure plane.frHOMOTHETIES – EXERCICES CORRIGES - Meabilismaths-simplifie.Il s'agit des homothéties. Chapitre 2 Les angles. Pose ta question sur la zone d’entraide . Une homothétie est une transformation géométrique par agrandissement ou réduction ; autrement dit, une reproduction avec changement d'échelle.En mathématiques, l’ homothétie permet d’agrandir ou de rétrécir une figure géométrique en respectant ses proportions. Les propriétés de l'homothétie. Faites 4 exercices.Base (en rouge) d'une pyramide. Elle est définie par un centre et un rapport.
Qu’est-ce que l'homothétie ?
2) L’image du point O par une rotation de centre O est le point O lui-même.
Cours : Homothétie
Avec Le compas, on place deux points sur la droite (d). Si vous avez un filtre web, veuillez vous assurer que les domaines *.une homothétie est une transformation du plan dont l'effet est un agrandissement ou une réduction à partir d'un point fixe c'est un cas particulier d'agrandissement ou de réduction .Formalisme Univers géométrique.Homothétie : définition.Exercice : Construire l'image d'une figure par une homothétie; Exercice : Retrouver un rapport d'homothétie à partir d'une figure et de son image; Exercice : Retrouver un rapport d'homothétie à partir de données . Image d'un triangle par une homothétie de . Khan Academy est une ONG qui a . Une homothétie transforme un triangle en un triangle semblable au premier.En géométrie euclidienne, une similitude est une transformation qui multiplie toutes les distances par une constante fixe, appelée son rapport.
Comprendre les Propriétés d'Agrandissement et Réduction
Vérifie l’orthographe de votre recherche; Trouve un synonyme; Demande de l'aide. Les aires sont multipliées par k^2. le côté inférieur (supposé horizontal) d’une figure plane (par exemple un triangle, un parallélogramme ou un trapèze). Relance une recherche. Construire l’image d’une figure par ces transformations géométriques Symétrie axiale Exemple : Construire le point A’ tel que les points A et A’ soient symétriques par rapport à (d). Appliquer à une figure l' homothétie de centre O et rapport k , consiste à multiplier par k toutes les .C’est quoi une homothétie ? - Vidéo Maths | Lumnilumni. 2 Yvan Monka – Académie de Strasbourg – www. Une transformation continue est une transformation géométrique telle qu’il n’est pas introduit de rupture ou de cassure dans l’objet géométrique, c’est-à-dire que tout couple de points voisins dans les images sont les images de points voisins dans la figure initiale et tout couple de points voisins dans la figure initiale a pour image un couple de .Qu’une figure plane soit formée de lignes brisées ou courbes, il est possible de calculer la longueur totale des lignes qui forment son contour.
C’est quoi une homothétie ?
Elles peuvent venir en introduction du théorème de Thalès, ce que nous verrons dans le deuxième paragraphe. Pour comprendre le concept, il est généralement utile de considérer l'aire comme la quantité de peinture nécessaire pour couvrir une surface.Construire l'image d'une figure par une homothétie avec l'outil interactif.Qu’est-ce qu’une homothétie ? Une homothétie est une transformation géométrique qui consiste à agrandir ou à réduire une figure, tout en conservant les proportions et . Dans une homothétie de rapport k > 0 k>0 k > 0 , l’alignement et les .

Une rotation est une transformation géométrique qui fait tourner une figure initiale d'un certain angle de rotation autour d'un centre de rotation.; En géométrie dans l'espace, .
Homothétie : facteur d'homothétie et construction
Activités Activité 1 : tracer une figure à l'aide de Scratch Activité 2 : figure à plusieurs motifs Objectif : utiliser un bloc utilisateur Pour créer un bloc, il suffit de cliquer sur mes blocs puis créer un bloc et donner un nom à votre bloc.Méthode 1 : Utiliser les longueurs des côtés.L'homothétie de centre O et de rapport −1 est la symétrie de centre O. Un angle de rotation. Ce chapitre contiendra cinq parties : Comprendre ce qu'est une homothétie. Que signifie agrandir, réduire une figure ? La notion d'agrandissement-réduction n’est pas véritablement une notion mathématique. Calculs de longueur. Le périmètre, généralement noté P, est la mesure du contour d’une figure. Sans changer l’écartement . L' image de toute figure par une telle application est une figure semblable, c'est-à-dire intuitivement « de même forme ».La géométrie est une discipline aux nombreuses facettes et il est possible d’imaginer des fonctions dans tous les espaces géométriques existants, comme des espaces en dimension 4 ou supérieure ou encore des espaces non euclidiens dans lesquels les distances sont déformées. 🤔 Définition .L'homothétie conserve l'alignement et les mesures d'angles. Transformer une figure par rotation, c'est la faire tourner autour d'un point. Des figures, leurs sommets et leurs côtés.
Les transformations
Elle peut être de rapport positif ou négatif et il existe une méthode bien précise pour construire l'image d'un .frHomothéties : exercices de maths en 3ème corrigés en PDF. La première méthode pour trouver le rapport d’une homothétie consiste à utiliser les longueurs des côtés de la .L'homothétie est une transformation de plan qui transforme les dimensions des figures de départ.Reconnaître des figures géométriques. Elle a été créée pour éviter de parler d'homothétie . Pour le calculer, .Cette introduction un peu longue visait à situer l’approche de la géométrie que nous avons commencé à élaborer à l’IUFM Nord Pas-de-Calais dans une perspective plus large de réflexion sur ce que pourrait être une progression de l’enseignement de la géométrie plane au long de la scolarité obligatoire. Il s'agit d'une réduction lorsque 0 < k < 1. Une homothétie conserve l'alignement, le parallélisme et les angles.
Fonctions géométriques
Aucun résultat. La figure et son image par une homothétie ne sont superposables que si k = 1 ou k = -1.

Symétrie axiale : Définition 1 : Transformer une figure par une symétrie axiale, c’est créer l’image de cette figure par pliage le long de l’axe. Placer le centre d'une homothétie.

hénagone ou monogone (figure impossible en géométrie euclidienne) 2 cotés. Construction d'un bloc nommé carré : Nous allons créer. Elle se caractérise par son .






