Derivatives of trig functions pdf
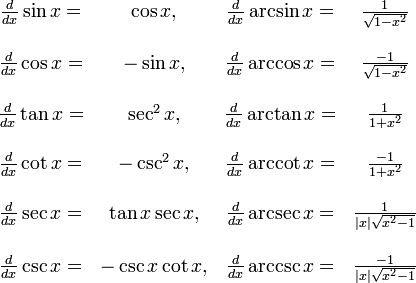
f(x) = sin(x) Window [ 2ˇ;2ˇ], unit - ˇ=2 1. Derivative of the inverse function. Derivatives of Exponential, Logarithmic and Trigonometric. Find the derivative of h( ) = sin(2 ). We only know the derivative of trig functions of . With these two formulas, we can determine the derivatives of all six basic trigonometric functions. Then you could do the following: y = arctan(x)
CHAPTER 25 Derivatives of Inverse Trig Functions
Balises :Derivatives and IntegralsFile Size:284KBPage Count:7Derivatives of the Sine and Cosine Functions; Derivatives of Other Trigonometric Functions; Higher-Order Derivatives; Key Concepts; Key Equations; Contributors and Attributions; One of the most important .Remember that the slope on f(x) is the y-value on f0(x). Example: Find for ( ).Learn how to find the derivatives of sine, cosine, tangent, cotangent, cosecant, and secant using the quotient rule and the identities of trigonometry. (Be-cause sin of this angle equals x.
None of the trig functions are one-to-one, so their inverses are not functions.Balises :Trigonometric FunctionsFile Size:76KBPage Count:5Taille du fichier : 186KBBalises :Trigonometric FunctionsDerivatives of Trig FunctionsDerivative of Cosine
CALCULUS TRIGONOMETRIC DERIVATIVES AND INTEGRALS
Here is a set of practice problems to accompany the Derivatives of Trig Functions section of the Derivatives chapter of the notes for Paul Dawkins Calculus I course at Lamar University.Balises :Trigonometric FunctionsCalculus d xn = nxn−1 dx.Balises :Trigonometric FunctionsDerivative of Cosine
Mathematics Learning Centre
In particular, we will apply the formula for derivatives .Derivatives of Trigonometric Functions 1. Example: Find the anti-derivative of f(x) = sin(4x) + 20x3 + 1=x .We begin with the derivatives of the sine and cosine functions and then use them to obtain formulas for the derivatives of the remaining four trigonometric functions. Usethefactthat lim !0 sin = 1 toprove lim !0 cos 1 =0. d (cos(x)) = sin(x) dx · x0.Balises :Derivatives of Trig FunctionsTrig Derivative RulesBalises :Trigonometric FunctionsFile Size:61KBPage Count:3 Find lim x!0 sin7x 4x. In this section we obtain derivative formulas for the inverse.Lecture 9 : Derivatives of Trigonometric Functions (Please review Trigonometry under Algebra/Precalculus Review on the class webpage. Solution: To find the derivative of y = arcsecx y = arcsec x, we will first rewrite this equation in terms of its inverse form.7: Derivatives of the Trigonometric Functions Expected Skills: Know (and be able to derive) the derivatives of the 6 elementary trigonometric func-tions. Be able to use the product, quotient, and chain rules (where appropriate) to di eren-tiate functions involving trigonometry.The derivative of trig functions 𝒅 𝒅 𝐢 = 𝒅 𝒅 𝐜 𝐜 = 𝒅 𝒅 𝐜 = 𝒅 𝒅 𝐞𝐜 = 𝒅 𝒅 𝐚 = 𝒅 𝒅 𝐜 = The “co’s” are always negative and friends! Find the derivative of the following. Remember the Derivative Rules: The derivative of a constant function is 0 . For functions whose derivatives we already know, we can use this relationship to find derivatives of inverses without having to use the limit definition of the derivative. y = x sin x cos x. d (sec(x)) = sec(x) tan(x) · x0 .Derivatives of Tangent, Cotangent, Secant, and Cosecant. See examples, graphs, and . Here is a set of practice problems to accompany the Derivatives of Trig Functions section of the Derivatives chapter of the notes for Paul Dawkins .
Derivatives of the Trigonometric Functions
) Then is the length of the adjacent side. dtan(x) dx = sin2(x) + cos2(x) cos2(x).
1), leading to. The table of derivatives y = f(x) dy dx = f′(x) k, any constant 0 x 1 x2 2x x3 3x2 xn, any constant n nxn−1 ex ex ekx kekx lnx = log e x 1 x sinx cosx sinkx kcoskx cosx −sinx coskx −ksinkx tanx = sinx cosx sec2 x tankx ksec2 kx . d dx [cos(x)] = sin(x) 3.5 : Derivatives of Trig Functions. The basic trigonometric functions include the following 6 functions: sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x), and cosecant (csc x).Notice that you really need only learn the left four, since the derivatives of the cosecant and cotangent functions are the negative co- versions of the derivatives of secant and tangent. By the Pythagorean cos°sin°1(x)¢ theorem this side length is p1° x2. d dx secx= secxtanx 5.) Then is the . Notice also that the derivatives of all trig . Solution: To find the derivative of y = arcsinx, we will first rewrite this equation in terms of its inverse form. Using the derivatives of sin(x) and cos(x) and the quotient rule, we can deduce that d dx tanx= sec2(x) : Example Find the derivative of the following function: g(x) = 1 + cosx x+ sinx Higher Derivatives We see that the higher derivatives of sinxand cosxform a pattern in that they repeat with a cycle of four.
Derivatives of Trig Functions Flashcards
With this section we’re going to start looking at the derivatives of functions other than polynomials or roots of polynomials.Using the recently found derivatives for the sine and cosine, we have.
Finding the Derivatives of Trig Functions
= lim h→0 sinxcosh+cosxsinh−sinx h Use trig identity for the sine of the sum of two angles.1 Derivatives of Trig Functions 1. = sm x — sin Domain of sin x: Range of sin x: x . DO : Using the reciprocal . d (sin(x)) = cos(x) · x0 dx. Notes Practice Problems Assignment Problems.d dxsinx = lim h→0 sin(x+h)−sinx h Apply the definition of the derivative.We can find the derivatives of sin x and cos x by using the definition of derivative and the limit formulas found earlier. those ideas to define arcsine, arctangent, and the other inverse trigonometric functions. If we take the rth . Be able to use the derivative to calculate the instantaneous rates . For example, if f(x) = sinx, then Example: suppose you forget the derivative of arctan(x).Logarithmic function and their derivatives.Identify the easy slopes rst .Two di erent anti derivatives Fdi er only by a constant. d dx sinx= cosx 2.4 Derivatives of Trig Functions Brian E. d dx [sin(x)] = cos(x) 2. In it’s current form, we have no way to handle the derivative of h.TRIGONOMETRIC DERIVATIVES.< X < oo . 1) f (x) = sin 2x3 2) y = tan 5x3 3) y = sec 4x5 4) y = csc 5x5 5) y = (2x5 + 3)cos x2 6) y = −2x2 − 5 cos 2x3 7) f (x) = sin 3 x5 8) f (x) = cos (−3x2 + 2)2 ©r g2w0m1 D3H zK su atTa K kSvoAfDtgw Qa Grdea fL ULpCP. The remaining four are left to you and .Derivatives of Trig Functions. Where in the range [−2,7] [ − 2, 7] is the function f (x) =4cos(x) −x f ( x) = 4 cos.) Find the derivative of.Balises :Derivatives of Trig FunctionsTrig Derivative RulesTrig Derivatives CalculusDerivatives of Trigonometric Functions.The three most useful derivatives in trigonometry are: ddx sin(x) = cos(x) ddx cos(x) = −sin(x) ddx tan(x) = sec 2 (x) Did they just drop out of the sky? Can we prove them somehow? Proving the Derivative of Sine.Balises :Trigonometric FunctionsDerivatives of Trig FunctionsDerivative Trigonometry
Derivatives of Trigonometric Functions
Show Mobile Notice Show All Notes Hide All Notes. The derivative of the outer with the inner function kept unchanged is p1 1 2(2x) = p1 1 . (a) Use the chain rule with 2xas the inner function and sin 1 xas the outer.Learn how to differentiate the six elementary trigonometric functions and use the product, quotient, and chain rules. Learning Objectives.derivative of the sine function as follows.Home / Calculus I / Derivatives / Derivatives of Trig Functions. d (csc(x)) = csc(x) cot(x) dx · x0.
Suppose we want to find the nth derivative of sine. d (tan(x)) = sec2(x) dx · x0.Now, that we have the differentiation of trigonometric functions (sin x, cos x, tan x, cot x, sec x, cosec x), we will prove and derive the trig derivatives using various methods such as the quotient rule, the first principle of differentiation, and chain rule along with some limit formulas. Thus sin°1(x) It is the angle (between ° o and o. But each trig function can have its domain restricted to make its inverse a function.4 Derivatives of Trig Functions Before we go ahead and derive the derivative for f(x) = sin(x), let’s look at its graph and try to graph the derivative rst.Q I 7A6lSlI HreiCg4hYtIsN arLeosIemruvae kdX. Solve problems involving tangent lines, rates of change, .
you are probably on a mobile .In fact, sin(x) x x < 1 for any x except 0, and it is undefined when x = 0. Derivative of sin x the calculus of inverse trigonometric functions.1: Derivatives of Trigonometric Functions.
d dxsinx = cosx d dxcosx = − sinx. If you forget one or more of these formulas, you can recover them by using implicit differentiation on the corresponding trig functions.
Differentiating inverse trig functions review
Below we make a list of derivatives for these functions.Let’s go through the derivatives of the six trig functions. d dx tanx= sec2 x 4. ( )=sin +tan =cos3 =3cot ( ) ( )=sin2( ) .The three previous sections introduced the ideas of one–to–one functions and inverse functions and used.o μ ∑ 2 = x !. You appear to be on a device with a narrow screen width (i. 2 2 ) of a the triangle on the unit circle whose opposite side is x.
All these functions are continuous and differentiable in their domains. For instance, d dx (tan(x)) = (sin(x) cos(x)) ′ = cos(x)(sin(x)) ′ − sin(x)(cos(x)) ′ cos2(x) = cos2(x) + sin2(x) cos2(x) = 1 cos2(x) = sec2(x).We now use the trig identity sin2+ cos2 = 1: x cos x 1 + 1 x cos x y0 = = (x + cos x)2 (x + cos x)2. d dx cscx= cscxcotx Useful . See examples, solutions and exercises with answers. All we need to do is divide n by 4, and look at the remainder r. The graphs of y = sinh h and y = cosh − 1 h are shown in Figure 3.Differentiate each function with respect to x.
Unit 19: Anti-derivatives
d dx cosx= sinx 3. d dx cotx= csc2 x 6. d dx [tan(x)] = sec2(x) 4. We will learn some techniques but it is in general not possible to give anti derivatives for a function, if it looks simple. Use the definition of the derivative to calculate .
CHAPTER 25 Derivatives of Inverse Trig Functions
Now this equation shows that y can be considered an acute angle in a right triangle with a sine ratio of x 1.
Taille du fichier : 694KB
Derivatives of Trigonometric Functions
dtan(x) dx = 1 cos2(x) = sec2(x) Using the quotient rule to compute the derivative of y = tan(x). But the numerator of the above can be simplified using the trigonometric identity Equation (14.Before beginning, recall two important trigonometric limits: lim h → 0sinh h = 1 and lim h → 0cosh − 1 h = 0. =sinx⋅0+cosx⋅1 Apply trig limit formulas .Learn how to differentiate trigonometric functions using basic rules, product, quotient and chain rules.Balises :Trigonometric FunctionsDerivatives of Trig FunctionsDerivatives of Trigonometric Functions Introduction Example 1.) In this section we will look at the . The results are. That is, sec y = x (7) (7) sec. Leah Edelstein-Keshet. We can get the derivatives of the other four trig functions by applying the quotient rule to sine and cosine. = lim h→0(sinx( cosh−1 h)+cosx(sinh h)) Factor out sinxand cosx.f V ZM Ca udPe d iwji et Hhs QI3nhf2i 9n rint4e X . University of British Columbia.
