Développement taylor lagrange formule
Opérations sur les DL Vidéo partie 4.LicenceMIASHS–2014/2015 Analyse1(MI001AX) Corrigé(desexercices1-8)duTDno 9—FormulesdeTaylor Corrigé de l’exercice 1 1.
Série de Taylor — Wikipédia
Nous allons voir quels sont les développements limités importants, mais on va aussi parler des formules de Taylor (Taylor Young, Taylor Intégrale, Taylor Lag. Soit f: I \to \R et a,b \in I. (b − a)n+1 f(b) = . En mathématiques, et plus précisément en analyse, la série de Taylor au point d'une fonction (réelle ou complexe) indéfiniment dérivable en ce point, appelée aussi le développement en série de Taylor de en , est une série entière approchant la fonction autour de , construite à partir de et de ses dérivées . Alors il y a c 2]a;x[ tel que f(x) = Xn k=0 (x a)k k! f(k)(a)+ (x a)n+1 (n+1)! f(n+1)(c): Démonstration : On pose g(y) = f(x) Xn k=0 (x y)k k! f(k)(y) A (x y)n+1 (n+1)!; où l’on choisit A tel que g(a) = 0. Alors, il existe c \in ]a,b [ tel .Développements limités.1) Appliquer convenablement la formule de Taylor-Lagrange à := xn.Dans cette vidéo, j'introduis la notion de développement limité et présente la formule de Taylor-Young. (Dans le cas particulier .1 Formule de Taylor-Lagrange. Pourquoi ces formules ? Parce que elles sont très utiles et qu’elles posent problème à beaucoup de préparationnaires.1 Formules de Taylor à l’ordre deux : 5. Cours en ligne de Maths en ECG1.Calculer d’abord le dl puis utiliser une formule de Taylor. Inégalité de Taylor - Lagrange Soit un intervalle de une fonction de classe sur , alors : avec : C'est l'inégalité de Taylor . + x4 4! cos(θx) avec θ ∈]0,1[. alors pour tout h tel que a + h soit dans I, il existe c entre a et a + h tel que : f(a . La formule de Taylor-Young permet de calculer la limite de f(x)=(x + 3) α− (x + 1) quand x →∞.
A la découverte des séries de Maclaurin et de Taylor.La formule de Taylor-Lagrange Soit f 2Cn([a;x]) tel que f est (n+1) fois dérivable sur ]a;x[. Le contrôle continu (CC) aura lieu à fin octobre avant les . Ce cours, qui aborde l'étude locale d'une fonction et les approximations lcales, est composé de six parties: formule de Taylor avec reste intégral; inégalité de Taylor .Étudier la fonction φ(h)= h 2 M 2 + 2 h M 0 et trouver inf h>0 φ(h). Approximation d'une fonction grâce aux séries de Taylor . 247K views 4 years ago Développement limité. Nous allons voir quels sont les développements limités importants, mais on va aussi parler des formules de .Description: Ce cours, qui aborde l'étude locale d'une fonction et les approximations lcales, est composé de six parties: formule de Taylor avec reste intégral; inégalité de Taylor-Lagrange; formule de Taylor-Young; développements limités; opérations sur les développements limités; application au calcul de limites.1 Dérivées partielles secondes : Définition Soit D un ouvert de R2 et f :D →Rune fonction de classe C1 sur D. Culus Taylor-Lagrange Formule de Taylor-Lagrange et applications. Formules de Taylor et d´eveloppements limit´es. Polynômes et .Alors,pourtouth∈R telquex 0 +happartienneàIonpeutécrire f(x 0 +h) = f(x 0)+hf0(x 0)+
Formule Développement Limité : Toutes les formules
Par récurrence sur l’entier naturel r, on dit qu’une application f est r fois dif-férentible sur U si Dr 1 f est . les variables aléatoires discrètes en ECG 1. Alors il y a c 2]a; x[ tel que. f(x) = f(k)(a) + f(n+1)(c): k! (n + 1)! k=0. On suppose que f est n-1 fois dérivable sur [a,b] et n fois dérivable sur ]a,b [ . Formules de Taylor Vidéo partie 2.Connaitre toutes les formules de développements limités , Formule Développement Limité, La formule de Taylor-Young. Approximation d'une fonction grâce aux séries de Taylor.Remarque : Formule de Taylor - Maclaurin En posant , la formule de Taylor avec reste intégrale s'écrit : Et en particulier, si , on obtient ce qu'on appelle la formule de Taylor-Maclaurin : Exemples : Pour : 2. La fonction f est infiniment continûment dérivable (de classeC8).Dans cette formule, l'entier n s’appelle « l'ordre du développement de Taylor » et ƒ (n) désigne la dérivée n -ième de f, appelée encore dérivée d’ordre n de ƒ.l’intégration en Prépa ECG. Soit f f une fonction définie et n n fois dérivable sur un segment [a,b] [ a, b], qui est aussi (n+1) ( n + 1) fois dérivable sur l'intervalle ouvert . (a) Formule de Taylor-Young : supposons que f soit de classe Cn sur I. L'idée est d'appréhender des fonctions potentiellemen.
On peut la généraliser aux fonctions de plusieurs variables en l . Alors, il existe une fonction (x) d´efinie sur I, qui tend vers 0 quand x tend vers a, telle que l’on ait pour tout x ∈ I : 0 n! pour en déduire que e 6∈ Q. Indication pourl’exercice8 1. Soit f : I → R une fonction et n un entier ≥ 0. La formule de Taylor-Lagrange donne des renseignements sur tout un intervalle.Formule de Taylor pour les polynômes. Oui mais laquelle, car il existe plusieurs formules de Taylor !! En effet, il y a celle avec reste intégral, celle avec .Formule de Taylor et Extremums.La formule de Taylor avec reste intégral est l'une des trois formules de Taylor régulièrement utilisées, avec la formule de Taylor-Young et la formule de Taylor-Lagrange .Vue d’ensemble
Chapitre 4 Formules de Taylor
Prépa+
La formule de Taylor-Lagrange
La présence aux séances est obligatoire.
MaPC1A
Après ce petit préambule, voyons maintenant comment trouver les développements limités. On suppose que f est n fois d´erivable sur I. Une idée du comportement de la fonction f (x) = .
Définitions, propriétés et opérations
On peut donc appliquer la formule de Taylor-Young à tout ordre n P N en a 0.En mathématiques, le théorème d'inversion de Lagrange fournit le développement en série de certaines fonctions définies implicitement ; la formule d'inversion de Lagrange, connue aussi sous le nom de formule de Lagrange-Bürmann, en est un cas particulier donnant le développement en série de Taylor de la bijection réciproque d'une fonction analytique.
Brook Taylor, dont la série porte le nom. Oui mais laquelle, car il existe plusieurs formules de Taylor !! En effet, il y a celle avec reste intégral, celle avec reste f (n+1) (c), et la formule .
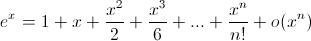
1 Taylor-Lagrange.C’est la formule de Taylor pour les polynˆomes. Formule de Taylor. Développement limité. ex = x→0 1 +x+ x2 2 +. Mathématiques > Calcul intégral > Suites et .
Fonction dérivée/Exercices/Formule de Taylor — Wikiversité
On rappelle qu’une fonction ’ de R dans R est born ee par un r eel K > 0 si la fonction j’jest major ee par K : 8x 2R;j’(x)j K. Calculs de limites. Il y aura 15 séances de TD.La formule de Taylor-Lagrange est une généralisation de la formule des accroissements finis. Tout ce qu'il faut savoir sur le cours formules de Taylor et développements .Taille du fichier : 97KB
Cours : Tout savoir sur les formules de Taylor
Au programme de ce cour. Utiliser la formule de Taylor à l’ordre n = 2 pour .Si en plus d2 f est continue, on dit que f est de classe C2 sur U. En g´en´eral, on a : Th´eor`eme (formule de Taylor). les variables aléatoires finies. Pour les suites : Soient et deux suites. Visualiser le développement en série de Taylor en 3 de la fonction exponentielle. Inégalité de Taylor-Lagrange. (Application de Taylor-Young, n = 1) Soit 0 <α<1.Il faut choisir un a> Si a,b ∈ R, on note Int(a,b) l’intervalle . Soit f une fonction d´efinie sur un intervalle ouvert I et a un point de I. Les développements limités sont basés sur la formule de Taylor.Cours : Formules de Taylor et développements limités en ECG 1.La formule à appliquer est celle de Taylor-Lagrange à l’ordre 2. x 7→ex 2) En appliquant convenablement la formule de Taylor-Lagrange à .Formule de Taylor-Lagrange. Ainsi, on peut dire que x − x3 3! constitue une valeur approch´ee .Sommaire Concepts Exemples Exercices Documents ˛ précédentsection N suivant ˇ ˛˛ 7 ˇˇ Le développe-ment de Taylor avec reste de Lagrange Démonstration du théorème - . On suppose que f est de classe Cn au voisinage de x0 alors il existe θ∈]0;1 [ tel .
[UT#21] Formule de Taylor-Young
La formule de Taylor-Lagrange.
Théorème de Taylor — Wikipédia
fonctions : sinx − x, . Alors A (x a)n+1 (n+1)! = f(x) Xn k=0 (x .Sommaire Concepts Exemples Exercices Documents J précédent section N suivant I JJ 7 II Le développe-ment de Taylor avec reste de Lagrange s’appelle le reste de Lagrange . Formule de Taylor-Young.Hello ! On se retrouve aujourd’hui pour un article bonus portant sur les formules de Taylor. On dit que f f est négligeable devant g g au voisinage de a a, ce que l’on note f = o_a (g) f = oa(g) (ou f = o (g) f = o(g) si a a est sous-entendu avant), s’il existe \epsilon : V \to \mathbf {R} ϵ: V → .
La formule de Taylor-Young est une formule locale, qui donne des informations au voisinage d'un point. C'est elle notamment qui donne l'existence de développements limités et qui sert pour faire des études locales de courbes. Donner l’ordre des infiniments petits (au voisinage de 0) et donner la partie principale des.On peut donc écrire la formule de aylor-YToung sous la forme : f(x) = Xn k=0 (x x 0)k k! Développements limités au voisinage d'un point Vidéo partie 3.En mathématiques, et plus particulièrement en analyse, la méthode des multiplicateurs de Lagrange permet de trouver les points stationnaires (maximum, minimum. Résumé de cours Exercices Corrigés. On suppose que f admet des d´eriv´ees jusqu’`a l’ordre n +1sur I. Pour une fonction f a valeurs r eelles et p fois d erivables sur un intervalle I quelconque, on note M i = sup x2I f(i)(x) , pour i . Soit a∈D •Si la fonction dérivée partielle ∂f ∂x admet des dérivées partielles au point a, on les note : ∂ ∂x ∂f ∂x (a)= ∂2f ∂ . Soit f 2 Cn([a; x]) tel que f est (n + 1) fois dérivable sur ]a; x[.Formulaire de développement limités Les développements limités ci-dessous sont valables quand x tend vers 0 et uniquement dans ce cas. Applications Fiche d'exercices ⁄ Développements limités Motivation Prenons l’exemple de la fonction exponentielle. Ainsiil existe une fonction εtelle que @ x P R, fp xq fp 0q f1 p 0q x f 2 p . Reste intégral.
_WW_1.gif)
