Direct strain formula
They are also mentioned as directly proportional or inversely proportional. The straining of any elastic material will give rise to a change in lateral dimensions and, hence, to lateral strains in all directions at right angles . Aȳ = Moment of area of the area above XY line about Neutral axis. A force of 40 Newtons was applied at the end of a wire of length 4 meters and diameter 2.Strain Energy Formula.Stiffness of the spring = direct stress σ /direct strain ε The modulus of elasticity E can be derived from Hooke’s law. Alternatively allowing z to be a variable:.By substituting our figures into the main formula, Strain = 0. There are two ways of deriving the .75, and it takes 0.
Direct Strain
It is generally denoted by K.
Types of Strain
3: General Concepts of Stress and Strain
( 1 + ν)) General Formula for Torsion .
Fatigue Crack Propagation Estimation Based on Direct Strain
Shear strength formula Various methods can be implemented to determine the shear strength of soil material under various conditions.
Normal strain
Average Normal (extensional) Strain: Length change divided by total length: Engineering or nominal (normal) strain: Average normal strain using original (undeformed) total length.In the early (low strain) portion of the curve, many materials obey Hooke’s law to a reasonable approximation, so that stress is proportional to strain with the constant of .
Kinematic equation: The \(x\)-direction normal strain \(\epsilon_x\) is then the gradient of the displacement: \[\epsilon_x = \dfrac{du}{dx} = -yv_{,xx}\] Note that the . Illustrating the case when M is related, very simply to x . When a force acts parallel to the surface of an object, it exerts a shear stress. In the linear limit of low stress values, the general relation between stress and strain is [latex] \text{stress}=\text{(elastic modulus)}\,×\,\text{strain. It’s the ratio of axial deformation to the original length of the member. The shear strain is proportional to the . In this direct variation equation, 7 is the constant of proportionality, which represents the cost per item.Strain is the measure of the deformation produced in a member by the applied Load. Example Problem. In this case of uniform stress, we also have uniform strain, and each element has the same strain. We define the (often just called normal strain. b = Width of the layer where shear stress has to find.Compressive Strain Formula \(Compressive Strain=frac{Decrease in length}{Original length}\) Shear Strain. Linear strain of a deformed body is defined as the ratio of the change in length of the body due to the deformation to its original length in the direction of the force.
Manquant :
direct strain4 Direct Stress
E = direct strain (E) (d) Lateral Strain.
Transverse shear stress: Definition, Formula, Examples
One of the most common problems in mechanics of materials involves transformation of axes.

This is called welding-induced distortion. Displacement Encoding with Stimulated Echoes cardiac image phases a .
Direct and Inverse Proportion
This study's purpose was to develop a direct MRI-based, deep-learning semantic segmentation approach for computing global longitudinal strain (GLS), a known metric for detecting left-ventricular (LV) cardiotoxicity in breast cancer. In the linear portion of the stress-strain diagram, the tress is proportional to strain and is given by.The other direct strains are obtained in a similar way; thus the rates of direct strain are given by (2.1) σ S = F tan A.

Problem 1: An elastic band of length 5 cm is stretched such that its length increases by 2 mm. Moreover, operational loads may vary between individual aircraft, therefore it is crucial to understand the whole process of fatigue crack onset and development in order to determine safe inspection intervals and thereby mitigate risk. Strain Counterstrain is a manual therapy technique, meaning clinicians use only their hands for treatment of muscle and joint pain. Relative change in length of a line element oriented in arbitrary direction n n. For a gradually applied or Static load the . The plastic strain results in permanent deformation of the welded structure after the welding.Strain Energy Direct Shear. In welding, plastic thermal strain develops near the weld region because of heating, melting and cooling of the weldment and the nearby base metals. Shear strain is the ratio of transverse shear displacement to the original length. Underneath are numerical founded on strain formula which might be useful for you.
Direct Stress and Strain
Axial Deformation. According to Hooke’s law, the strain in a . To use this formula, the load must be axial, the bar must have a uniform cross-sectional area, and the stress must not exceed the .academyLearn about 3 different types of loading for engineering components: tension, compression and shear. Bulk Modulus (K): When a body is subjected to stresses of equal intensity in 3 mutually perpendicular directions, then the ratio of this direct stress to the volumetric strain is called Bulk modulus.Regarder la vidéo2:33This mechanics of materials tutorial introduces the concept of normal strain.Just like stress, there are two types of strain that a structure can experience: 1.σT = F⊥ A (26. Qin Xu, Katharine E. Normal Strain and 2. Calculate the stress and the strain on the wire. The labor cost per unit is obtained by multiplying the direct labor hourly rate by the time required to complete one unit of a product. Direct stress and strain • Young's modulus of elasticity • Change in length • Lateral strain • Poisson's ratio • Change in volume • Stresses in thin-walled cylinders. A shaft subject to a torque T having a polar moment of inertia J and a shear Modulus G will have a shear stress q at a radius r and an angular deflection θ over a length L as calculated . For example, if we say, a is proportional to b, then it is represented .The polar coordinate system is a special case with z = 0 z = 0. The components of the displacement vector are {ur,uθ,uz} { u r, u θ, u z }. Among which one of the most common and simplest methods is the direct shear test using shear box apparatus which can be used to determine the shear strength parameters, cohesion (c), and internal angle of . Producing Strain). Fitting these data to the form ϒ = ϒ 0 + Λ \ (\epsilon\), we find ϒ 0 = 19 ± 3 . The ratio of the amount the section has stretched to the original length is called the tensile strain, εT = δl l0 (26.Direct measurement of strain-dependent solid surface stress. Compute the strain.Only when stress is sufficiently low is the deformation it causes in direct proportion to the stress value. Problem: A pin with a circular cross-section of radius R = 5 cm is subjected to a transverse force of F = 5000 N. Strain Energy Beam in bending. Stress is directly proportional to strain whilst the material is . Which implies that Strain = 0.individual direct strains with all direct (diagonal) components of the stress tensor.The Strain Energy of the bar is defined as the work done by the load in altering the length (i. 9 shows the strain curves of the specimen transverse axis center line calculated by the aforementioned three methods and real strain curve (black line), which was obtained by the theoretical calculation formula, when a 20-μ m displacement occurred at the free end of the cantilever beam.In the linear portion of the stress-strain diagram, the tress is proportional to strain and is given by $\sigma = E \varepsilon$ since $\sigma = P / A$ and $\varepsilon = \delta / L$, .In continuum mechanics, lateral strain, also known as transverse strain, is defined as the ratio of the change in diameter of a circular bar of a material to its diameter due to .138) d ε x x d t = ∂ u ∂ x , d ε y y d t = ∂ v ∂ y , d ε z z d t = ∂ w ∂ z In this way we . When x=10, y=70.
Definition, Stress-Strain Curve, Hooke’s Law, SI Units
It is usually denoted by U.The formula for calculating volumetric strain is as follows: ε = ΔV/V.Normal strain Now we consider the resulting deformation. The curve result of the proposed method was the smoothest and . If the pin is supported by two fixed leaves, calculate the average shear stress in the pin.Transverse shear stress formula: The transverse shear stress at any layer of the cross-section (line xy in figure) can be given by, τ = F A¯y I b τ = F A y ¯ I b.It means a direct length-changing stretch (or compression) of an object resulting from a normal stress. The result is expressed as a decimal or a percentage. Strain energy is defined as the energy stored in a body due to deformation. And, for example: When x=2, y=14. For instance, we may know the stresses acting on xy planes, but are really more interested in the stresses acting on planes oriented at, say, 30∘ to the x axis, perhaps because these are close-packed atomic planes on which . Where ΔV is the change in volume of the material or object, and V is the original volume. When the applied force is released, the whole system returns to its original shape. Note that strain is unitless and measures the fractional elongation. The proportionality constant in this relation is called the elastic modulus. For instance, we may know the stresses acting on xy .Torsion /Shear.https://engineers.Strain Solved Examples.The shear stress is defined to be the ratio of the tangential force to the cross sectional area of the surface upon which it acts, σS = Ftan A (26. In this case, body displace transversely from its original position.T he general equation for volumetric strain is given as –. where the quantities are defined in the sketch. The strain energy per unit volume is known as strain energy density and the area under the stress-strain curve towards the point of deformation. Direct Stress produces a change in length in the direction of the Stress.Direct and Inverse Proportion. Discover the formulas used when.
Beams Formulae
εv = δV / V=ε {1- (2/m)} where, ε = Linear strain.
Thermal Strain
1 Introduction.In its simplest terms, Hooke's Law states that the strain experienced by an object is directly proportional to the applied stress and inversely proportional to the object's . The beam is subject to stresses as a . It is commonly defined as. Known: The strain is given by. Style & Eric R.Dividing this equation by tensile strain, we obtain the expression for Young’s modulus: \[Y = \frac{tensile\; stress}{tensile\; strain} = \frac{\frac{F_{\perp}}{A}}{\frac{\Delta L}{L_{0}}} . When a force acts perpendicular (or normal) to the surface of an object, it exerts a normal stress.The proposed usage of direct strain data from the test include such local effects. If l is the original length and dl the change in length occurred due to the deformation, the linear strain e induced is given by e=dl/l.
Manquant :
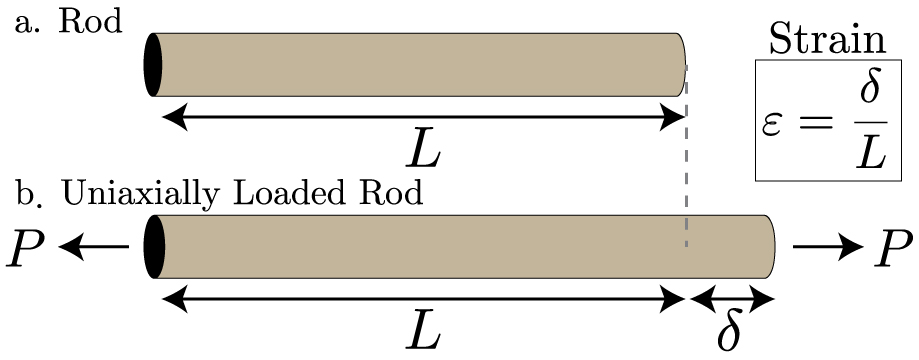
strain) on the object to be 𝜖= 𝛿/𝐿.Manquant :
direct strain K =Direct Stress/Volumetric strain .2) ε T = δ l l 0. When x=3, y=21. It uses passive body positioning . Strain Energy due to tranverse shear stress Consider a beam subject to traverse shear loading as shown.For example, if y represents the total cost of buying x items that cost $7 each, then the direct variation equation would be.1) σ T = F ⊥ A.Auteur : Engineer4Free} [/latex] As we can see from . Hooke’s law explains the relationship between stress and strain.Over the range of measured strains, up to ~25%, we find that the surface stress increases linearly with strain.Calculate the labor cost per unit.Constitutive equation: If the material is in its linear elastic regime, the shear stress is given directly from Hooke’s Law as: \[\tau_{\theta z} = G\gamma_{\theta z} = Gr\dfrac{d .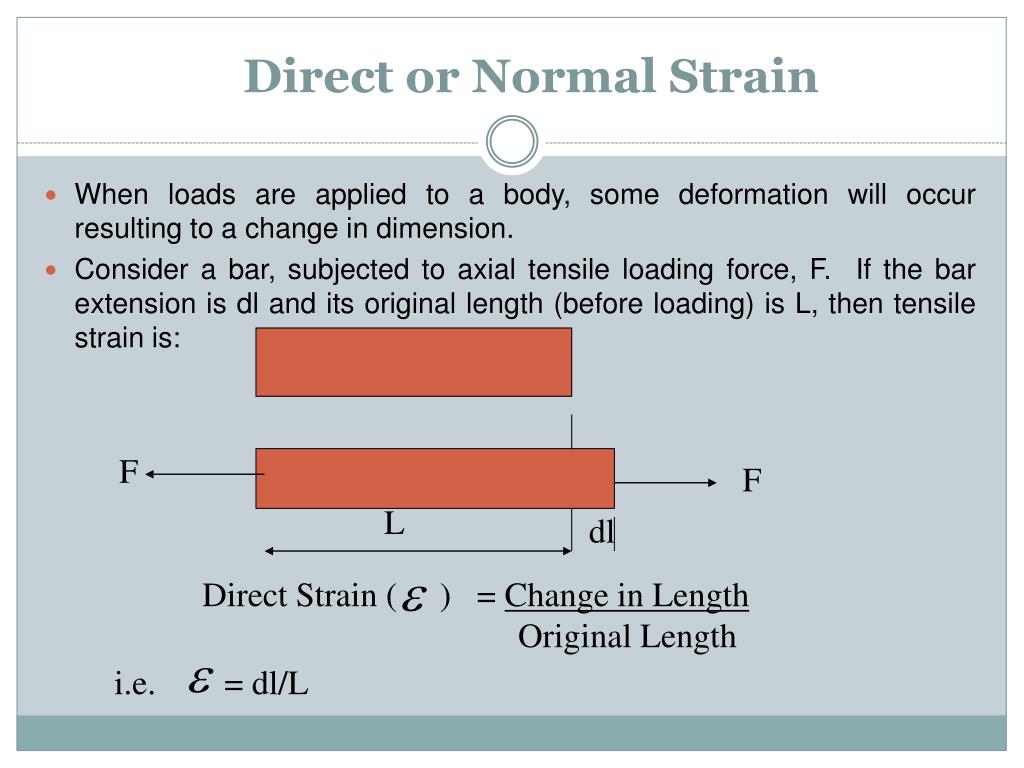
To find the stress, we . A direct and inverse proportion are used to show how the quantities and amount are related to each other.The relation between stress and strain is that they are directly proportional to each other up to an elastic limit. Jensen, Rostislav Boltyanskiy, Raphaël Sarfati, Robert W. Poisson's Ratio = ν = (lateral strain / primary strain ) Shear Modulus G = Shear Stress /Shear Strain G = τ / ε = E / (2 . For example, if a material with an original volume of 100 cubic meters experiences a change in volume of 5 cubic meters due to an .

Let's consider a rod under uniaxial tension.1 hours to manufacture one unit of a product, the direct labor cost per unit equals $1.







