Droite orthogonale à un plan

droites de ce plan. On appelle symétrie orthogonale par rapport à F F l'application qui à tout x x de E E, qui se décompose uniquement en x =y +z x = y + z avec y y dans F F et z z dans F ⊥ F ⊥, associe s(x) = y−z. Application mobile.
Droites et plans dans l'espace
Il n'y a donc plus lieu ici de distinguer orthogonalité et perpendicularité.Propriétés : . Propriétés analytiques. Droite contenue (incluse) dans un plan.Auteur : Mathemax4K subscribers.Méthode pour établir l'équation d'un plan. 2 droites sont perpendiculaires ⇔.Auteur : Galilee acOrthogonalité dans l'espace.Droite strictement parallèle à un plan.
Géométrie Dans l’Espace
Théorème 1: une droite parallèle à une droite d’un plan P est parallèle à ce plan. Comme est une droite du plan P alors D et sont orthogonales.ly/3U9lDwO#maths #terminale #exercicecorrigé Comment savoir si une droite est orthogonale à un plan dans l'espace ?Pour mo.Deux droites sont dites orthogonales lorsque leurs parallèles respectives passant par un même point sont perpendiculaires. Fiche de cours. droite est orthogonale à un . Deux droites qui sont à la fois orthogonales et coplanaires sont dites .Temps de Lecture Estimé: 6 min
Equations de plans
Ainsi pour montrer que D . On note : d ⊥ P. On considère un plan \mathcal {P} de l'espace dont on connaît un vecteur normal \vec {n} et un point \text {M} extérieur au plan \mathcal {P}. Un vecteur \overrightarrow {n} est normal à un plan si et seulement s'il est orthogonal à deux vecteurs non colinéaires de ce plan. Si une droite est orthogonale à deux droites . Exercices de mathématiques pour la classe de Spécialité sur Distance d'un point à une droite ou à un plan dans le chapitre Orthogonalité et distances dans l’espace. Il est inutile de . La droite perpendiculaire à P passant par M coupe le plan P en M ′ appelé projeté orthogonal de sur PLes droites (AE) et (BC) sont orthogonales. Montrer que la droite \text { (AC)} est orthogonale au plan \text { (BAD)}. Exemple : Δ est perpendiculaire à 1 et à 2 qui sont incluses . Déterminer les coordonnées du vecteur ÄAB.Ressources de mathématiques.
L'orthogonalité de deux droites, d'un plan et d'une droite
Une droite est orthogonale à un plan lorsqu'elle est orthogonale à toutes les droites incluses dans ce plan. Elle est aussi perpendiculaire à . Définition : Soit F F un sous-espace d'un espace vectoriel euclidien E E . Dans cette vidéo, tu vas apprendre à montrer qu'un droite est . Un vecteur AB non nul, est normal à un plan P signifie que la droite( AB) est perpendiculaire à ce plan Projection orthogonale sur un plan.
Droites et plans de l'espace
Représenter et caractériser les droites du plan Cours
Et donc la droite (%’) est orthogonale à toutes les . Profs en ligne.
Montrer qu'un vecteur est normal à un plan Méthode
Et réciproquement : Si (d) est orthogonale à (P) alors :vecteur normal à un plan.Définition du produit scalaire. Droite sécante à un plan. La droite d d est .5K views 2 years ago Géométrie dans l'espace - Terminale spécialité. L’angle non orienté entre les . Une droite est orthogonale à un plan ⇔. Si un plan (P) est orthogonal à une droite (D) et coupe cette droite en un point M, alors toute droite passant par M et orthogonale à (D) est dans le plan (P). Démontrer que les plans S et S′ sont perpendiculaires. Comment montrer qu'une.Pour montrer qu’une droite (d) est orthogonale à un plan (P), il suffit de montrer qu’un vecteur directeur de (d) est colinéaire à un vecteur normal de (P). Positions relatives de deux droites. Déterminer les coordonnées d ’un point B situé sur la droite orthogonale en A à P. Révisez en Terminale : Cours Représentation paramétrique et équation cartésienne avec Kartable ️ Programmes officiels de l'Éducation nationale. Cette vidéo se sert de l’outil « Revoir la construction » de Cabri 3D pour . Dans un repère orthonormal, pour déterminer une équation cartésienne du plan (ax + by + cz + d = 0) passant par les trois points non-alignés A, B et C, une méthode consiste à : Déterminer un vecteur orthogonal aux vecteurs et obtenir ainsi un vecteur normal au plan (ABC) et les coefficients .Cela permet de : prouver l’orthogonalité de vecteurs. Propriété : Soit $(D)$ une droite de vecteur directeur $\overrightarrow{d}$ et $\mathcal{P}$ un plan dirigé par un couple de vecteur $(\overrightarrow{u}, \overrightarrow{v})$ non colinéaires et de vecteur normale $\overrightarrow{n}$.
Orthogonalité, projection orthogonale
On considère un plan trois points A, B et C non alignés tels que :
REPRÉSENTATIONS PARAMÉTRIQUES ET ÉQUATIONS CARTÉSIENNES
Dans l’espace, une base ( i; j; k) est orthonormée lorsque les vecteurs de la base ont tous une norme égale à 1 et sont orthogonaux deux à deux. De toute façon, pour montrer que deux droites sont orthogonales ou .Ainsi, (%’) est orthogonale à deux droites sécantes du plan (&BA) : (&B) et ‘. (δ’) (D) (d) ( δ) (∆) y’. Déterminer une équation du plan P orthogonal en A à la droite (AB . Pour que deux plans (P) et (Q) soient orthogonaux, il suffit qu’un vecteur ~v de (Q) soit orthogonal à un couple de vecteurs directeurs (u~1,u~2)de (P).Dans un repère orthonormé, les plans S et S′ ont pour équations respectives : 2/+40+41−3=0 et 2/−50+41−1=0. C’est aussi un livre d’histoire. A l’aide du produit scalaire, nous pouvons démontrer la propriété suivante : Propriété : Si une droite est orthogonale à un plan, elle est orthogonale à toute droite de ce plan. Une droite d est orthogonale à un plan P si elle est orthogonale à au moins deux droites sécantes de ce plan: Si d1 P, d2 P, d1 etd2 sécante, d3 | d1 et d3 | d2 . On donnera la valeur exacte.
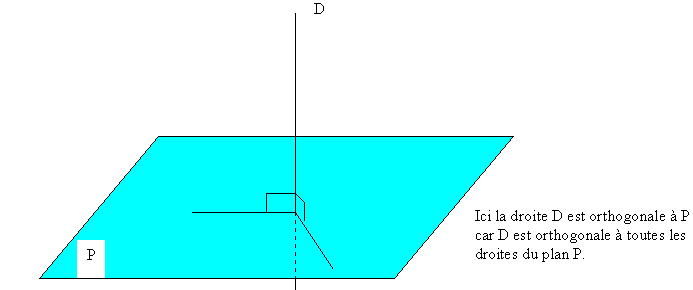
La droite D est orthogonale au plan P.comRecommandé pour vous en fonction de ce qui est populaire • Avis
DROITES ET PLANS DE L'ESPACE
Entre grottes ornées, bourgs de caractère et châteaux forts, on y . Les droites (EF) et (FB) sont perpendiculaires à la (FG) mais elles ne sont pas parallèles ! Orthogonalité d’une droite .frTS - Exercices corrigés - Géométrie dans l'espace - mathsannales2maths.droite orthogonale à un plan de l’espace. Caractérisation d’un plan par un point et un vecteur non nul. Revenir au choix du niveau. Pour un plan défini par ax + by +cz +d = 0, les . cette droite n’est pas parallèle à toutes les droites du plan P. projeté orthogonal d’un point sur un plan.
Manipulation des vecteurs, des droites et des plans de l’espace
3,4/5(20)
ORTHOGONALITÉ DANS L'ESPACE

Une droite est perpendiculaire à un plan lorsqu'elle est orthogonale à toutes les droites de ce plan. $(D)$ est orthogonale à $\mathcal{P}$ si et seulement si :
Distance d'un point à une droite ou à un plan
La droite D' est parallèle à D.Définition 4 : Un plan (P) est orthogonal à un plan (Q) si, et seulement si, il existe une droite d du plan (Q) orthogonale au plan (P).Une représentation paramétrique du plan passant par A(xA yA zA) et de vecteur directeur →u(a b c), →v(a ′ b ′ c ′) est : Pour retenir ce résultat: Un plan n'a pas qu'une seule représentation paramétrique: Pour savoir si un point A appartient à un plan : Pour savoir si une droite est parallèle à un plan : Pour savoir si une .Le concept de projeté orthogonal, ou de projection orthogonale est assez vaste en maths donc pour faire simple, on va garder ce concept à la géométrie dans le plan et dans l'espace.2 Orthogonalité d'une droite et d'un plan DEFINITION: Une droite D est orthogonale à un plan P si elle est orthogonale à toutes les droites de ce plan. Ca peut paraître compliqué mais en fait c’est simple .Orthogonalité et distances dans l’espace | Lelivrescolaire. Théorème 2: un angle droit dans l’espace se projette sur un plan selon un angle droit si et seulement si un de ses côtés est .
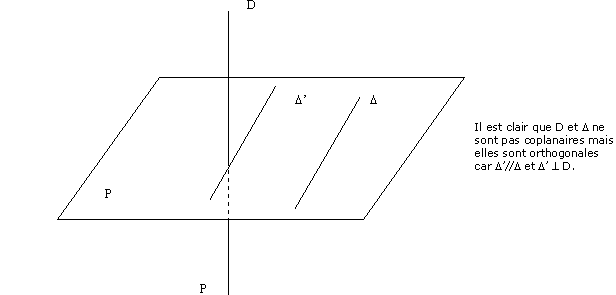
L'orthogonalité d'une droite par rapport à un plan se définit à partir de celle des droites entre elles.Une droite est orthogonale à un plan si et seulement si elle est orthogonale à deux droites de ce plan.
Exemples et exercices
On appelle bicoin un tétraèdre dont les quatre faces sont des triangles rectangles. Si D et D’ sont paralleles, alors tout plan orthogonal à l’une est orthogonal à l’autre. Remarque : Pour tout vecteur , il existe un point tel que ⃗⃗⃗⃗⃗⃗ = ⃗ .II) Orthogonalité d’une droite et d’un plan . Comme dans le plan, on définit les . On considère des points A, B et C tels que →u = → AB et →v = → AC.
Produit scalaire et plans dans l’espace
( ; ; ) alors on appelle l’abscisse, l’ordonnée et la cote du point .Montrer qu'une DROITE est ORTHOGONALE à un PLAN dans l'Espace - Exercice Corrigé - Terminale - YouTube.
Orthogonalité et distances dans l’espace
Orthogonalité et distances dans l'espace
3K views 8 years ago Géométrie espace terminale S.Projection orthogonale d'un point sur un plan ou sur une droite. PROPRIETES: Soit un point A fixé: à un plan donné est orthogonale une unique droite en ce point et à une droite donnée est orthogonal un seul plan en ce point. Deux droites orthogonales à une même troisième droite ne sont pas nécessairement parallèles.(AC) est orthogonale à la droite d. Soient →u et →v deux vecteurs de l’espace.2K subscribers. (D) Théorème 5: pour qu’une droite soit perpendiculaire à un . Donc (%’) est orthogonale au plan (&BA). Dans la vallée de la Dordogne, la pierre blonde est plus qu’un décor.Une droite ( d) est orthogonale à un plan P si et seulement si elle est orthogonale à deux droites sécantes du plan P .
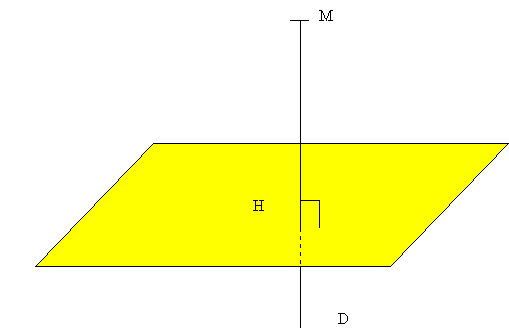
Théorème 4: lorsqu’une droite est perpendiculaire à un plan elle est orthogonale à toutes les.Une droite orthogonale à un plan coupe nécessairement ce plan en un point. 894 subscribers.Pour une droite du plan, il existe une infinité de vecteurs directeurs, et tous ces vecteurs sont colinéaires. Soit $E$ un espace euclidien de dimension $n$.On répondra sous la forme d'un triplet (x; y; z) (x; y; z) Calculer la distance du point A A au plan \mathcal {P} P . Une droite et un plan de l’espace sont parallèles si et seulement si le produit scalaire des vecteurs directeurs de la droite et des . Il permet enfin de .Orthogonal, c’est plus large : dans l’espace, deux droites sont orthogonales si les projetés orthogonaux de ces droites sur un plan sont perpendiculaires, c’est-à-dire que les projetés des droites se coupent à angle droit.Ainsi, (A B) (AB) (A B) est orthogonale à deux droits sécantes du plan (A K C) (AKC) (A K C) donc elle est orthogonale à toute droite du plan (A K C) (AKC) (A K C), en . PROPRIÉTÉ 3: Si . Le plan médiateur d’un segment [AB] [AB] est le plan passant par le milieu I I de [AB] [AB] et orthogonal à la droite (AB) (AB). La droite ( d) est contenue dans le plan P .Une droite est perpendiculaire à un plan si elle est orthogonale à toutes les droites de ce plan, ou bien si elle est orthogonale à seulement deux droites sécantes de ce plan.


La définition précédente parle de .1 Rappeler la définition 2 Déterminer deux vecteurs non colinéaires du plan 3 Calculer les produits scalaires 4 Conclure.Si une droite est orthogonale à un plan, alors elle est orthogonale à toutes les droites du plan. Le projeté orthogonal de \text {M} sur \mathcal {P} est l'intersection du plan et de la droite de vecteur directeur \vec . On ne dit donc jamais « le vecteur directeur » mais « un vecteur . Deux vecteurs non nuls sont orthogonaux lorsque . Exercice 11 Soit les points A(1;2;-1) et B(3;5;2). Déterminer les coordonnées d ’un vecteur Ån orthogonal à ce plan. s ( x) = y − z.













