Est-ce que le rayon spectral est inférieur à la norme d'opérateur

Par r´ecurrence sur m ∈ N, on . L'addition et le produit de Cauchy de deux séries entières munissent $\mathcal A$ d'une structure d'anneau. (a) Montrer que est bien défini pour chaque x.je suis finalement, avec votre aide et celle du polycopié, parvenu à répondre aux questions posées! Les réponses reprennent de nombreux points fondamentaux du cours, combinés à quelques astuces.Rayon spectral d’une matrice. Définition 4.Une norme d'opérateur c'est une norme sous-multiplicative : ||AB|| ≤||A|| ×||B|| | | A B | | ≤ | | A | | × | | B | |. La norme euclidienne. Par conséquent, s(T) = [0, 1].Passons à la limite quand k tend vers l’infini. On appelle rayon spectral de A la quantité ⇢pAq :“ max PSpCpAq | | P r0, `8r. Stigmatisme du dioptre plan.Analyse spectrale.Tracer ρ(Br) ρ ( B r) (le rayon spectral de la matrice d'itération) pour r ∈ [0, 1] r ∈ [ 0, 1] dans chaque méthode.Salut, dans une correction d'épreuves il est écrit que, puisque la matrice M a un rayon spectral strictement inférieur à 1, M^n tends vers la . Index du forum ‹ Entraide Mathématique ‹ Supérieur; Rayon spectral strictement inférieur à . a)i) L'indication permet de se ramener à une dimension . En effet, si le polynôme caractéristique d'une matrice est scindé (c'est-à-dire décomposable en produit de .
Calculer l'angle d'acceptance θ0.Exercices corrigés - Espaces vectoriels normés. Vu que la lumière se réfracte lorsqu’elle se déplace d’un milieu avec un indice de réfraction moins grand à un milieu . Que signifie le terme lumière monochromatique en optique. Extrait gratuit de document, le document original comporte 5 pages. Tracer le graphe de la fonction f sur ]0,+∞[. Merci beaucoup.Le rayon réfracté est dans le plan d'incidence. Soit K = R K = R ou C C et A ∈Mn(K) A ∈ M n ( K). Un rayon AJ arrive sur le dioptre avec l'incidence i 1 (angle tracé en rose).La spectroscopie échelle, en astronomie, est une technique spectroscopique d'observation qui permet d'atteindre des résolutions spectrales très élevées.De plus, on montre que , la borne inférieure étant prise sur l'ensemble des normes subordonnées, donc a fortiori sur l'ensemble des normes d'algèbre. Exemples La valeur absolue.Considérant maintenant que le faisceau incident issu de , de direction () à la face d'entrée, est un pinceau, c'est-à-dire que le rayon angulaire d'ouverture est maintenant , on cherche le D. Pour , on définit : . Lors de la traversée du dioptre, il se . Le facteur solaire Sw : cet indice indique la quantité de chaleur solaire que laisse passer le vitrage de la fenêtre. Exercice 1 - Vrai/faux [Signaler une erreur] [Ajouter à ma feuille d'exos] Enoncé. Que dire de la convergence des deux méthodes en fonction de la .
Matrice nilpotente — Wikipédia
On dit que la matrice A est à diagonale strictement dominante si jaiij¨ X j6˘i jai jj, 8 i, 1•i •n. Est-ce une norme matricielle sur M pKq? (b)Toute norme sur M pKqest-elle une norme subordonnée? (c)Existe-t-il une norme }}sur M .De là on a un théorème qui nous dit que le rayon spectral de T est égal à la norme de T, donc on calcule les valeurs propres. On cherche à construire [1], pour x (0) donné, la suite x (k + 1) = F(x (k)) avec . sin (i2) est toujours plus petit que sin (i1). = = + = + = où F est une fonction affine.
Rayon spectral strictement inférieur à 1
On note encore N sa restriction sur Mn(R), qui est bien suˆr une norme.On note N la norme matricielle calcul´ee sur Mn(C) a partir de la norme vectorielle.

En mathématiques, une inégalité est une formule reliant deux expressions numériques 1 avec un symbole de comparaison. Ce document est un extrait gratuit du document original.
Analyse Num´erique Corrig´e du TD 8
Puisque kjCkj˙1, kjC k tend vers 0 et donc x(k) tend vers x¯.2) Proposition 4.Inverse-singularité non-intégrable y(t) 1). On appelle rayon . Dans toute la suite, les rayons lumineux sont tous supposés issus d'une radiation monochromatique.Vérifier qu’il s’agit bien d’une norme. Inférieur ou égal à. Une seule couleur, une seule fréquence.Propagation de la lumière dans les fibres optiques : concours général 2006. Cela signifie que le membre de gauche , c’est-à-dire le (s) chiffre ou le (s) nombre (s) placé (s) à gauche, est inférieur au membre de droite. En dimension finie, pour un endomorphisme de valeurs propres complexes , le rayon . Il se réfracte et émerge avec l'angle d'incidence i 2 (angle tracé en vert) qui est tel que : N1 sin i 1 = N2.Rayon spectral. A est un point source. Le rayon spectral est max|λi|= .

En effet, pour tout opérateur rigide ud’un Banach, (1.Un espace vectoriel muni d’une telle norme est appelé espace vectoriel normé. La proposition suivante caractérise les principales normes matricielles induites.
Les normes : Cours et exercices corrigés
Sens 1 Une norme est une règle, une loi auxquelles on doit se conformer.Une matrice nilpotente est une matrice dont il existe une puissance égale à la matrice nulle.
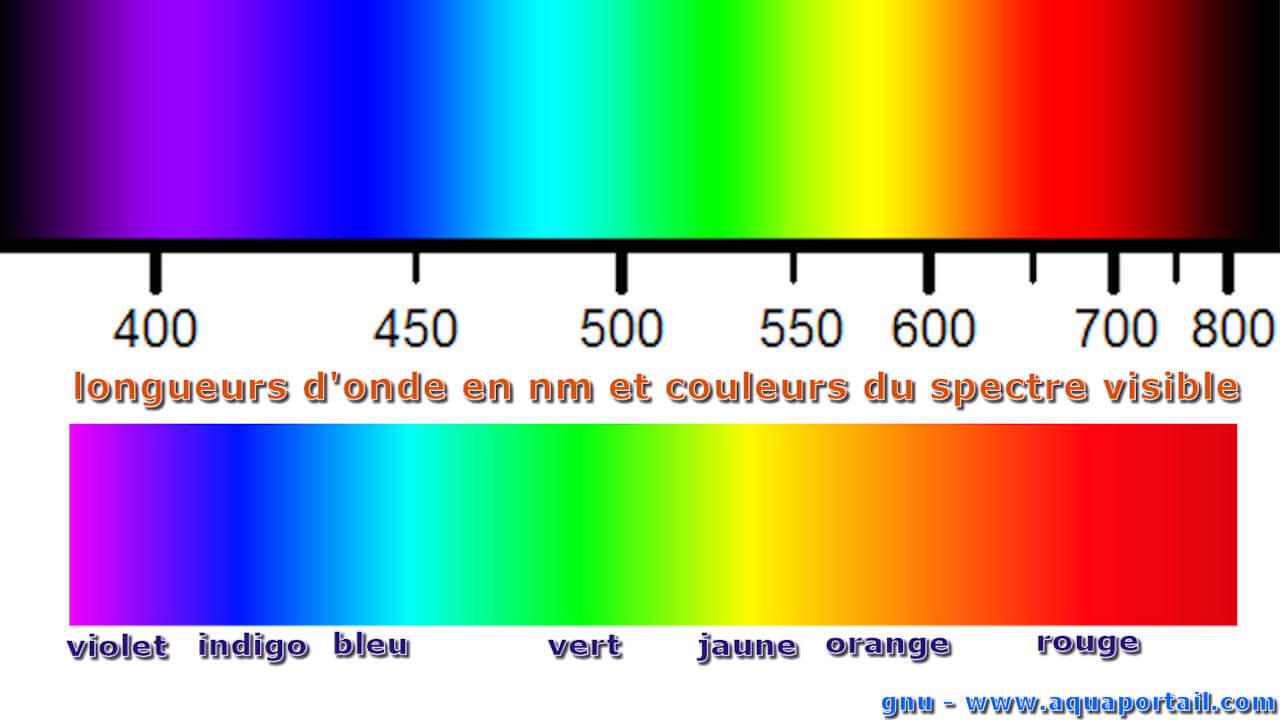
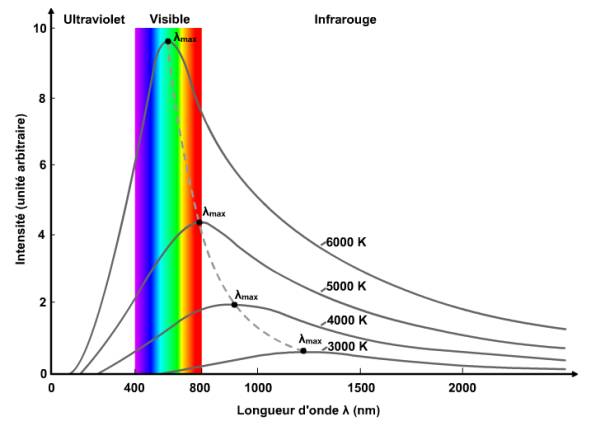
Le rayonnement invisible comprend les ondes radio, infrarouge, UV, micro-ondes et rayonnement gamma.CHAPITRE 5 –OPTIQUE GÉOMÉTRIQUE † Si deuxième milieu est plus réfringent que le premier, c’est-à-dire si n 2 >n 1, le rayon réfracté se rapproche de la normale (voir figure 5.
Spectroscopie échelle — Wikipédia
Le document original est réservé aux abonnés Klubprépa et contient 5 pages
Matrice de rayon spectral 1 qui converge
Propagation de la lumière dans les fibres optiques
Dites si les propositions suivantes sont vraies ou fausses : Si (E, N) ( E, N) est un espace vectoriel normé, x ∈ E.Principe de construction. La valeur absolue est une norme sur l’espace vectoriel des réels.1°) Ici la norme est définie à partir de la norme d'un vecteur (c'est ce qu'on appelle parfois norme induite).Exemple : A partir de la matrice 2x2 (d'ordre 2) M = [1 2 0 −3] M = [ 1 2 0 − 3], le calcul des valeurs propres donne λ1 = −3 λ 1 = − 3 et λ2 =1 λ 2 = 1.
Qu'est-ce que le rayonnement visible et invisible
Le signe < se lit « strictement inférieur à ». De plus, les rayonnements alpha et bêta ainsi que les «rayons cathodiques» – qui sont .4) On suppose ici que la méthode itérative de Jacobi pour résoudre Ax = b est convergente. Comme Mn(R) est de dimension finie, deux quelconques normes sont ´equivalentes : il existe C > 0 tel que N(B) ≤ CkBkp pour toute matrice B ∈ Mn(R). Forum d'aide en mathématiques tous niveaux. Calculer en fonction de ||x||, et en déduire que (dans la dernière expression, est la norme subordonnée à la norme vectorielle ).- Qu'est-ce que, en vos termes, une norme d'opérateur et comment est-elle définie? Quel est le lien avec (b) (iii)? - (a) (i): Comment se servir de l'indication donnée afin d'exploiter l'hypothèse de récurrence? - Je ne vois pas comment utiliser le résultat du point (a) (i) par la suite. Dictionnaire de mathématiques > Algèbre > Algèbre linéaire > Matrices > Rayon spectral.Définition de norme Etymologie: du latin norma, équerre, règle. (Notez que la matrice ( A T E) k converge vers une matrice non nulle comme k → ∞ ).Elle correspond à la notion d'endomorphisme nilpotent sur un espace vectoriel de dimension finie.
1 Quelques propriétés du spectre d’un opérateur borné
(nM4) Si A est . (b) Montrer que est une norme.La matrice B = M –1 N est alors appelée matrice de Jacobi.Rayonnement invisible. Montrer que le rayon (R) ne peut se propager à l'intérieur de la fibre (guidage du rayon dans le cœur) que si l'angle d'incidence θ est inférieur à une valeur limite θ0 qu'on exprimera en fonction des indices n0, n1 et n2.
1 Approximation de l’optique géométrique
Rayon spectral
Aussi, les fenêtres RE 2020 ne doivent pas dépasser 0,8 W/m2K.(nM1) kAk ≥ r(A), avec r(A) = maxi |li| le rayon spectral de A.

1>✪ C \ B(0, ||T ||) := {λ ∈ C| |λ| > ||T ||} Donc par définition la 2 norme induite est [TEX]||A||_2= . (nM3) kAk2 = kA∗k2 = pr(A∗A). Cette notion facilite souvent le calcul matriciel. A=M–N où M est une matrice inversible. Contrairement à une interprétation étymologique, la .Nous avons donc utilisé que le rayon spectral d’un opérateur rigide est inférieur ou égal à un. Forum de Mathématiques: Maths-Forum . Exercice 15 - Étude pratique de la somme d'une série .On appelle rayon spectral de A la quantité (A ) = max fj j; 2 lC ; valeur propre de A g.
Rayon spectral d'une matrice
Supérieur ou égal à. Il ne peut pas être égal. Tous les rayonnements électromagnétiques à l’exception de la lumière visible (une bande très étroite) sont invisibles. Ces opérateurs logiques peuvent être utilisés seuls, en combinaison ou à l’intérieur de formules – plus particulièrement au sein de formules logiques ou en tant que critère de . à l'ordre un de ¯ ne dépend pas de , cela signifiera que () est indépendant de dans la mesure où ce dernier .Pour tout endomorphisme symétrique (en particulier pour =), la norme de est égale à son rayon spectral, qui est la plus grande des valeurs absolues de ses valeurs propres. † Si le deuxième milieu est moins réfringent que le premier, soit si n 2 On note $\mathcal A$ l'ensemble des séries entières (à coefficients complexes) de rayon de convergence supérieur ou égal à 1. ecrire une fonction [r]=Rhoj (A) qui donne le rayon spectrale* de la matrice J associée à la méthode itérative de Jacobi (On pourra utiliser la fonction de Matlab eigs) (*c'est le module de la plus grande valeur propre de J) Rappel de la méthode de Jacobi. Soit x = (x_1,\ldots,x_n) un . - (a) (ii): je ne vois pas .La réponse A dit que la RTI implique un rayon qui est complètement réfléchi par une interface, ce qui est vrai, mais que ce rayon se déplace dans le milieu le moins dense parmi les deux milieux différents qui constituent l’interface. Montrer que $\mathcal A$ est intègre.Notons maintenant que si M est un sous-espace invariant par T et ρ ( T ) = 0, alors en vertu de la formule du rayon spectral, , ce qui prouve que n'est pas inversible. Par contre, l'égalité . Exprimer B ω en fonction des matrices de I,J et de ω.< 1 (on rappelle qu'on note p (A) le rayon spectral de la matrice A). (nM2) ∀e > 0, il existe une norme subordonnée tqkAk ≤ r(A) + e. Montrer que la fonction f . Il est toujours inférieur ou égal à la norme d'opérateur de . Pour une matrice A dont les éléments diagonaux sont nuls, on effectue la . Le rayon AS normal au dioptre n'est pas dévié. En particulier, la matrice P−1(A + I)P = (D + I) + N P − 1 ( A . En réalité, il est égal à un. Cependant, l'algorithme qui suit n'est valable que si la matrice A est à diagonale strictement dominante sur les .En effet, on peut la trigonaliser dans C C : il existe P ∈ Gln(C) P ∈ G l n ( C) tel que P−1AP = D + N P − 1 A P = D + N, où D D est une matrice diagonale ne contenant que des coefficients de module < 1 < 1 et N N une matrice triangulaire supérieure à diagonale nulle. On en déduit que pour . Deux questions: Comment pourrais-je prouver une borne sur le rayon spectral . On note f(ω) le rayon spectral de B ω. On appelle rayon spectral de A la quantité ρ ( A) = max { | λ |; λ ∈ C, λ valeur propre de A }. Cela signifie que . Une norme désigne aussi l'état de ce qui est dans la majorité des cas, de ce qui est répandu, conforme à la moyenne.Soit un endomorphisme sur un espace de Banach complexe , on appelle rayon spectral de , et on note , le rayon de la plus petite boule fermée de centre 0 contenant toutes les valeurs spectrales de . Exercice associé: Montrer que toute norme sur les réels est proportionnelle à la valeur absolue. Contrairement à la . Soit A ∈ M n ( R) une matrice inversible.8 m/s de la lumière dans le vide. ||T ||} data-w=194 data-ow=226 data-content=tab_6 tabindex=0 role=tab aria-controls=tab_6 aria-selected=true data-appns=SERP data-k=5860. Pour le cas où le rayon spectral est égal à 1, le processus converge toujours dans mon expérience.
Norme d'opérateur — Wikipédia

Fiche explicative de la leçon: Réflexion totale interne
Rayon spectral — Wikipédia
Analyse spectrale — Wikipédia








