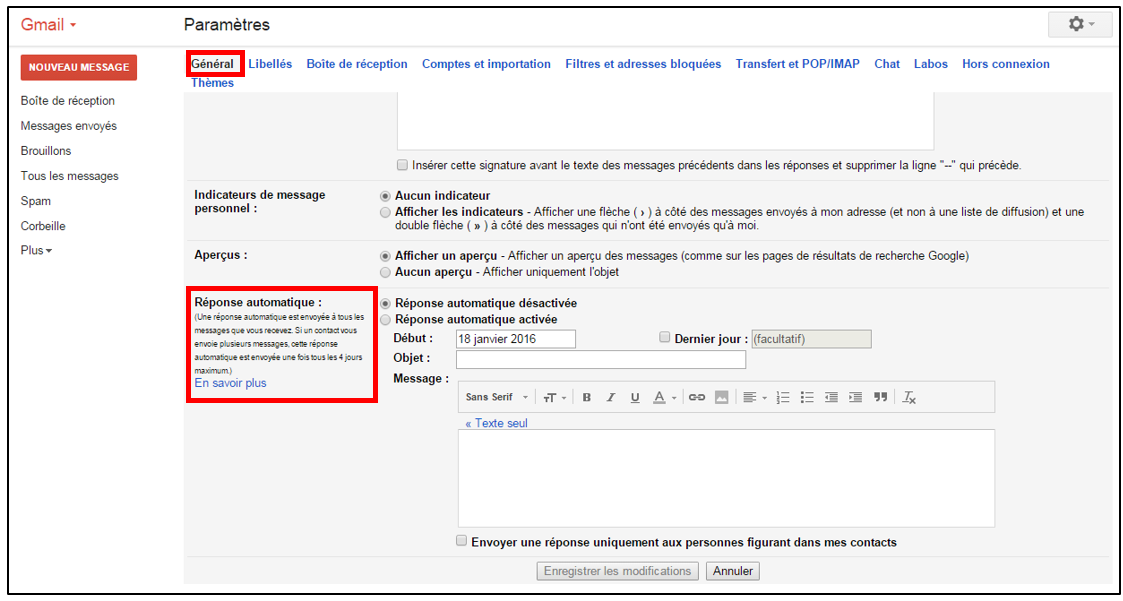
First order odes pdf
Lecture 24: Introduction to First-order Systems of ODEs
For our example, y . But most importantly for us right now, there is a method for solving linear first order equations. \ [F\left (y^ {\prime}, y, x\right)=0 \nonumber \] There are two common first order differential equations for which one can . A linear rst-order equation can be expressed in the form.1) the following form with the left‐hand‐side (LHS)Consider the response of a first-order ODE model: τdy ( t) dt + y(t) = u(t) to a step forcing function. Example 2: x d2y dx2 + dy dx + xy = 0 arises in . First Order ODEs. Such ODEs can be solved by direct integration: Write dy . By re‐arranging the terms in Equation (7.
First Order ODEs
Taille du fichier : 1MB
Math 353 Lecture Notes First order ODEs: exact equations
Differential Equations
The 4th
A scalar ODE will be given geometric interpretation and thereby try to gain a geometric understanding of solution structure of ODE whose vector field has some invariance. A 100 gallon tank is initially full of fresh water.ODE Steps for First Order ODEs Overview Examples Overview This help page gives a few examples of using the command ODESteps to solve first order ordinary differential equations.1 First-order ODE; Initial value problems We consider an ODE in the following standard form: y0(t) = dy dt = f(t;y); t2[a;b]; y(t) 2Rd where fis a function f: [a;b] Rd!Rd. We take a linear combination of these solutions to find the general solution. The differential equations in . Integrating the last equation in our example, Z d dx [x4y] dx = Z x6 dx ֒→ x4y = 1 7 x7 + c . From: Mathematics in . We indicate that we can formally obtain solutions, as one can . Authors: Carlos Enrique. g(y) = h(x) dx. WONG (FALL 2018) Topics covered.MATH 353 LECTURE NOTES FIRST ORDER ODES (THEORY AND QUALITATIVE BEHAVIOR) J.First-Order Linear Equations.1) in which h(u) and g(x) are given functions. The first is the separable case and the second is a first order equation. Learn the definitions of .1) y ˙ + p ( t) y = 0. WONG (FALL 2019) Topics covered. Instead, we will motivate the study of exact equations by making a detour into . First-order Ordinary Differential Equations and Applications.MATH 356 LECTURE NOTES FIRST ORDER ODES: FIRST ORDER ODES AND SOME FUNDAMENTALS.3 First order linear ODEs Aside: Exact types An exact type is where the LHS of the differential equation is the exact derivative of the product.This page titled 21. These two categories are not mutually exclusive, meaning that some equations can be both linear and separable, or neither linear nor separable. • We will have a slight change in our notation for DE’s. We note that the characteristic equation is.A first order differential equation takes the form.2: 1st Order Ordinary Differential Equations We will discuss only two types of 1st order ODEs, which are the most common in the chemical sciences: linear 1st order ODEs, and separable 1st order ODEs.
Solving First Order ODEs Table of contents
For example, the solution exists wherever \(p(x)\) and \(f(x)\) are defined, and has the same regularity (read: it is just as nice).Often, a first-order ODE that is neither separable nor linear can be simplified to one of these types by making a change of variables. Instructor/speaker: Prof.1: First Order Differential Equation.Solutions of linear equations have nice properties.1 Background/context. Existence and uniqueness of .Basic concepts. ODEs that reduce to exact ODEs. We introduce basic concepts of theory of ordinary differential equations. The trick is to rewrite the left hand side of \(\eqref{eq:1 .Nous voudrions effectuer une description ici mais le site que vous consultez ne nous en laisse pas la possibilité. Note that the . (1) As fcan be nonlinear in y(say f(x,y) = xy2), we are not restricted to linear ODEs.
Linear First-Order Equations
In today’s lecture we’re going to examine another technique that can be useful for solving first-order ODEs. Mixing Problems Consider the following situation.
ORDINARY DIFFERENTIAL EQUATIONS FOR ENGINEERS
View PDF HTML (experimental) Abstract: A new class of vector fields enabling the integration of first-order ordinary differential equations (ODEs) is .108 Linear First-Order Equations 4.
This chapter is dedicated to using numerical methods to solve initial-value problems (IVPs) of ODEs. We will limit our focus to first-order diferential equations, in particular to initial value problems of the form. Separation of variables form.
Ordinary Differential Equations
y˙ + p(t)y = 0 (17. First Order Equations We start our study of di erential equations in the same way the pioneers in this eld did. • We will only discuss first order systems. erx, xerx, x2erx, .Given a first-order ordinary differential equation (dy)/(dx)=F(x,y), (1) if F(x,y) can be expressed using separation of variables as F(x,y)=X(x)Y(y), (2) then the equation can be expressed as (dy)/(Y(y))=X(x)dx (3) and the equation can be solved by integrating both sides to obtain int(dy)/(Y(y))=intX(x)dx.Download Free PDF.2 Lie Symmetries of First-Order ODEs; 3 How to Find Lie Point Symmetries of ODEs; 4 How to Use a One-Parameter Lie Group; 5 Lie Symmetries with Several Parameters; 6 Solution of ODEs with Multiparameter Lie Groups; 7 Techniques Based on First Integrals; 8 How to Obtain Lie Point Symmetries of PDEs; 9 Methods for . Peano [244] and in 1915 by O. First‐order ODEs. LECTURE 9 Applications of First Order ODEs 1. By applying the Laplace transform with initial conditions: y(0) = y0, we obtain an algebraic equation: τ(sy(s) − y0) + y(s) = u(s) We assume a unit step input u(t), where u(s) = 1 s; then, the output is solved as: y(s) = 1 s(τs + 1 . The simplest first order ODE is y′ = g(x). Here are some important examples: Homogeneous Equation of Order 0: dy dx = f(x, y) where f(kx, ky) = f(x, y). In general a first order ordinary differential equation (ODE) is of the form: (13.2)y′(x) = f(x, y) where f(x, y) is some function, which can in general have x and y dependance. This is a textbook targeted for a one semester first course on . Before, in Chapters 1–4, we used the letter x for the independent variable . Use the change of variables z = y x to convert the ODE to xdz dx = f(1, z) − z, which is separable. Solve the system of first-order ODEs: sin 2 cos y 1 sin x y dx 1 dy sin 2 cos x y dx 2 dy Subject to the initial conditions: y1 0 1 and y2 0 1 Solve the ODEs in the interval: 0 ≤x ≤20 using 100 intervals.In the spirit of the second order solution, and for the same reasons, we have the solutions.2) y ˙ = − p ( t) y.3 Order n of the DE An ODE is said to be order n, if y(n) is the highest order derivative occurring in the equation.netChapter 2 First Order Differential Equationsmath. for some functions g(·) and h(·).
ISBN: 978-620-2-79841-9.
Manquant :
The first type of such ODEs that we will consider is the following: Definition Separable variables: A first order differential equation of the form dy dx = g(x)h(y) is called separable or to have separable variables.
To these {\\it linear} symmetries one can associate an ODE class which embraces all first order ODEs mappable into separable through linear .1: Scalar First-Order Linear ODEs is shared under a CC BY-NC-SA 4. Systems of First Order Linear Differential Equations. or equivalently. This is a textbook targeted for a one semester first course on differential equations, aimed at engineering students. y′(t) = f(t, y(t)) (1) y(t0) = y0. We will introduce the ideas and terminology of superposition, systems, input and response which . A solution of a first order differential equation is . NAGY { ODE August 16, 2015 1 Chapter 1. Note that the standard ODE solvers for MATLAB require you to input a rst-order ODE in standard form, so you will need to carry out this transformation before using it. Publisher: LAP LAMBERT Academic Publishing. For first order ODE, existence of such extremal solutions were already studied in 1885 by G.eduRecommandé pour vous en fonction de ce qui est populaire • Avis
Chapter 7 First-order Differential Equations
However, setting an initial condition does not necessarily guarantee the existence of a unique solution.FIRST ORDER ODES II 7 If y0>0 then y(t) increases (move to the right) If y0<0 then y(t) decreases (move to the left) If y0= 0 then y(t) stay constant.
(PDF) Handbook of Ordinary Differential Equations: Exact .Book PDF Available.FIRST ORDER ODEs §6.First order ODE s We will now discuss different methods of solutions of first order ODEs. y ( 4) − 3y ‴ + 3y ″ − y ′ = 0.su ces to derive methods for rst-order ODE’s.1 First-order diferential equations.
(PDF) Applications of First-Order ODEs
Integrate with respect to x both sides of the last equation obtained, Z d dx [µy]dx = Z µ(x)f (x)dx ֒→ µy = Z µ(x)f (x)dx .
Session Overview. However, it should .The order of a differential equation is the order of the highest derivative of the unknown function (dependent variable) that appears in the equation. Prerequisite for the course is the basic calculus sequence.An algorithm for solving first order ODEs, by systematically determining symmetries of the form [ xi = F(x), eta = P(x) y + Q(x) ], where xi d/dx + eta d/dy is the symmetry generator - is presented. We note that y1 = C1ex is the general solution of the first equation.These are homework exercises to accompany Libl's Differential Equations for Engineering Textmap.E: First order ODEs (Exercises) These are homework exercises to accompany Libl's Differential Equations for Engineering Textmap. For the purely mechanical treatment of exact equations, see the textbook. A first order differential equation is an equation of the form \(F(t, y, \dot{y})=0\). In this session we will start our study of linear equations, which is probably the most important class of differential equations.Topics covered: Introduction to First-order Systems of ODE’s; Solution by Elimination, Geometric Interpretation of a System. For the best experience, we recommend viewing online help using Google .Learn to solve typical first order ordinary differential equations of both homogeneous and non‐homogeneous types with or without specified conditions.First-Order ODE: Separable Equations, Exact Equations and Integrating Factor Department of Mathematics IIT Guwahati SU/KSK MA-102 (2018) REMARK: In the last theorem of the previous lecture, you can change the open interval (a;b) to any interval I(Imay be open or closed or semi-closed, it does not matter). a1(x) + a0(x)y = b(x) 1 dx where a1(x) a 0(x) and b(x) depend only on the independent . Take the first order system. Depending on the properties of .A first order homogeneous linear differential equation is one of the form.As illustrated above, the general solution of first-order ODEs depends on an arbitrary inte-gration constant that must be specified with an additional condition. As we just discussed, it is reasonable to refer to ‘the solution’ y(t) through y 0 because the initial time t 0 does not matter (only true for autonomous equations!). Sometimes a system is easy to solve by solving for one variable and then for the second variable.The 4th -order Runge-Kutta method for a system of ODEs-----By Gilberto E. Of all the techniques for solving first order ODEs, separation of variables is the simplest to . y˙ = −p(t)y. Linear'' in this definition indicates that both y˙ y ˙ and y y occur to the first power; homogeneous'' refers to the zero on the right hand . The theorem is given in its . Specifically, we will evaluate their accuracy and efficiency. \ [F\left (y^ {\prime}, y, x\right)=0 \nonumber \] There are two common first order differential equations for which one can formally obtain a solution.
Chapter 1 First‐order ordinary differential equations (ODEs)
However higher order systems may be made into first order systems by a trick shown below. See Student[ODEs][ODESteps] for a general description of the command ODESteps. Basic de nitions and . x dy dx +y = ex . It is then ‡ushed out with a salt solution coming in at a concentration of 1/2 lb/gal and at a rate of 2 gal/min. in which all dependence on x and dx has been separated onto one side of the equation with all dependence on y and dy on the other. Example 1: dP dt = kP, for k > 0, describes the size P of a population at time t under the assumption that the growth rate is proportional to the existing population. Introduction A differential equation is an equation involving an unknown function and one or more of its derivatives.The most general 1st order ODEs we will study are of the form y′ = f(x,y).
