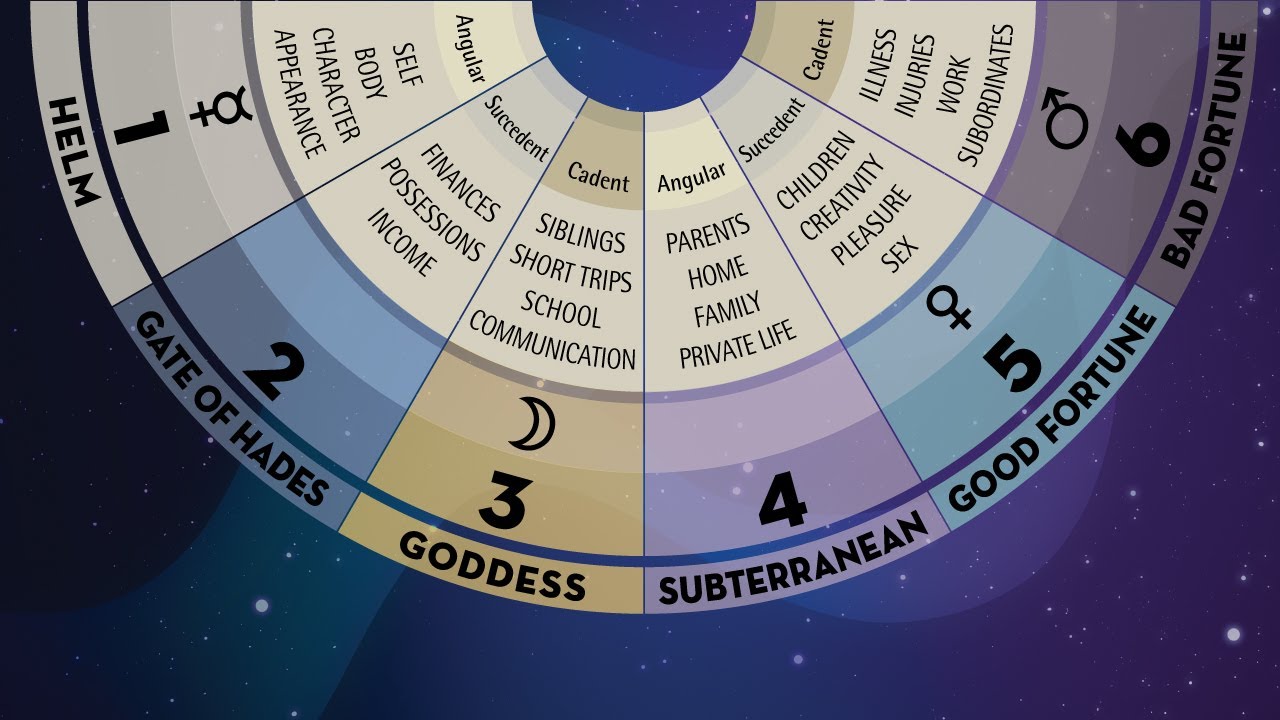
Formule somme de ramanujan

Le réel est appelé raison de la suite.Dans ce carnet de route : des séries divergentes, des carnets de Ramanujan, et de l’électromagnétisme dans le vide.Je ne connais aucune démonstration de cette formule, quand la somme infinie du premier membre a la signification habituelle.La formule (2)(a) s’étend à une somme de termes dont le nom bre est visible dans le contexte c , la formule (2)(b) à un produit de facteurs dont le nombre est visible dans le con teste c .
zêta(x)=(Somme de n=0 à l’infini) 1/(n^x)) n’est qu’une définition possible de la fonction zêta seulement si la partie réelle de x est supérieure à 1 ! Ce n’est cependant pas le cas pour -1, donc on ne peux remplacer x par -1 dans cette formule.de Ramanujan Édouard Thomas Revue Tangente Kafemath du jeudi 19 janvier 2012 La coulée douce 51 rue du Sahel 75012 Paris. 2 Srinivasa Ramanujan (1887–1920) • Un . December 2017 dans Analyse.Temps de Lecture Estimé: 10 min
1 + 2 + 3 + 4 + ⋯ — Wikipédia
La fonction ˝ de Ramanujan.Ensuite, à propos du prolongement analytique de Ramanujan pour calculer la somme de la série des entiers naturels, aussi appelée somme de Ramanujan.Équation de Ramanujan-Nagell. [ S'agissant d'un nom propre (Srinivâsa Aiyangâr Râmânujan), on s'efforcera de l'écrire comme il se doit, sans . La fonction Zêta de Riemann prend bien la valeur -1/12, mais ce n'est plus une valeur d'une série. Fascinant et mystérieux, il est mort jeune en laissant des milliers de formules non .PDF | On Jan 19, 2023, Daniel Parrochia published Sur quelques formules de Ramanujan | Find, read and cite all the research you need on ResearchGate (1887-1920) La vie du mathématicien indien Srinivasa Ramanujan représente un cas pratiquement unique dans l'histoire des mathématiques.

Bien qu'il ait montré des .
Les mystérieux carnets de Ramanujan
C'est un sujet qui suscite des débats parmi les mathématiciens.La somme des premiers termes d'une suite arithmétique vaut : . La démonstration la plus simple n'est pas .jusqu'à l'infini = -1/12 En vous remerciant d'avance.Re : Somme de Ramanujan. \sum_ {k=0}^ {+\infty} k =- \dfrac {1} {12} k=0∑+∞ k = −121. En analyse, la sommation de Ramanujan est une technique inventée par le mathématicien Srinivasa Ramanujan pour donner une valeur aux séries infinies divergentes.Les formules de Ramanujan. Est-ce vraiment le cas ? Non, nous explique Benoît Rittaud, du moins pas dans le sens intuitif que revêt une expression telle que 1+2+3+4+. Huitième volet de la collection « Génies des mathématiques », l’Indien Srinivasa Ramanujan, sorte de supernova dont l’explosion a illuminé les moindres recoins des mathématiques.Bonus : Pour Ramanujan, on a. Seulement des pseudo-preuves où on remplace dans une formule un nombre par une valeur qu'il ne peut prendre. En plus des développements discutés dans cet article, les sommes de Ramanujan sont utilisées dans la preuve du .Théorème de Hardy-Ramanujan. Mathématique, Tome 341 (2005) no.La base de la théorie des séries divergentes de Ramanujan est constituée par la formule de sommation d'Euler-Maclaurin. Srinivasa Ramanujan est né dans une famille indienne très modeste.
Biographie de SRINIVASA RAMANUJAN (1887-1920)
La vidéo explique les calculs du grand mathématicien indien Srinivasa Ramanujan qui sont à l . question réponse.
Sommation de Ramanujan — Wikipédia
Somme des carrés des entiers. C'est un exemple d' équation diophantienne exponentielle, une équation à résoudre en entiers où l'une des variables .1 Institut de mathématiques, université Bordeaux-I, 351, cours de la libération, 33405 Talence cedex, France . Factorielle et exponentielle.1 729 est également connu sous le nom de « nombre de Hardy-Ramanujan » ; il s'agit du plus petit entier naturel s'écrivant de deux manières différentes comme somme de deux cubes 1 : Il s'agit donc du nombre taxicab d'ordre 2.RAMANUJAN Srinivasa Aaiyangar, indien, 1887-1920.Une sommation de Ramanujan, dans son premier cahier, montrant pourquoi la somme de tous les entiers est égale à -1/12. Admis en 1903 dans un collège . Bien que la sommation de Ramanujan pour des séries .
Sur quelques formules de Ramanujan
Srinivasa Ramanujan (1887-1920) avait appris tout seul les mathématiques, grâce à deux livres seulement.We study and try to explain the genesis of some formulas of continuous fractions from Ramanujan, which the author presented without demonstration, and without it being possible to know how he was able to obtain them. Nous supposerons connues les bases de la th eorie des formes modulaires (d e nition d’une forme modulaire de poids k 4 pair et de niveau 1). Mathématiques.
Conjecture de Ramanujan — Wikipédia
En fait, tous ces objets et autres théorèmes sont liés d'une façon ou d'une autre à l'une des formules énoncées par Ramanujan .

Maths Sans Stress

Deux exemples spectaculaires de la créativité de Ramanujan sont les formules suivantes : + = . Le nom de Srinivasa Ramanujan est malheureusement peu connu.
Partition d'un entier — Wikipédia
Pour être plus précis, Srinivasa . Cet autodidacte indien a pourtant révolutionné les mathématiques. , Prix Sastra Ramanujan. Interprétation : Il s'agit de la valeur de Zeta en -1.Ramanujan faisait preuve d’une extraordinaire mémoire des nombres et de leurs propriétés.(nombre qui est presque entier ), mais aussi aux identités de Ramanujan sur les fractions continues, au théorème de Ramanujan sur les formes quadratiques, et à environ 42 000 autres constantes de Ramanujan .La fonction sq hérite des sommes de Ramanujan1 une série de propriétés fondamentales : (i) Pour x ∈RZ ,onasq(x)+sq(−x)+ϕ(q)=0. On rapporte à ce sujet l’anecdote suivante, devenue célèbre: « Un .En analyse, la sommation de Ramanujan est une technique inventée par le mathématicien Srinivasa Ramanujan pour donner une valeur aux séries infinies divergentes. En mathématiques, et plus précisément en théorie des nombres, l' équation de Ramanujan-Nagell est une équation liant un carré parfait comme étant une puissance de deux moins sept. Très jeune, il est détecté comme . Fran˘cois Brunault. Cet article fait partie de la série CodeS-SourceS: Approximations de Pi. Cette méthode a été utilisée avec succès dans certains cas pour donner une valeur à des séries divergentes, mais elle ., serait égale à -1/12. C’est ici pour télécharger le fichier pdf, et là pour en savoir plus sur le séminaire de la . Nous étudions et tentons d’expliquer la genèse de quelques formules de
Une remarque sur les sommes de Ramanujan
Srinivasa Ramanujan.
Équation de Ramanujan-Nagell — Wikipédia
C'est le cas en particulier pour les approximations de Pi.Quelques formules (mais il y en a tellement.
Somme de Ramanujan
précision de dix décimales : + + = + précision de dix décimales : = + Cette approximation curieuse résulte de l'observation .
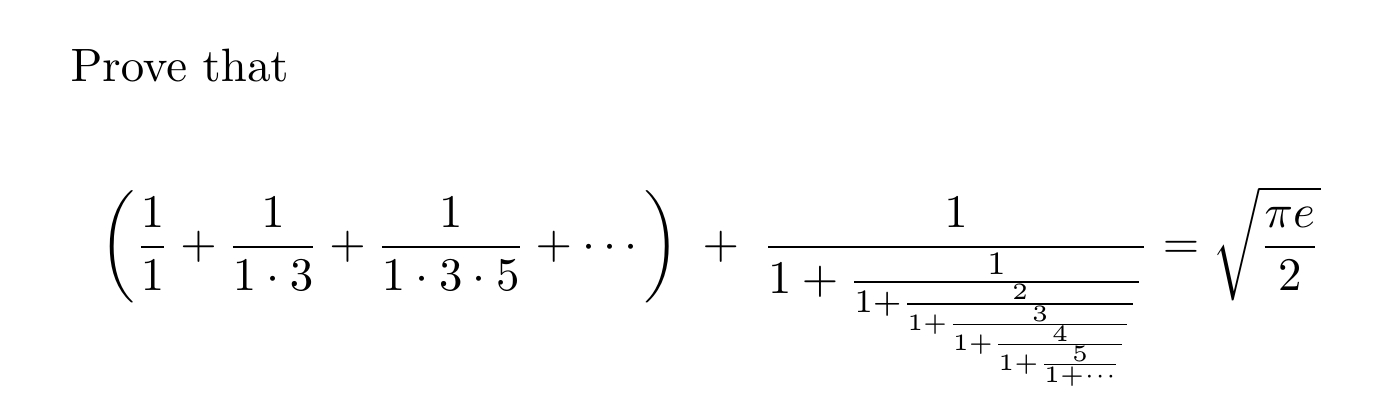
688 - Sur la notion de constante dans la théorie des séries divergentes de . Comme dans tous les articles de cette série, on se limite à la . — Non, me répondit-il, c'est un nombre très intéressant : c'est le plus petit nombre .
somme de factorielles
Cordialement, Dernière modification par StrangQuark ; 05/08/2021 à 09h22 . En mathématiques et plus précisément en théorie des nombres, le théorème de Hardy-Ramanujan 1, demontré par G.de Fourier suivant, que l’on peut obtenir gr^ace a la formule de sommation de Poisson : Gk(z) = Bk 2k + X1 n=1 ˙k 1(n)e 2iˇnz; (3) ou Bk d esigne le k-i eme nombre de Bernoulli . Srinivasa Ramanujan a mentionné les sommes dans un article de 1918. Bonjour, quelqu'un pourrait m'indiquer comment comprendre cette loi suivante: 1+2+3+4+. Bien qu'elle ait été découverte en 1657 par Bernard Frénicle de Bessy, la propriété de 1 729 ainsi que son . Le lecteur pourra se r ef erer a [Z] qui est De telles formules sont également des équations modulaires désormais .Srinivasa Ramanujan présente deux démonstrations de « 1 + 2 + 3 + 4 + ⋯ = −1/12 » au chapitre 8 de son premier cahier 2, 3, 4. Une telle partition est en général . Expos e au s eminaire des doctorants de th eorie des nombres de Chevaleret, le 18 mars 2003.En mathématiques, la conjecture de Ramanujan, due à Srinivasa Ramanujan (et démontrée par Pierre Deligne en 1973), prédit certaines propriétés arithmétiques ainsi que le comportement asymptotique de la fonction tau qu'il a définie. En fait ces résultats ont des racines historiques profondes, qui remontent à Euler, Wallis, Viète, et même Archimède.Temps de Lecture Estimé: 6 min
L'univers de Pi
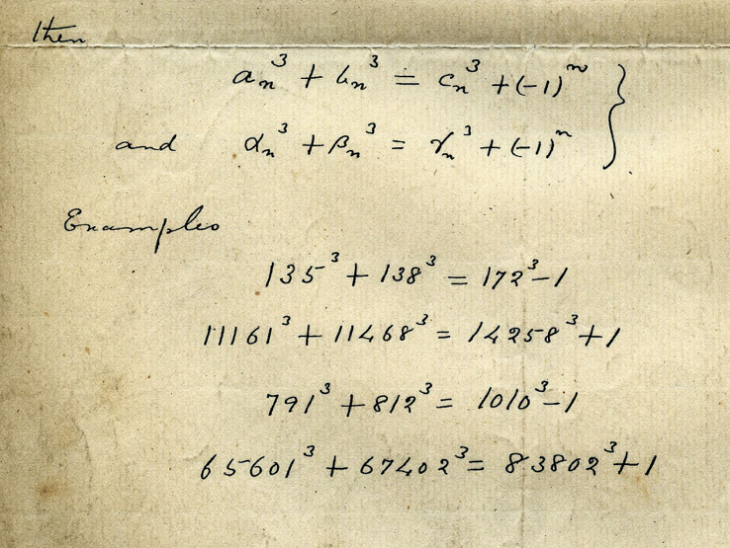
Mathématiques : de mystérieuses formules dues à Ramanujan enfin élucidées ! Peu avant sa disparition en 1920, le grand . Une suite est dite arithmétique si il existe un réel tel que pour tout . Un nombre entier étant donné, combien a-t-il de décomposition en somme d'entiers positifs ? Par exemple : 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = .Nous étudions et tentons d'expliquer la genèse de quelques formules de fractions continues de Ramanujan, que .Vue d’ensemble Possibilité de mise en facteurs et de mise en évidence de formules simples.

Eh bien pas ou sens où on l’entend, car la formule de la fonction « de base » (i.) En notant (x) n la valeur : (c'est le symbole de Pochhammer), on a : ouf ! Tranches de vie Avec Ramanujan, on touche à la quintessence de l'étude de Pi.Voici une des nombreuses formules de Ramanujan pour le calcul de pi: 1/pi = sqrt(8)/9801 * somme(i>=0) {(4*i)! * (1103+26390*i) / (i!)^4 / 396^(4*i)} Elle date de 1910 mais ne fut démontrée qu'en 1985.

:max_bytes(150000):strip_icc()/Simply-Recipes-Perfect-Cheesecake-LEAD-7-5a1aec38636245f090807026339d834b.jpg)