Function on a graph definition
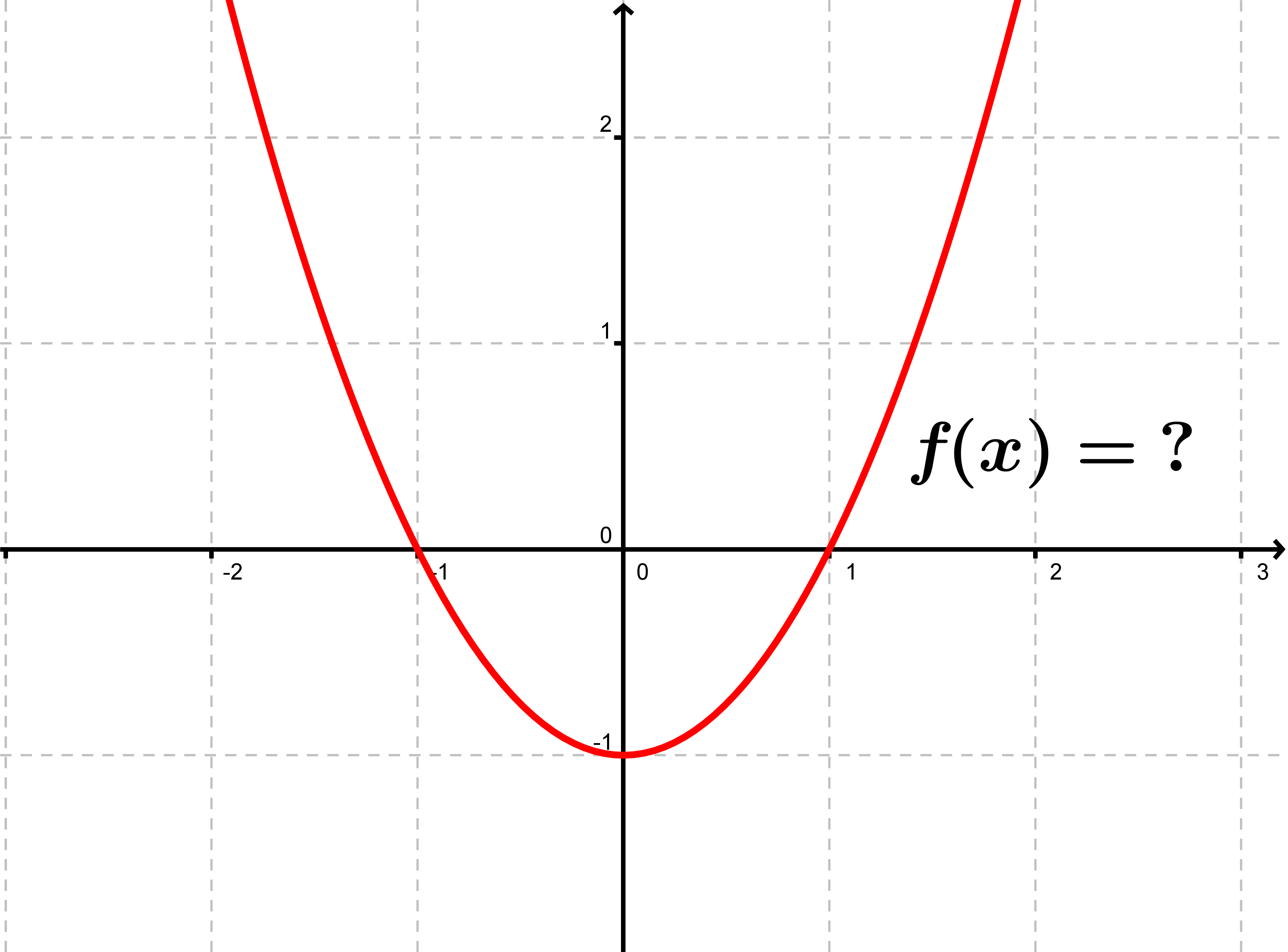
For example, the graph of the function f (x) = x 2 + 3 is obtained by just moving the graph of g (x) = x 2 by 3 units up.Explorez les mathématiques avec notre magnifique calculatrice graphique gratuite en ligne. Take for example, the function that maps each real number to its square. Intervals where a function is positive, negative, increasing, or decreasing.Graphing functions is drawing the curve that represents the function on the coordinate plane.A function is defined as a relation between a set of inputs having one output each.A function is the collection of all ordered pairs from such that .Why is it not a function? Help!If there is an x value that goes to two y values it is not a function. A linear function is a function that represents a straight line on the coordinate plane. Maxima will be the highest point on the curve within the given range and minima would be the lowest point on the curve.
1: Functions and Graphs
Note that input q and r both give output n.Function Transformations. The input values (x) of the function are plotted across the horizontal (x) axis. The corresponding point on the curve is the ., the graph of a discontinuous function breaks or jumps somewhere. In this case, each input is associated with a single output.
Desmos
A function is a relation where each input value (x-value) has only one output (y-value). It can be just a collection of points.Parent Functions and Parent Graphs.Graph the following rational function and identify any removable discontinuities. Definition: Point-Slope .Recognizing functions from graph (video) | Khan Academy.1 compares relations that are functions and not functions. Interestingly, the above functions have even powers.- Equation, Graph, Definition. Rational Function : A rational function is any function .orgThe graph of the function f is shown.1: Functions and Their Graphs.f(x)=sqrt(x) is a function. In symbols, we would write. Example 2 : Find the inverse function for the given function f (x) = 4x+ 1 3x− 2 4 x + 1 3 x − 2. Checking whether a given set of points can represent a . A function is generally denoted by f (x) where x is the input. Increasing, decreasing, positive or negative intervals (Opens a modal) Worked example: positive & negative intervals . are even functions. Graph f(x) = − 3 4x + 6 by plotting points. The graph of a function is the graph of all its ordered pairs, (x,y)(x,y) or using function notation, (x,f(x))(x,f(x)) where y=f(x). Quiz 2. The transformation of the graph is illustrated in Figure 3. This is also expected from the negative constant rate of change in the equation for the function.Identify Functions Using Graphs. There is one function that we’ve seen to this point that we . As we have seen in . Function transformations are very helpful .Extra: Well, if you are given an expression for h(a) which is not necessarily linear(that is not of the form of ax+b) then you can graph it computing various output points on various . If we name the function f, then f maps 5 to 25, 6 to 36, −7 to 49, and so on.Definition: Turning Points.What exactly is a relation and what is the difference between relation and a function?A relation is a set of ordered pairs. We also give a “working definition” of a function to help understand just what a function is. Definition: Slope of a Linear Function. Consider a trigonometric function (f(x) = cos x.
Identify a function. Before we can talk about writing the rule for a function using an equation, we must define a new .It's only the vertical line test that disqualifies it from being a function. If a curve (graph) represents a function, then every point on the curve satisfies the . So, graphing functions is pretty much the same as graphing equations. In simple words, a function is a relationship between inputs where each input is related to exactly one output.
Graph a function
Functions
Linear Function.Example 1 Sketch the graph of f (x) =(x−1)3 +1 f ( x) = ( x − 1) 3 + 1 . f(0) = A) f(-1) - Brainlybrainly.Graph of a function. We can see all the types of . Use function notation. Figure \(\PageIndex{4}\): Graph of a polynomial that shows the increasing and decreasing intervals and local maximum. Table of contents.heres another example: if a class is taking a test, the students would be the domain and the grades . Definition; Hole: A hole exists on the graph of a rational function at any input value that causes both the numerator and denominator of the function to be equal to zero. In the image given below, we can see various peaks .For example, we can use sets of ordered pairs, graphs, and mapping diagrams to describe the function. It is known that value is -1 because the − 1 is a constant.The graph of a function is the set of points in the Cartesian plane where the first coordinate is a value from the domain and the second coordinate is its corresponding . f = {(1, 2), (2, .The graphs of functions have the property that a vertical line can intersect them at most once, because otherwise it means that the same number has more than one image, not fulfilling the definition of a function.The range also excludes negative numbers because the square root of a positive number x is defined to be positive, even though the square of the negative number − √x also gives us x.A function that is NOT continuous is said to be a discontinuous function. We also define the domain and range of a function. In the sections that follow, we will explore other ways of describing a function, for example, through the use of equations and simple word descriptions.To use a graph to determine the values of a function, the main thing to keep in mind is that \(f(input) = ouput\) is the same thing as \(f(x) = y\), which means that we can use the \(y\) value that corresponds to a given \(x\) . Solution: We will use the inverse function formula (or steps to find the inverse function).
Functions and Graphs
The graph of h has transformed f in two ways: f(x + 1) is a change on the inside of the function, giving a horizontal shift left by 1, and the subtraction by 3 in f(x + 1) − 3 is a change to the outside of the function, giving a vertical shift down by 3. What is a parent function and what are the parent function graphs? Definition: A parent function is the most basic function from which a family of similar functions is derived. Expand/collapse global location. A graph is a picture that shows how sets of data are related to each other. For example, above is the graph of the function.1: (a) This relationship is a function because each input is associated with a single output. We introduce function notation and work several examples illustrating how it works.Functions Overview. The graph of a function is the collection of all ordered pairs of the function. By the definition of the continuity of a function, a function is NOT continuous in one of the following cases.Definition of the domain and range.
To locate the local maxima and minima from a graph, we .You use the vertical line test.
Manquant :
definitionIdentify Functions Using Graphs
If you can draw a vertical line any where in the graph and it crosses more than 1 point on the graph, then the grap.Definition: One-to-One Functions.20: Cube root function f(x) = 3√x. For example, y = 3x . In addition, the graph has a downward slant, which indicates a negative slope. A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). A polynomial of degree \(n\) will have, at most, \(n\) \(x\)-intercepts and \(n−1\) turning points. So this is one of the few times your Dad may be incorrect.
Manquant :
definition This observation provides an appropriate visual criterion for differentiating the graph of a function from other curves.For the function whose graph is shown in Figure \(\PageIndex{4}\), the local maximum is 16, and it occurs at \(x=−2\). In this case x=4 goes to y=-1 and y=5 Does that make sense?how do you recognize functions from graphs.Regarder la vidéo7:57A function, by definition, can only have one output value for any input value.well, if they have students with the same range, than why did anyone not notice that we have different domains? I'll let someone else think about t.An inflection point is a point where the graph of a function changes concavity from concave up to concave down, or vice versa.Manquant :
definition(vidéo)
Voici quelques exemples.In this section, we provide a formal definition of a function and examine several ways in which functions are represented—namely, through tables, formulas, and graphs.Explore math with our beautiful, free online graphing calculator. Google Classroom.Does it matter what cordinates you put the dots on?Yes. Learning Outcomes.If the equation is y = − 2 x − 1, the initial value is − 1.We could say that a function is a rule that assigns a unique object in its range to each object in its domain.Calculus (OpenStax) 1: Functions and Graphs.Recognizing functions from graph (video) | Khan Academykhanacademy. It is usually called . It’s easiest to understand this definition by . The graph of a function may not be a curve, as in the case of a real function. You have to put the dots on the specified. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. A circle can be defined by an equation, but the . These are usually represented as points in a Cartesian coordinate system. There's a lot of functions that don't pass the horizontal line test.Une fonction est un procédé qui permet d'associer à un élément d'un ensemble de départ, un élément unique d'un ensemble d'arrivée.

Linear Functions and Slope. Functions from Verbal Statements - turning word problems into . Determine the value of f(-x) and identify if it is an even function or not. If the problem wanted you to use the negative root, it would say - sqrt (x). The domain is all ???x???-values or inputs of a function and the range is all ???y???-values or outputs of a function. When we make a graph of a function, we are showing how its output changes as . A constant is a number that does not have a variable right next to . Every function has a domain and codomain or range. The range is all the values of the graph from down to up. In addition, we . 2) Select learner home 3) Then, click on your avatar to see options that you can c. When we make a graph of a function, we are showing how its output changes as we vary its input.
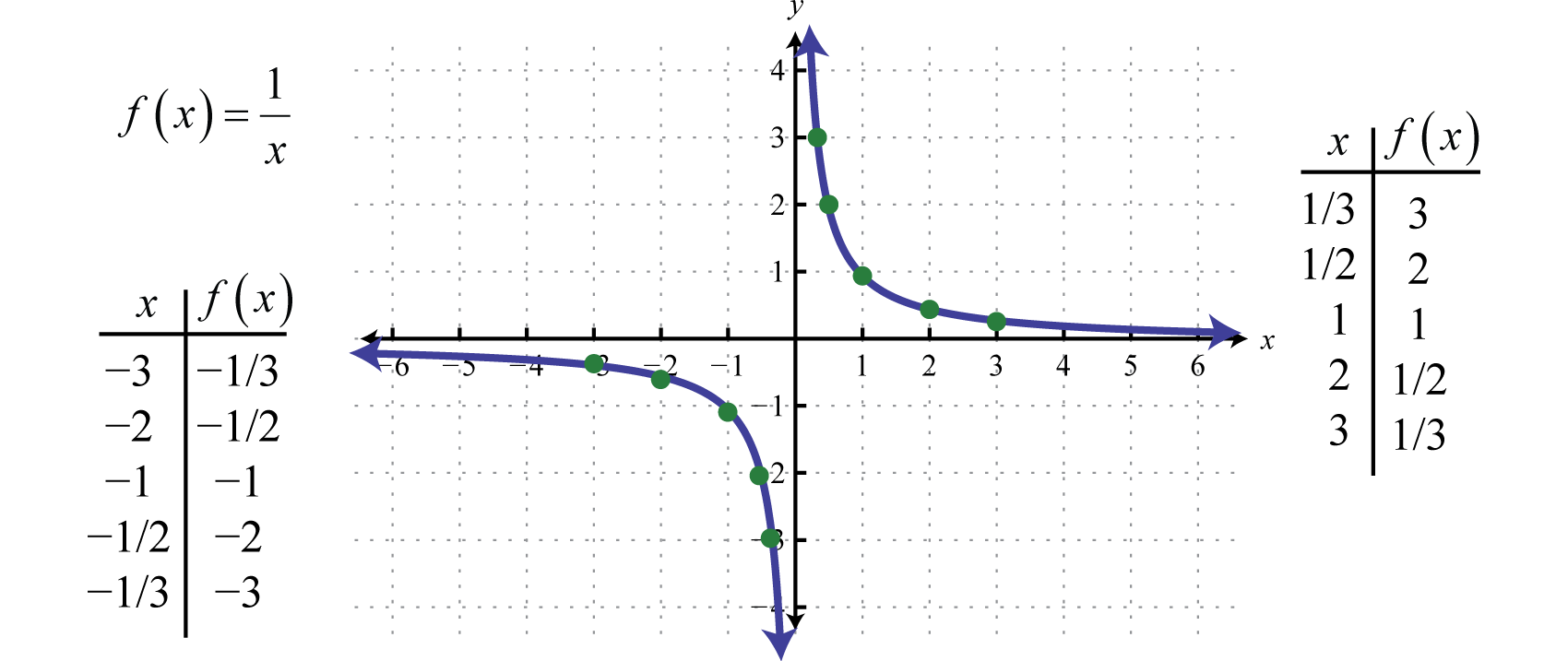
We can also display the images of a function in a table, or represent the function with an incidence matrix.It has two outputs; for example if we input 9 in we get -3 or positive 3. Example of an Even Function. Graphing a relation (a set of coordinates) can help determine if that relation is a function or not. Tracez des fonctions, des points, visualisez des équations algébriques, ajoutez des . Learn Practice Download.Similarly, functions like \(x^4, x^6, x^8, x^{10}\), etc. The local minimum is −16 and it occurs at \(x=2\).GRAPH OF A FUNCTION.I know a regular parabola is a function as it passes the vertical line test, but what about the hori. A function is a relation where every domain (x) value maps to only one range (y) value.1) Click on your name in the upper right corner of the screen.
Maxima and Minima
This section will help you prepare for more advanced topics in calculus and algebra.

What is a Function?
You will also explore the concepts of domain, range, intercepts, and symmetry of a function. Level up on the above skills and collect up to 320 Mastery points Start quiz.How do you change my profile picture. Learning Objectives.
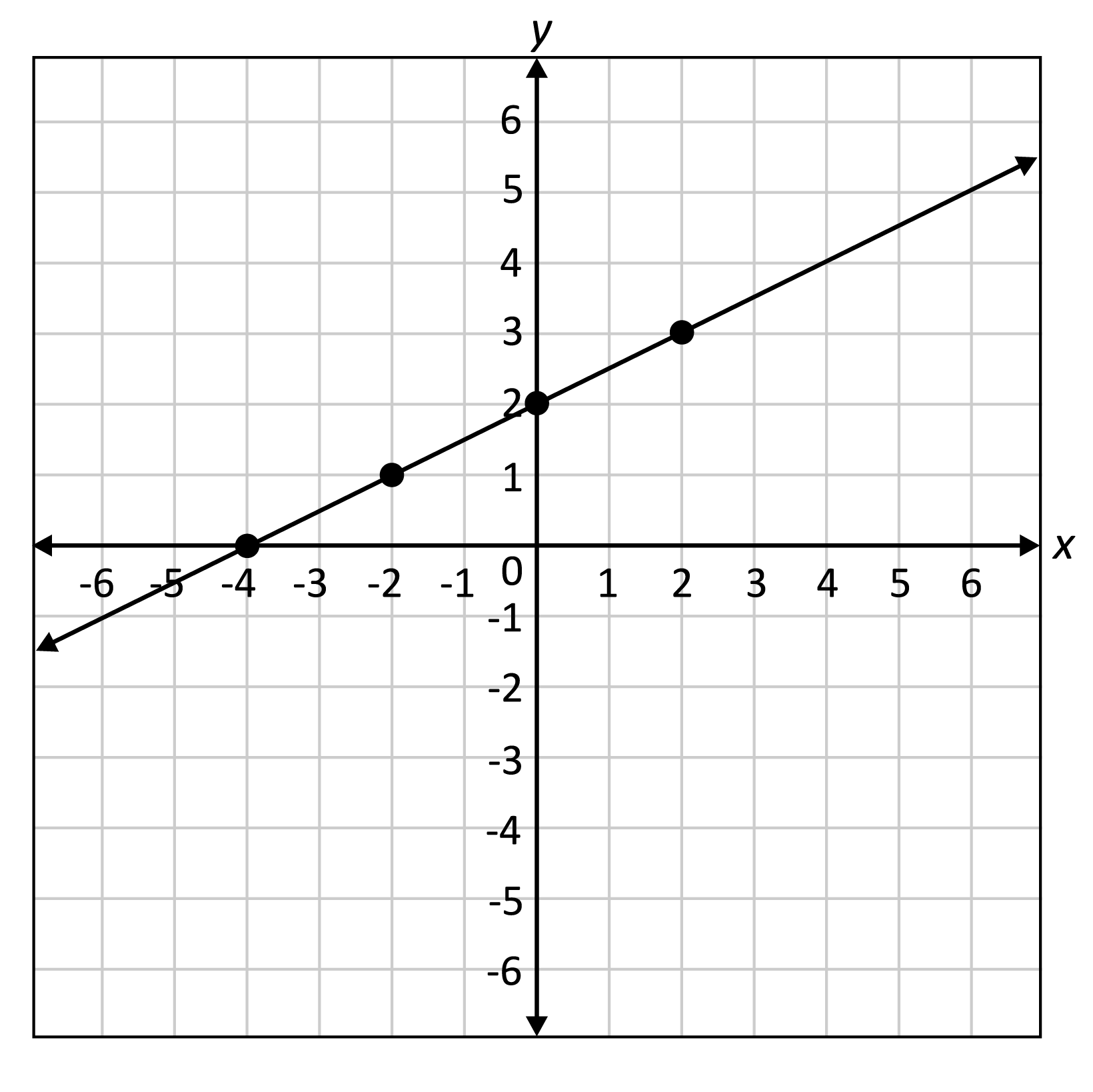
Graph of a function
In this section, we will start with the graph of a function, then make a number of interpretations based on the given graph: function evaluations, the domain and range of .
Recognizing functions from graph (video)
Observe the graph below y = x 2, an even function graph. If you input 9, you will get only 3. For the cube root function f(x) = 3√x, the domain and range include all real numbers. Let's explore how we can graph, analyze, and create different types of functions.If we change the axes, will it be a function?If we changed the points of the output, yes.By inverse function formula, f and g are inverses of each other. Since concavity is based on the slope of the graph, another way to define an inflection point is the point at which the slope of the function changes sign from positive to negative, or vice versa: Before the inflection . There are different types of discontinuities as explained below.In this section, you will learn how to graph a function using the Cartesian coordinate system, a powerful tool invented by Rene Descartes. Graphs, Relations, Domain, and Range. The given function is:1: Review of Functions. Remember, sqrt(x) tells you to use the principal root, which is the positive root.
Initial Value of a Function
comRecommandé pour vous en fonction de ce qui est populaire • AvisAuteur : Sal Khan
Inverse Function
\[\begin{array} {ll} {f} &{\text{name of function}} \\ {x} . Answer: We proved that f = g -1 and g = f -1. The transformation of the graph is illustrated in Figure 4. Identify the graphs of the toolkit functions. (b) This relationship is also a function. By performing various operations like addition, subtraction, multiplication, etc.
The graph of the function is a line as expected for a linear function.A graph is a picture that shows how sets of data are related to each other.Does this mean *f(x) = sqrt of x* is not a function? f (x)=sqrt (x) is a function. Verify a function using the vertical line test.










