Hamiltonian circuit algorithm
Complete graphs do have Hamilton circuits.Algorithm for Euler Circuits. An Euler circuit starts and ends at the same vertex.
Hamiltonian Circuit Algorithm
Algorithms to find Hamiltonian circuits. There are no loops or multiple edges in complete graphs.What is dynamic programming algorithm for finding a Hamiltonian cycle in an undirected graph? I have seen somewhere that there exists an algorithm with O(n.
Euler Circuit & Hamiltonian Path (Illustrated w/ 19+ Examples!)
A heuristic search algorithm is given that determines and resolves the Hamiltonian circuit problem in directed graphs.comThe Hamiltonian Cycle and Travelling Salesman Problems .
Hamiltonian Cycle
Hamiltonian Paths and Cycles (2) Remark In contrast to the situation with Euler circuits and Euler trails, there does not appear to be an efficient algorithm to determine whether a graph has a Hamiltonian cycle (or a Hamiltonian path). Modified 2 years ago. When the while loop is executed for row 3 of the array, the An Euler path ( trail) is a path that traverses every edge exactly once (no repeats). To do so, we will: Define a random set of weights over the hardware graph. Identify a connected . The algorithm is hardware-independent and reduces the overall circuit cost of Hamiltonian simulation, particularly by minimizing the number of CNOT gates. b) iterative improvement.Comme tous les solides de Platon, le dodécaèdre est représenté par un graphe hamiltonien. As a reminder, the algorithm consists of two parts: A Hamiltonian path: a .In this video, we work through an example using the sorted-edges algorithm to find a Hamiltonian circuit.
The solve() method of the Hamiltonian class is the recursive method implementing the backtracking algorithm.
En mathématiques, dans le cadre de la théorie des graphes, un chemin hamiltonien d'un graphe orienté ou non orienté est un .
Mathematics
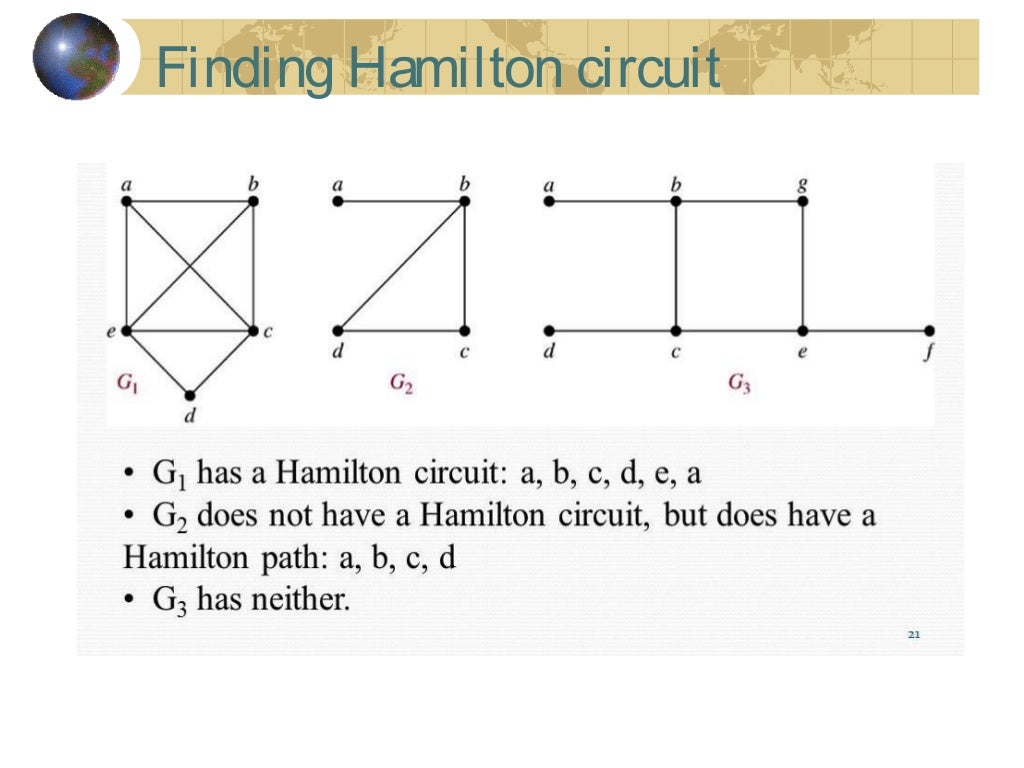
In each complete graph shown above, there is exactly one edge connecting each pair of vertices.Un cycle hamiltonien (en rouge) dans le graphe des arêtes du dodécaèdre. = 2 (nlogn) to try all possible permutations of the nodes (which can also be adapted to get an O?(k!)-time algorithm . In fact, it is the graph that Hamilton used as an example to pose the question of existence of Hamiltonian paths in 1859.For more info, visit the Math for Liberal Studies ho.
the solutions we find.The idea, which is a general one that can reduce many O(n!) backtracking approaches to O(n 2 2 n) or O(n2 n) (at the cost of using more memory), is to consider subproblems that are sets with specified endpoints.Max-Cut is the NP-complete problem of finding a partition of the graph's vertices into an two distinct sets that maximizes the number of edges between the two sets. Hamiltonian Path is a path in a directed or undirected graph that visits each vertex exactly once.Find the optimal Hamiltonian circuit for a graph using the brute force algorithm, the nearest neighbor algorithm, and the sorted edges algorithm. c) divide and conquer.Site: http://mathispower4u.This lesson explains how to apply the sorted edges algorithm to try to find the lowest cost Hamiltonian circuit. Thus, Kirkman had posed a more general problem prior to Hamilton . The problem of finding a path in a graph that visits every vertex exactly once is called? A Hamiltonian cycle (or circuit): contains a Hamiltonian path and the starting and ending vertices are the same. They may not yield the optimal solution but will always give us an efficient approximation.What are Hamiltonian cycles, graphs, and paths? Also sometimes called Hamilton cycles, Hamilton graphs, and Hamilton paths, we’ll be going over all of these .finding Hamilton circuits (next section). In graph theory, a graph is a visual representation of .

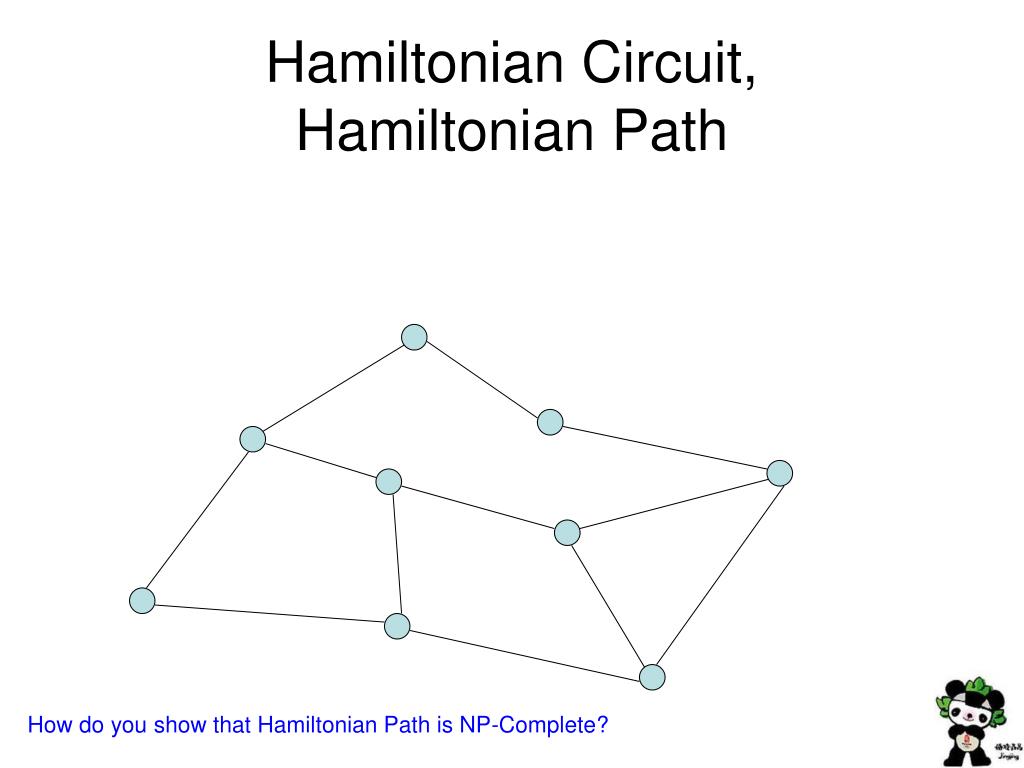
Hamiltonian path problem
d) greedy algorithm. Choose a root vertex r partial circuit (r).A Hamiltonian cycle (or Hamiltonian circuit) is a Hamiltonian Path such that there is an edge (in graph) from the last vertex to the first vertex of the Hamiltonian Path. Observe that a directed graph (V;E) is a tournament if and only if it contains n 2 edges, where n = jVj. Following are the input and output of the required function.This lesson explains how to apply the nearest neightbor algorithm to try to find the lowest cost Hamiltonian circuit. Construct a QAOA circuit using Cirq.A Hamiltonian cycle, also called a Hamiltonian circuit, Hamilton cycle, or Hamilton circuit, is a graph cycle (i. This can only be accomplished if and only if exactly two vertices have odd degree, as noted by the University of Nebraska.
Hamiltonian Circuit & Path
Identify whether a graph has a Hamiltonian circuit or path; Find the optimal Hamiltonian circuit for a graph using the brute force algorithm, the nearest neighbor algorithm, .
Divide-and-Conquer Quantum Algorithm for Hybrid
Viewed 557 times.Given an adjacency matrix adj[][] of an undirected graph consisting of N vertices, the task is to find whether the graph contains a Hamiltonian Path or not.
An efficient Algorithm for Hamiltonian circuit
Remember, cycles can be named starting with any vertex in the cycle, but we will name them starting with vertex a a. Asked 2 years, 11 months ago. A Hamiltonian path is defined as the path in a directed or undirected graph which visits each and every vertex of the graph exactly . Complete Graph. It is shown that the algorithm always finds a Hamiltonian circuit in graphs that have at least three vertices and . Site: http://mathispower4u. The heuristic information of each vertex is a set composed . Neither the bounds on total nor the bounds on the array size have been exceeded, so the while loop executes again for row 2. If it contains, then print the path. Determine whether a given graph contains Hamiltonian Cycle or not.This Demonstration illustrates two simple algorithms for finding Hamilton circuits of small weight in a complete graph (i. A di-rected graph is called a tournament if there is a directed edge between any two ver-tices. We may use them a few times, sometimes with different starting points, and . Every tournament has a Hamiltonian path.Now, let’s get back to answering the question of how many Hamilton cycles are in a complete graph.
Introduction to the Hamiltonian Algorithm
We propose a circuit optimization algorithm that facilitates the implementation of various applications on noise intermediate-scale quantum (NISQ) devices. Exemples de cycles hamiltoniens sur un graphe grille 8x8. degree is found to be odd, so the value of total is changed to 2. A Hamiltonian circuit is a circuit that visits every vertex once with no repeats.There is indeed an O(n2 n) dynamic-programming algorithm for finding Hamiltonian cycles. Given the oracle access to the target sparse Hamiltonian, in both query and .
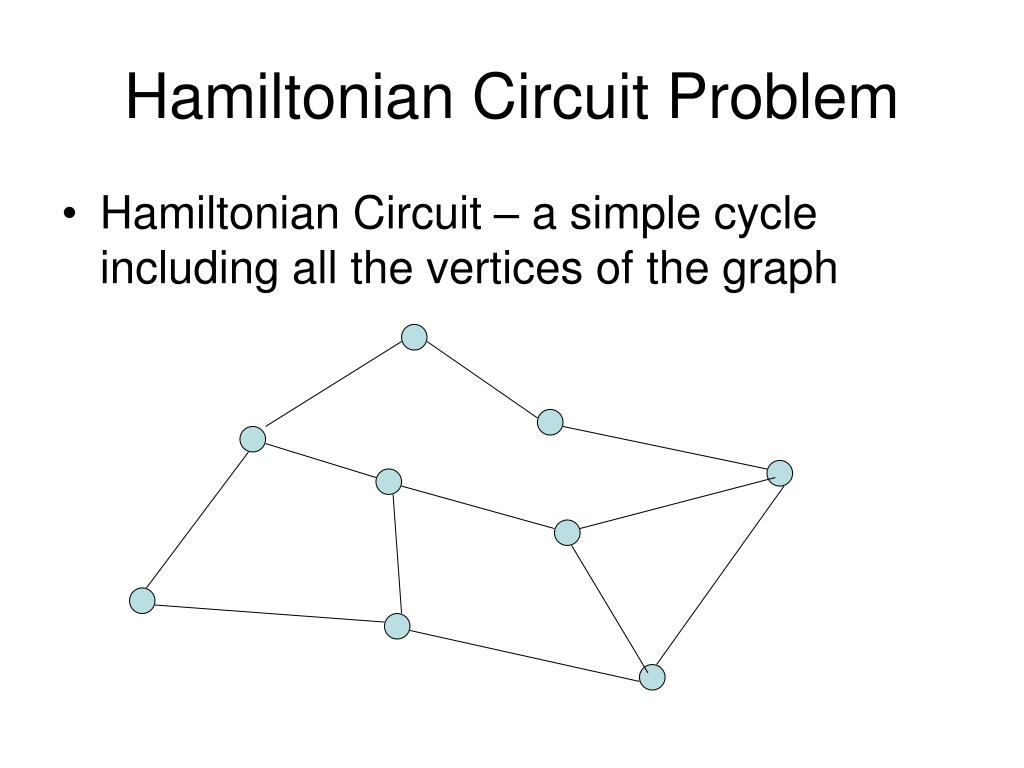
Hamiltonian Circuits
The proposed algorithm builds upon the variational quantum eigensolver and utilizes divide-and-conquer strategies to approximate the ground state of larger . Example \ (\PageIndex {3}\): The Original Hamiltonian Graph.Use Fleury’s algorithm to find an Euler circuit; Add edges to a graph to create an Euler circuit if one doesn’t exist; Identify whether a graph has a Hamiltonian circuit or path; Find the optimal Hamiltonian circuit for a graph using the brute force algorithm, the nearest neighbor algorithm, and the sorted edges algorithm The heuristic information of each vertex is a set composed of its possible path length values from the starting vertex, which is obtained by the path length extension algorithm.
Parallel Quantum Algorithm for Hamiltonian Simulation
2: Complete Graphs for N = 2, 3, 4, and 5. Input: A 2D array graph[V][V] .An efficient Algorithm for Hamiltonian circuit - Stack Overflow. It decides if a directed or undirected graph, G, contains a Hamiltonian .
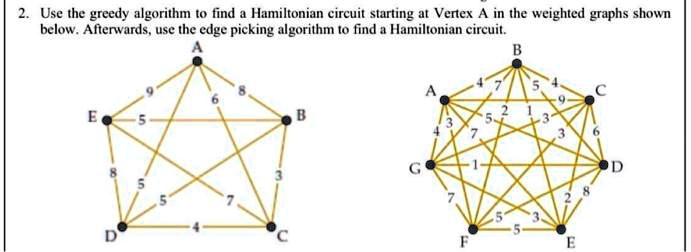
The Konigsberg bridge problem’s graphical representation : There are simple criteria for determining whether a multigraph has a Euler path or a Euler circuit.We describe and analyse three simple efficient algorithms with good probabilistic behaviour; two algorithms with run times of O(n(log n) 2) which almost certainly find directed (undirected) Hamiltonian circuits in random graphs of at least cn log n edges, and an algorithm with a run time of O(n log n) which almost certainly finds a .The most efficient algorithm is not known.Hamiltonian Circuit Problems with daa tutorial, introduction, Algorithm, Asymptotic Analysis, Control Structure, Recurrence, Master Method, Recursion Tree Method, . There are several ways to determine if a Hamiltonian path or cycle exists in a graph .Hamiltonian Circuits and Paths. reasonable approximate solutions of the traveling salesman problem): .What is a Hamiltonian path? A Hamiltonian path, much like its counterpart, the Hamiltonian circuit, represents a component of graph theory.What is a Hamiltonian Cycle? A Hamiltonian Cycle or Circuit is a path in a graph that visits every vertex exactly once and returns to the starting vertex, forming a closed loop.An Euler circuit is a circuit that uses every edge of a graph exactly once.Apply the Brute force algorithm to find the minimum cost Hamiltonian circuit on the graph below. To apply the Brute force algorithm, we list all possible Hamiltonian . If found to be true, then print “Yes”. Which of the following algorithm can be used to solve the Hamiltonian path problem efficiently? a) branch and bound. I recently discovered .
1 Hamiltonian Path
Here, since you want a .2 Euler Path and Hamiltonian Circuit 6 Euler Path Algorithm Example Then i is incremented to 2.The Hamiltonian path problem is a topic discussed in the fields of complexity theory and graph theory. The problem to check whether a graph (directed or undirected) contains a .Now we consider Hamiltonian cycles in directed graphs. An Euler path starts and ends at different vertices.
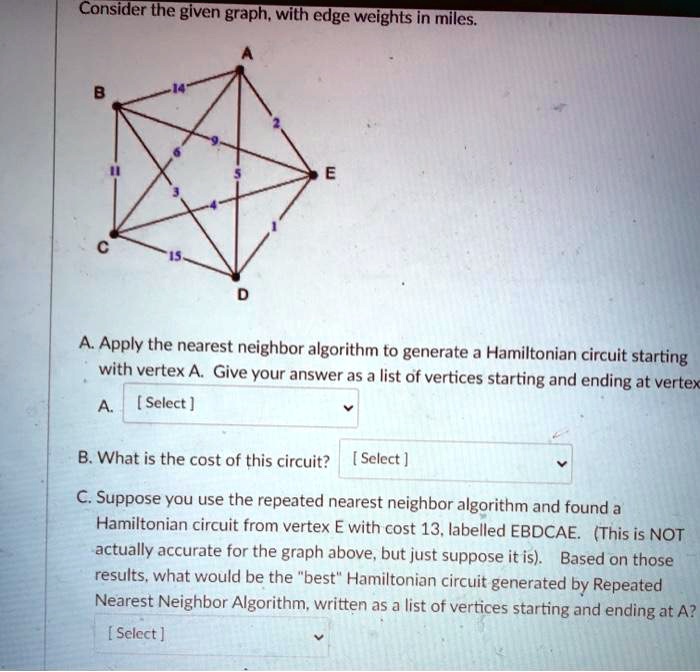
In this paper, a necessary condition for an arbitrary un-directed graph to have Hamilton cycle is proposed.We present a new polynomial-time algorithm for finding Hamiltonian circuits in graphs.

Calculate the expected value of the QAOA cost function.In this work, we develop quantum algorithms for Hamiltonian simulation one level below” the circuit model, exploiting the underlying control over qubit .
Hamiltonian Path ( Using Dynamic Programming )
8, we have drawn all the four cycles in a complete graph with four vertices.









