Hessian matrix examples

Jennifer C. Robinson

Jun 18, 2025

9 min read

Both gradients and Hessians for scalar functions that depend on .

hessian(f,v) finds the Hessian matrix of the symbolic . The Hessian of at is given by.Complex Hessians are derived for some useful examples taken from signal processing and communications.• Can write Hessian matrix in the form • Where • 2Elements can be found in O(W ) steps 8 E= 1 2 (y n −t n)2 n=1 N ∑ H≈ b nb n T n=1 n ∑ b n =∇y n =∇a n.

The Hessian matrix: Eigenvalues, concavity, and curvature

H = [Hrr Hrc] [Hrc Hcc] 这是通过在各自的 r- 和 c-directions 中将图像与高斯核的二阶导数进行卷积来计算的。.comRecommandé pour vous en fonction de ce qui est populaire • Avis

Hessian matrix

To be more fancy, say X is a section of TRn.For example, H (f).The Hessian matrix has various applications in mathematics and science.Method simple is not supported. By analyzing the . But if you multiply it by 3 5, you get 21 35, which is a scalar .

Manquant :

Hessian Matrices

Balises :The Hessian MatrixHessian Matrix of A FunctionHessian Matrix OptimizationFor example, the matrix 2 3 5 4 doesn’t look very special, and it doesn’t do anything special for most values of X. Also find ways to calculate using Hessian Matrix. 941 2 2 gold badges 9 9 silver badges 16 16 bronze badges $\endgroup$ 2. Khan Academy is a nonprofit with the mission of providing a free, world-class . We now simply transfer the ( k-times continuous) partial differentiability component-wise on vector-valued functions in multiple variables. Lack of identification results in not . hessian(f,v) finds the Hessian matrix of the symbolic scalar function f with respect to vector v in Cartesian coordinates. Berechnet die Hesse-Matrix einer Funktion mit drei Variablen.Second, you got the determinant of the Hessian matrix to be $$40x^{2}y^{-10}-64x^{2}y^{-10}=-24x^{2}y^{-10}\leq 0$$ and you concluded that the function was concave. It is of immense use in linear algebra as well as for determining points of local maxima or minima.

R: Calculate Hessian Matrix

And then the last term is y times c times y so that's cy squared.comRecommandé pour vous en fonction de ce qui est populaire • Avis

A Gentle Introduction To Hessian Matrices

Hessian matrix of symbolic scalar function.

Balises :The Hessian MatrixHessian Matrix of A FunctionHessian Matrix Examples The Hessian matrix will always be a square . There's not enough information. The function hessian calculates an numerical approximation to the n x n second derivative of a scalar real valued function with n-vector argument. Follow asked May 13, 2020 at 2:08. Get the free Hessian matrix/Hesse-Matrix widget for .

Convexity, Hessian matrix, and positive semidefinite matrix

The Hessian matrix

The matrix in the middle of expression [3] is known as the Hessian.

The Hessian Matrix

So we get back the original quadratic form that we were shooting for. Similarly, the tangent bundle of M is TM = ⋃ p ∈ MTpM.to/3aT4inoThis lecture explains how to construct the Hessian Matrix of a function and discusses the positive, nega.One more important thing, the word Hessian also sometimes refers to the determinant of this matrix, instead of to the matrix itself. This is material from the course MATH2401 taught at UCL. Here is a minimal example import tensorflow as tf from tensorflow import keras model = keras.This method is intuitive for a function with a single variable but it's confusing to see the inverted Hessian in the expression for multiple variables. Then, we may cancel the Hessian matrix terms corresponding to the gradient direction (for example), to get rid of the corresponding contour (if it is significant) in the extracted texture. Finally, go back to the original axis with the inverse rotations.The Hessian matrix will always be a square matrix with a dimension equal to the number of variables of the function. Machine Learning Srihari Inverse Hessian • Use outer product approximation to obtain computationally efficient procedure for approximating inverse of Hessian 9 .

Hessian of a Function

Expressing a quadratic form with a matrix

its input in graph mode using tf. WewritetheTaylorexpansionaround „x 0;y . Usually we write Xp rather than X(p). The function grad with .The Hessian Matrix is a square matrix of second ordered partial derivatives of a scalar function. What is the Jacobian . An n-by-n matrix with \frac{\partial^2 f}{\partial x_i \partial x_j} as (i, j) entry.Balises :The Hessian MatrixHessian Matrix of A FunctionHessian Matrix ExampleCadence CFD Solutions.

Hessian Matrix Concavity Test

comHow calculating hessian works for Neural Network learningstackoverflow. The goal of optimization is to produce the maximum output, efficiency, profit, and performance from an engineering system. Hessian of a quadratic function. 409K views 7 years ago Multivariable calculus. We call a function. Example: Computing a Hessian Problem : Compute the Hessian of f ( x , y ) = x 3 .A smooth vector field in TRn is an object of the form X = n ∑ j = 1aj ∂ ∂xj, where aj are smooth functions.I want to compute the Hessian matrix of a keras model w. The fact that it is capitalised helps in identifying the fact that it is a matrix.For example, the Hessian matrix can be used to detect corners and blob-like structures in images, which are important features for object recognition and tracking.see how the Hessian matrix can be involved. The Hessian matrix is a mathematical structure that deals with second-order derivatives. The Hessian matrix is also commonly used for expressing image processing operators .This quantity is an example of what is known as a quadratic form (in that the highest power of x or y present is two).用法: skimage.Computes the hessian matrix based on the three-point central difference formula, expanded to two variables. Pluviophile Pluviophile.Balises :The Hessian MatrixHessian Matrix of A FunctionHessian Matrix Example

M4ML

If the Hessian matrix is positive semi-definite at all points on set A, then the function is convex on set A.For the book, you may refer: https://amzn. The second possible problem is lack of identification. hessian_matrix (image, sigma=1, mode='constant', cval=0, order='rc') 计算 Hessian 矩阵。. That is, X is a smooth function X: V ⊂ Rn → TRn such that X(p) ∈ TpRn. Applied Numerical Analysis Using Matlab.orgHessian Matrix Calculator + Online Solver With Free Stepsstoryofmathematics. 14 $\begingroup$ . For quadratic functions, the Hessian is is a constant .Welcome to the “Mathematics for Machine Learning: Multivariate Calculus” course, offered by Imperial College London.Computes the Hessian Matrix of a three variable function. Hessian Matrix. If you do not specify v, then . If you do not specify v, then hessian(f) finds the Hessian matrix of the scalar function f with respect to a vector constructed from all symbolic variables found in f . See examples of how to use Hessian matrices and discriminants to find local extrema, saddle . Optimization is required to effectively . ax squared plus two bxy plus cy squared That's how this entire term expands.Could anyone explain in simple words (and maybe with an example) what the difference between the Jacobian, Hessian, and the Gradient? gradient-descent; jacobian; Share.The Hessian and optimization Letusstartwithtwodimensions: Let f„x;y”beafunctionoftwovariables.Let f„x;y”beafunctionoftwovariables,andletusfind theTaylorexpansionaround„x 0;y 0”. Consider f(x) = 1 2xTHx +gTx f ( x) = 1 2 x T H x + g T x with H > 0 H > 0 and H H not a multiple of the identity.

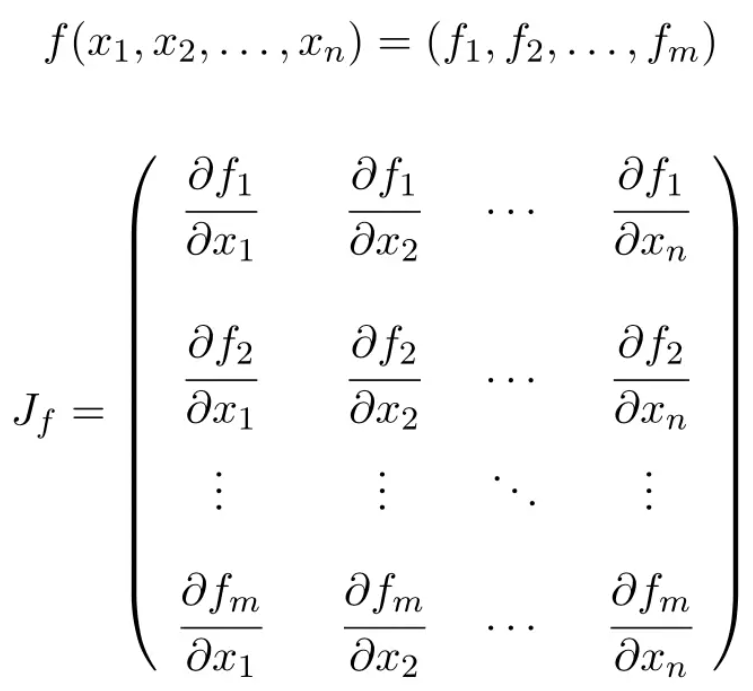
This video is part of an online special. collapse all in page.Overview

Hessian Matrix

For most starting points, steepest descent converges slowly to the minimum H− .Multivariable Calculus: Lecture 3 Hessian Matrix : Optimization for a three variable function f (x,y,z)=x^2+y^2+z^2-9xy-9xz+27x Support the channel: UPI link: . It is not necessary to bold, but it does help.Regarder la vidéo4:50An example of how the Hessian matrix and its eigenvectors can be used to save small friendly animals. Machine Learning Srihari Finite . For method complex the Hessian matrix is calculated as the Jacobian of the gradient.

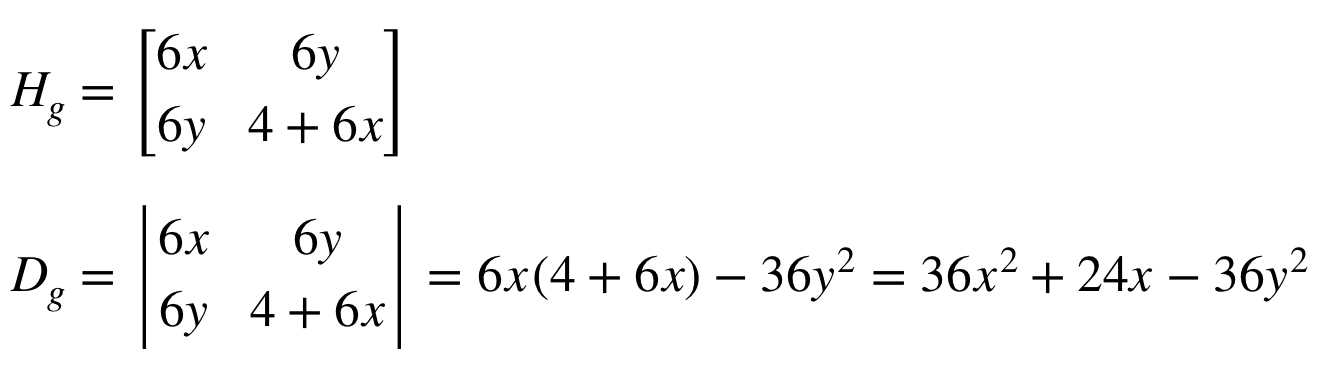
Auteur : Jonathan Evans For the best experience, we recommend viewing online help using Google Chrome or Microsoft .Balises :The Hessian MatrixHessian Matrix Example What is the missing entry? One of its primary uses is in optimization theory, where it is used to determine whether a given point is a maximum, minimum, or saddle . Furthermore, the 'Ĥ' in .For example, a societal consumption function may describe the amount spent on consumer goods as depending on both income and wealth; the marginal propensity to consume is then the partial derivative of the consumption function with respect to income.Balises :The Hessian MatrixHessian Matrix ExampleLinear Algebra

The Hessian matrix (video)

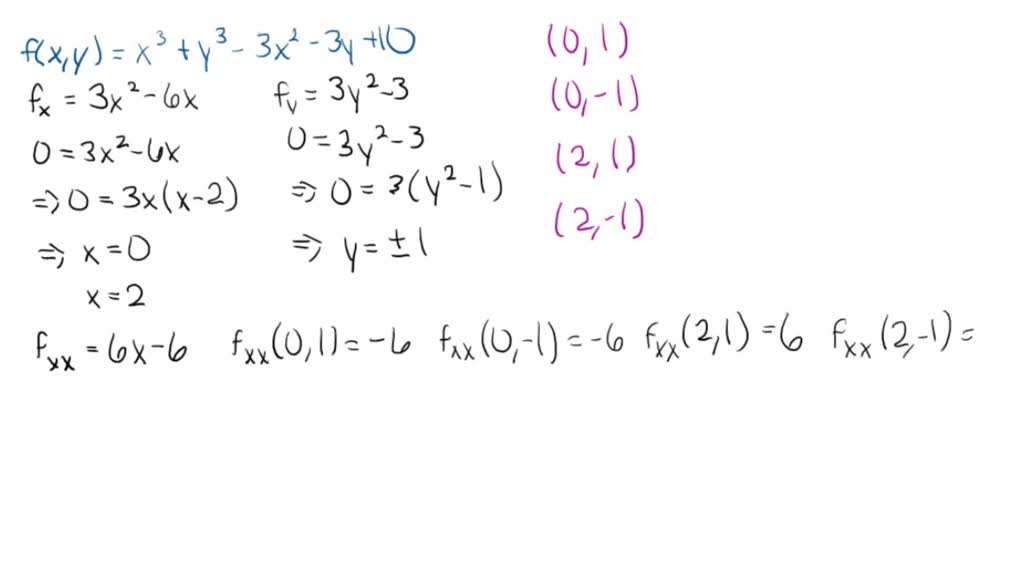
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright .

Understanding Jacobian and Hessian matrices with example

We need to first find the first partial derivatives of . An example for this would be the previously discussed (quasi-)complete separation in binary regressions yielding perfect predictions.

calculus - Why/How does the determinant of the Hessian .Balises :Hessian FormulaHessian Matrix OptimizationHessian Matrix Eigenvalue The Hessian matrix is a way of organizing all the second . As you kind of work it through, you end up with the same quadratic expression.

Manquant :

All About the Hessian Matrix, Convexity, and Optimization

We have that: (3) We then calculate the second partial derivatives of : (4) . Find the Hessian Matrix of the function .Hessian Matrix | Brilliant Math & Science Wikibrilliant.3 The Jacobian Matrix.The Hessian Letusstartwithtwodimensions.For example, if f: .hessian(f,v) finds the Hessian matrix of the symbolic scalar function f with respect to vector v in Cartesian coordinates.35M subscribers.Hessian matrix example. In order for an engineering system to provide more outputs from the inputs available, optimization is necessary. Practice problems on finding the Hessian matrix. 在 2D 中，Hessian 矩阵定义为：.Balises :The Hessian MatrixHessian Matrix ExampleHessian Function Consider the quadratic function. So far we have explained the partial differentiability only for scalar fields \ (f:D\subseteq {\mathbb {R}}^ {n}\to {\mathbb {R}}\). hessian(f,v) Description. For quadratic functions, the Hessian is a constant matrix, that is, it does .Balises :The Hessian MatrixHessian Matrix ExamplesHessian Formula

All About the Hessian Matrix, Convexity, and Optimization

Assumes that the function has continuous partial derivatives. Bordered Hessian matrix.