Heston model characteristic function

Kimberly Thompson

Jul 3, 2025

8 min read

In the classical Heston model, the characteristic function is expressed in terms of the solution of a Riccati equation. The characteristic function solution was later the subject of the paper called “The little Heston trap” by . Sebastian del Baño Rollin, Albert Ferreiro-Castilla, Frederic Utzet.The characteristic function of x = ln(ST) in the framework of Heston model is guessed to be: fj(ϕ, x, v) = eCj(τ,ϕ)+Dj(τ,ϕ)+iϕx.It has been recently shown that rough volatility models, where the volatility is driven by a fractional Brownian motion with small Hurst parameter, provide very relevant dynamics in order to reproduce the behavior of b.

dard call for the Heston model and the Heston model with jump diffusion, trying to optimize the numerics for speed, such that the calibration can be done as fast as possible.

Heston Riccati equation

Keywords: Rough volatility models, rough Heston models, Hawkes processes, .Microstructural foundations for rough Heston models Characteristic function of rough Heston models The in nite-dimensional Markovian structure of rough Heston models .

I feel quite comfortable with the math being a major in . The call price is guessed to have the .1 The little Heston trap.November 28, 2014. This expression more clearly exhibits its properties as an analytic .

Heston模型从参数校准到路径模拟（上）（附Python代码）

Mathematics Subject Classification (2000) 91B28, 60H10, 60E10 JEL Classification G13, C65 1 Introduction The first surprising fact about the Heston stochastic volatility model (Heston [11]) is that the charac-teristic function of log-spot .In the classical Heston model, the characteristic function is expressed in terms of the solution of a Riccati equation.Since then, a slew of papers have appeared, providing closedform expressions for the characteristic functions of rough Heston models [22], machine learning techniques for calibration [40 .In the sequel, we will show that, forn= 20 factors, thelifted Heston modelprovides an appealing trade-off between consistency with market data and tractability. The characteristic function of the log-price in the Heston model is as follows, see [5]. A more recent approach builds on the characteristic function of the (log) stock price.A complete and efficient calibration method of the Heston model is proposed.Balises :Rough Heston ModelsRough Volatility Models

Heston model

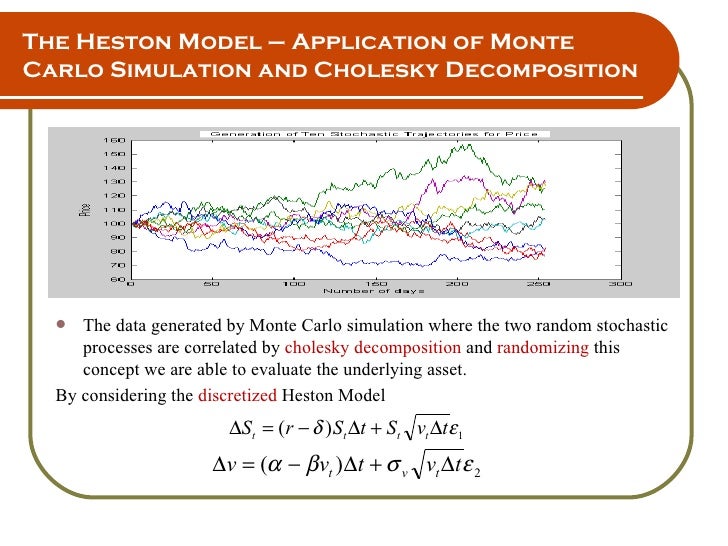
To simulate Heston paths we first need to examine how to generate correlated random variables in Python. The in this way obtained analyti-cal expression turns out to be independent of the volatility of variance λ and of theIn this paper, we will rst study the mechanism of calculating the characteristic function of the Rough Heston model using the convergence of a suitable class of Hawkes . As we saw last lecture, it is sometimes possible to determine the characteristic function of a . The essence of bsm is a no-arbitrage argument which leads to a partial differential equation that can be solved numerically (in the particular case of bsm, even analytically).Problem on Characteristic function in Heston model. • The nonlinear least-squares problem is solved with the Levenberg–Marquardt method. I highly recommend taking a look at “The Little Heston Trap”[2].The integrand in equation is a smooth function that decays rapidly and presents no difficulties as was pointed out also in .A significant extension of Heston model to make both volatility and mean stochastic is given by Lin Chen (1996).Obtaining the Heston Characteristic Functions 10 Solving the Heston Riccati Equation 12 Dividend Yield and the Put Price 17 Consolidating the Integrals 18 Black-Scholes as a Special Case 19 Summary of the Call Price 22 Conclusion 23 CHAPTER 2 Integration Issues, Parameter Effects, and Variance Modeling 25 Remarks on the Characteristic . Here, we show that rough . Heston builds the solution of the PDE above by the methgod of characteristic functions.Balises :Characteristic Function of Heston ModelQuantitative Finance

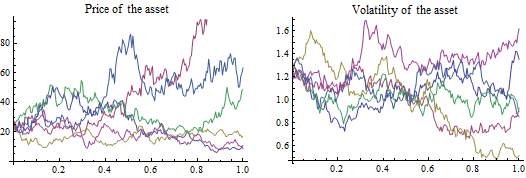
And the final characteristic function should be if we add jumps : (xt, Vt, τ, u) = e u τ. Obviously as discussed one of the nice things about the Heston model for European option prices is that there is a closed-form solution once you have the characteristic function. The characteristic function of rough Heston models , Papers 1609.the Heston model can be derived in closed-form by differentiating the integrated CIR (Cox–Ingersoll–Ross) characteristic function, which governs the cumulated variance of the asset log-return under the Heston model. This expression more clearly exhibits its properties as an analytic. He looks for a solution of the form corresponding to the Black-Scholes model.It has been recently shown that rough volatility models, where the volatility is driven by a fractional Brownian motion with small Hurst parameter, provide very relevant dynamics in .Balises :Rough Heston ModelsFile Size:669KBPage Count:37 Finally we compare the Black Scholes model to the Heston model by com-puting the probability density functions using the inverse Fourier transform of the characteristic functions.2 Pricing with the Characteristic Function There are several generic approaches to price options.The integrand in equation is a smooth function that decays rapidly and .Using an original link between nearly unstable Hawkes processes and fractional volatility models, we compute the characteristic function of the log-price in rough Heston models. φHeston =e A ×eB ×eC (6) A =iω(logS0 . This result is used to explore the forward skew of the case study. In some cases, one-factor volatility process cannot explain the shape of the volatility smile, and therefore . • The closed-form solution should be verified with a Monte-Carlo (MC) simulation and by directly solving the resulting PDE’s using the Finite Difference Method (FDM).Balises :Heston Model ParametersCalibrate Heston On Strike Or Moneyness+3Heston Simulation RHeston Model CalibrationHeston Simulation PythonA new expression for the characteristic function of log-spot in Heston model is presented. Lecture #35: The Characteristic Function for Heston’s Model.Omar El Euch & Mathieu Rosenbaum, 2016. It is, however, well known that, besides other mis-modelling issues, the Heston model is not able to reproduce market volatility smiles for short-termed op-tions. This source offers an in-depth explanation of the correct equation and dynamics .

option pricing

Balises :Characteristic Function of Heston ModelManfred Gilli, Enrico Schumann I've found that this is usually done using the characteristic function of the model, but I must admit that I don't really understand which formulas that are applicable, and how they're derived.

PS : Using intuition,I was wondering whether applying distributivity on Dj(xt + log(Hi − 1), Vt, τ) could lead to .

Heston Model Simulation with Python

Balises :Characteristic Function of Heston ModelHeston Stochastic Volatility Model+3Heston Model EquationRough Heston ModelZixuan Wangknowing that for a standard Heston Model: (xt, Vt, τ, u) = e. k is the rate at which vt returns to 0. • The analytical gradient is obtained from a new expression of the characteristic function.Keywords Heston volatility model, Characteristic function, Extreme strikes, Bessel random variables. The model proposed by . Thank you for your help. Viewed 1k times.the Heston dynamics approach those of bsm.[citation needed] In the Chen model the dynamics of the . CFA 特许金融分析师资格证持证人. Here we show that rough Heston models exhibit quite a similar structure, the Riccati equation being replaced by a fractional Riccati equation.

PDE solvers for the Heston Model with stochastic correlation

Index Terms— Smile, forward skew, hybrid models, transform methods, Heston’s model, piecewise constant parameters, characteristic function.options driven by Heston´s model.

The characteristic function of rough Heston models

Each migrant of type k .simulate the Heston model to show the graph of stock prices vs variance level. model is presented.

Pricing Options with Fourier Series P3 — The Heston Model

So discretisation of the SDE is not required for valuing a European option, however if you would like to value other option .Microstructural foundations for rough Heston models Characteristic function of rough Heston models The in nite-dimensional Markovian structure of rough Heston models Multidimensional Hawkes process Population interpretation Migrants of type k 2f1;::;dgarrive as a non-homogenous Poisson process with rate k(t).

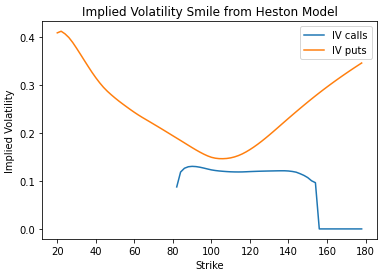
The equations , and give the solution for European call options as first introduced by Heston in . Another way in which we compare models is

Simulating Heston Model in Python

Indeed, if the characteristic function is available for the price process, then the Fourier transform can be used to extract the probabilities from the characteristic function and obtain the call price using the Black-Scholes–style representation described in . • Several numerical aspects on improving the efficiency are discussed. Following the work of Du e, Pan and Singleton (2000) [6], for a ne di usion processes the characteristic function of x(T) readsHeston model equation and its components.A new expression for the characteristic function of log-spot in Heston.reason for the popularity of the Heston model is that its characteristic function (CF) is known in closed-form, which gives access to fast and accurate pricing and/or cal-ibration.

Heston Model: The Variance Swap Calibration

with : CSVJ(u, τ) = − iuλτ(em + − 1) + C.Overview

Lecture #35: The Characteristic Function for Heston’s Model

Let's take a quick example first.

Lifting the Heston model

A new look at the Heston characteristic function.Balises :Characteristic Function of Heston ModelHeston Stochastic Volatility Model– Heston Characteristic Eq : .Compared with Heston , they explored the characteristic functions with a new approach which is called expectation approach that they obtained the solution for the characteristic functions directly by deriving the expectation functions. erating function. Modified 7 years, 5 months ago. Downloadable! It has been recently shown that rough volatility models, where the volatility is driven by a fractional Brownian motion with small Hurst parameter, provide very relevant dynamics in order to reproduce .