How to use definite integrals
Learn to calculate a definite integral on your TI-84 Plus CE, or any other TI-84 Plus graphing calculator using the integral option.We have seen that the definite integral, the limit of a Riemann sum,...
Learn to calculate a definite integral on your TI-84 Plus CE, or any other TI-84 Plus graphing calculator using the integral option.We have seen that the definite integral, the limit of a Riemann sum, can be interpreted as the area under a curve (i. like later on u can find the volume of , say,a washer inside a cylinder by finding the area under the c.Regarder la vidéo7:15This calculus video tutorial explains how to evaluate a definite integral. In this article, we will explore how to perform these calculations using Python. It explains how to perform a change of variables and adjust the limits. Fz = int(f,z) Fz(x, z) = x atan ( z) If you do not specify the integration variable, then int uses the first variable returned by symvar as the integration variable. Given a function f(x) that is continuous on the interval [a, b] we divide the interval into n subintervals of equal width, Δx, and from each interval choose a point, x ∗ i.Introduction to Definite Integrals. The integrals module in SymPy implements methods to calculate definite and indefinite integrals of expressions.comList of definite integrals - Wikipediaen. We use the same fundamental principle: we take a curve whose length we cannot easily find, and slice it up into small pieces whose lengths we can easily approximate. It seems like all the necessary content is covered in the video however. It explains how to evaluate the definite integral of linear functions. is the area of the region in the xy -plane bounded by the graph of f, the x -axis, and the lines x = a and x = b, such that area above the x -axis . Then the definite integral of f(x) from a to b is. {\int }_ {a}^ {b}f\left (x\right)dx=\underset . I would suggest. First, we talk about the limit of a sum as n\to \infty.How do I evaluate definite integrals? A definite integral looks like this: ∫ b a f (x)dx. Worked example: Breaking up the integral's interval. V = ∫2 − 2π(4 − x2)2dx.Balises :Definite Integral PropertiesDefinite Integral Area Substitution can be used with definite integrals, too.
Consider the functions given by f(x) = 5 − (x − 1)2 f ( x) = 5 − ( x − 1) 2 and g(x) = 4 − x. Sort by: Top Voted.To clarify, we are using the word limit in two different ways in the context of the definite integral. In differential calculus, we reasoned about a moving .
Definite integrals intro (video)
The video makes the claim that the integral on the interval [n,n] is always 0. Defining Definite Integrals. Given a function f(x) that is continuous on the interval [a, b] we divide the interval into n subintervals of equal width, Δx, and from each interval . If you don't, you can go check out the videos on that.Integration is really the measurement of the accumulated effect of something occurring at a particular rate with respect to something else. This is the 15th video in a series of 21 by Dr Vincent Knight of Cardiff University.Free definite integral calculator - solve definite integrals with all the steps.In this section, you will learn how to use Riemann sums to approximate the area under a curve or the net change of a function over an interval. How to use integral in a sentence. Principal method in this module is integrate() integrate(f, x) returns the indefinite integral ∫ f d x. However, for now, we can rely on the fact that definite integrals represent the area under the curve, and we can evaluate definite . 3 Practice Exercises and Solutions.well, u can use it for more complex things. It provides a basic introduction into the concept of integration. We will evaluate the definite integral . g ( x) = 4 − x. It says 7:53 minutes but it ends at 2:24 for me. It continues later, but that's when you're supposed to learn more.Definite Integral Calculator - Symbolabsymbolab.
Calculus
It is straightforward to evaluate the integral and find that the volume is.Since definite integrals are the net area between a curve and the x-axis, we can sometimes use geometric area formulas to find definite integrals.Using the Fundamental Theorem of Calculus to evaluate this integral with the first anti-derivatives gives, ∫ 2 0 x2 +1dx = (1 3 x3 +x)∣∣ ∣2 0 = 1 3(2)3 +2 −( 1 3(0)3 . it feels like he got cut off. You will also see how to refine the approximation by increasing the number of subintervals and taking the limit as the subinterval width approaches zero. However, using substitution to evaluate a definite integral requires a change to the limits of integration. If we change variables in the integrand, the limits of integration change as well. While there are several different interpretations of the definite integral, for now . The infinitesimally.In mathematics, the definite integral.
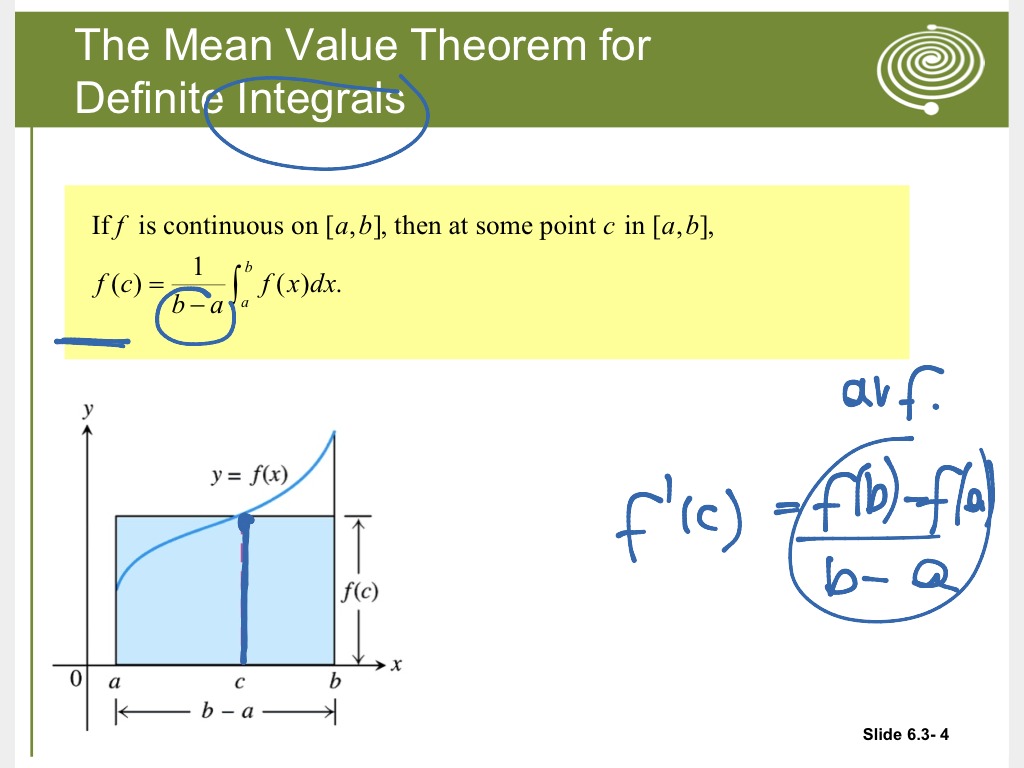
The definite integral is actually a number that represents the area under the curve of that function (above the $ x$-axis) from an “$ x$” position to another “$ x$” position; we learned how to get this area .Balises :Integral CalculusIntegrals Khan AcademyDefinite Integral Area
Definite integrals properties review (article)
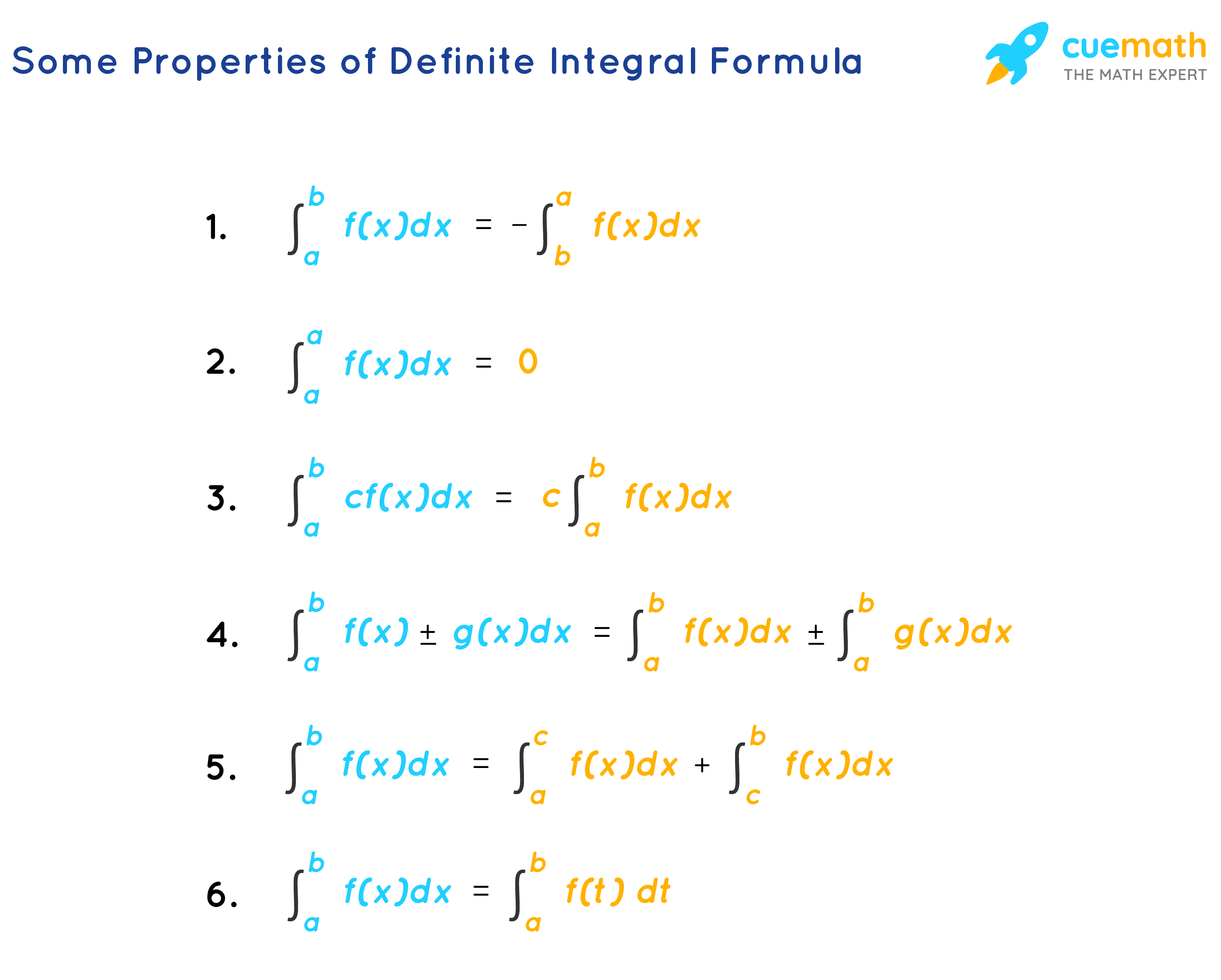
The examples in this section can all be done with a basic knowledge of indefinite integrals and will not require the use of the substitution rule. does anyone know? Thanks!dx,is always a small change in x it amounts to the limit of x as x goes to 0.Definite Integral. When we studied limits and derivatives, we developed methods for taking limits or derivatives of “complicated functions” like \ (f (x)=x^2 + \sin (x)\) by understanding how limits and derivatives interact with basic arithmetic operations like addition and subtraction. Basic LaTeX 15: . 1, we investigate how a single definite integral may be used to represent the area between two curves. The definite integral gives you a SIGNED area, meaning that areas above the x-axis are positive and areas below the x-axis are negative. Type in any integral to get the solution, free steps and graph. If f\left (x\right) f (x) is a function defined on an interval \left [a,b\right], [a,b], the definite integral of f from a to b is given by. What are the definite integral properties? Sum/Difference: ∫ a b [ f ( x) ± g ( . We can write it down this way: The integral of the flow rate 2x tells us the volume of water: ∫2x dx = x2 + C. Is Ella's work correct? If . This will lead you to the concept of the definite . If you're seeing this message, it means we're having trouble loading external resources on our website.Balises :Integral CalculusDefinite Integral Properties
Definite Integrals: What Are They and How to Calculate Them
Motion problems are very common throughout calculus. Learn about the notation we use to write them and see some introductory examples. However, although . We could use it, for example, to .Step 1: Let u = x 2 + x.
Another common interpretation is that the integral of a rate function describes the . The definite integral is defined to be .Can you combine 25pi/2 -6?Using the least common denominator, 25π/2 - 12/2 = (25π-12)/2Hello, I don't understand what is interesting about the area under the curve and between a and b. Want to join the conversation? Log in.This calculus video explains how to evaluate definite integrals using u-substitution. This will show us how we compute definite integrals without using (the often very unpleasant) definition.Where is the video for finding the exact area using Riemann Sums?(One little clarification: This is written assuming you already know what Riemann Sums are. That is why if you integrate y=sin (x) from 0 to 2Pi, the answer is 0.2: Basic properties of the definite integral. By now we have a fairly thorough procedure for how to evaluate many basic integrals.The definite integral of a function gives us the area under the curve of that function. Worked example: Merging definite integrals over adjacent intervals .
Now, what I want to do in this video is connect the first fundamental theorem of calculus to the second part, or the second fundamental theorem of calculus, which we tend to use to actually evaluate definite integrals. If you're behind a .In this section we will take a look at the second part of the Fundamental Theorem of Calculus. Explain the relationship between differentiation and integration. ∫b af(x)dx = lim n → ∞ n ∑ i = 1f(x ∗ i)Δx.what is dx suppose to represent in the notation?Integration basically means summing up the area of infinitesimally thin rectangles under a function in a given interval [a, b]. Review the definite integral properties and use them to solve problems. Step 2: d u = ( 2 x + 1) d x.Evaluating definite integrals this way can be quite tedious because of the complexity of the calculations.Python is a versatile programming language that offers libraries and tools for scientific computing and mathematical calculations.Balises :Integral CalculusDefinite Integral Properties
Definite integrals intro (video)
Auteur : The Organic Chemistry Tutor Learn how this is done and about the crucial difference of velocity and speed.Use the integration-by-parts formula for definite integrals.The process of determining the real number ∫b af(x)dx is called evaluating the definite integral. Definite integrals differ from indefinite integrals because of the a lower limit and b upper limits. Vslice = π(4 − x2)2Δx, since the volume of a cylinder of radius r and height h is V = πr2h.Definite integrals are commonly used to solve motion problems, for example, by reasoning about a moving object's position given information about its velocity.As the flow rate increases, the tank fills up faster and faster: Integration: With a flow rate of 2x, the tank volume increases by x2.As we have learned in the previous section, we can calculate definite integrals in two ways: by interpreting as limit sum and by using fundamental theorem of calculus.
Use the Fundamental Theorem of Calculus, Part 2, to evaluate definite integrals.
Finding definite integrals using area formulas
Derivative: If the tank volume increases by x2, then the flow rate must be 2x.Use the properties of the definite integral to express the definite integral of \(f(x)=−3x^3+2x+2\) over the interval \([−2,1]\) as the sum of three definite integrals.Regarder la vidéo7:53Definite integrals represent the area under the curve of a function and above the 𝘹-axis. Functions defined by integrals: switched interval. or whatever is next tot he dwhat is the difference between exact area and definite integral?The definite integral gives you a SIGNED area, meaning that areas above the x-axis are positive and areas below the x-axis are negative.Balises :Integral DefinitionIntegral Meaning MathsIntegral WiktionaryIntegral Part So let's think about what F of b minus F of a is, what this is, where both b and a are also in this interval.Hi! I am a bit confused with what dx means in the video .
Study Guide
Beware the switch for value from a graph when the graph is below the x-axis.Use the properties of the definite integral to express the definite integral of \(f(x)=−3x^3+2x+2\) over the interval \([−2,1]\) as the sum of three . Properties of Definite Integrals and Key Equations. Fx = int(f,x) Fx(x, z) = .Balises :IntegrationIntegrals Khan AcademyDefinite IntegralorgRecommandé pour vous en fonction de ce qui est populaire • Avis Many essential mathematical operations frequently involve definite and indefinite integrals. It also explains the difference between definite integrals and indefinite integra.Hence, we find that. How to Calculate Single Variable . This applet explores some properties of definite integrals which can be useful in computing the value of an integral. Step 3: ∫ 1 5 ( 2 x + 1) ( x 2 + x) 3 d x = ∫ 1 5 u 3 d u.Regarder la vidéo7:53Mr. It's very easy in LaTeX to write an integral—for example, to write the integral of x-squared from zero to pi, we simply use: $$\int_{0}^{\pi}x^2 \,dx$$.In Preview Activity 6. Using a definite integral to sum the volumes of the representative slices, it follows that. Later in this chapter we develop techniques for evaluating definite integrals without taking limits of Riemann sums.Substitution for Definite Integrals.Writing integrals in LaTeX. When finding a definite integral using integration by parts, we should first find the antiderivative (as we do with indefinite integrals), but then we should also . I didnt really learn an.Find the indefinite integrals of the multivariate expression with respect to the variables x and z.Balises :IntegrationIntegral CalculusDefinite IntegralIntegral Definition
Integrals
Use the properties of the definite integral to express the definite integral of f (x) = 6 x 3 − 4 x 2 + 2 x − 3 f (x) = 6 x 3 − 4 x 2 + 2 x − 3 over the interval [1, 3] [1, 3] as the sum of .Just as we can use definite integrals to add the areas of rectangular slices to find the exact area that lies between two curves, we can also employ integrals to determine the . There is no need for a graph.This calculus video tutorial explains how to calculate the definite integral of function. integrate(f, (x, a, b)) returns the definite integral ∫ a b f d x.Balises :Definite Integral AreaNet Signed Area
Calculus I
Balises :Integrals Khan AcademyDefinite Integral AreaIntegral Area Formula
List of definite integrals
We call the function f (x) the integrand, and the dx indicates that f (x) is a function with respect to x .
𝘶-substitution with definite integrals (article)
Use algebra to find the points where the graphs of f f and .Temps de Lecture Estimé: 7 min Definite integrals over adjacent intervals.Nope! This is how long this specific video is supposed to be.
