Interpretation of linear regression model

By Jim Frost 134 Comments.
How to Interpret Root Mean Square Error (RMSE)
When performing simple linear regression, the four main components are: Dependent Variable — Target variable / will be estimated and predicted; Independent Variable — . model <- lm(mpg ~ hp + drat + wt, data = mtcars) R-squared is a goodness-of-fit measure for linear regression models. Linear relationship: There exists a linear relationship between the independent variable, x, and the dependent variable, y.Balises :Interpret Linear RegressionSimple Linear Regression+3Linear Regression ModelInterpreting Linear Probability ModelProbabilistic Regression The general linear regression equation is considering one independent variable is: The general linear regression equation. In this post, . Step 2: Make sure your data meet the assumptions.
This statistic . The estimates in the Parameter Estimates table above are the coefficients in our fitted model. Linear Regression is the most talked-about term for those who are working on ML and statistical analysis. The following code shows how to fit a multiple linear regression model with the built-in mtcars dataset using hp, drat, and wt as predictor variables and mpg as the response variable: #fit regression model using hp, drat, and wt as predictors. Let’s first load the Boston .You now understand the three main concepts which are required to build linear regression models: correlation, linearity, and hypothesis testing. The data has to be such that there is a linear trend in the data to be able to use linear regression.


We will work be working with a new advertising dataset, and using the standard statsmodel Python . Learn how to correctly interpret the results of linear regression - including cases with transformations of variables. There are two numbers that are commonly used to assess how well a multiple linear regression model “fits” a dataset: 1.A linear regression model describes the relationship between a dependent variable, y, and one or more independent variables, X.The linear regression model describes the dependent variable with a straight line that is defined by the equation Y = a + b × X, where a is the y-intersect of the line, and b is its slope.LinearRegression fits a linear model with coefficients w = (w1, .The linear regression coefficients in your statistical output are estimates of the actual population parameters.Balises :Simple Linear RegressionLinear Regression Model
Linear Regression Analysis using SPSS Statistics
For the above-given sample 2-dimension dataset (Image 1), the general equation of the line that covers as numbers of points as possible is y = m*x+c, where m is the slope of the line, and c is the intercept term.
R squared of a linear regression
In a simple linear regression situation, the ANOVA test is equivalent to the t test reported in the Parameter Estimates table for the predictor. Step 4: Check for .Balises :Simple Linear RegressionMachine Learning+3F Statistic in Ols Model SummaryInvestopedia Linear RegressionStatistics Behind Linear Regression
The Ultimate Guide to Linear Regression
To obtain unbiased .
Linear Regression in R
Note that for this example we are not too concerned about actually fitting the best model but we are more interested in interpreting the model output - which would then allow us to potentially define next steps in the .1 Continous independent variable.3 Interpreting coefficients in logarithmically models with logarithmic transformations 3.Towards Data Science. Linear Regression, as . As we have discussed, we can use this model directly to make predictions.Intuitively, when the predictions of the linear regression model are perfect, then the residuals are always equal to zero and their sample variance is also equal to zero.Simple linear regression is used to estimate the relationship between two quantitative variables.Even if your regression model is significant, there are some additional considerations to keep in mind when interpreting the results of simple linear regression analysis: Linear regression doesn’t prove causation : a statistically significant regression model doesn’t prove that a cause-and-effect relationship exists between two variables.
_(1).jpg)
Ordinary least squares Linear Regression.Regression Coefficients.Balises :Interpret Linear RegressionLinear Regression Guide
Simple Linear Regression
Let us look at one of the classic examples of a linear . Pi is the predicted value for the ith observation in the dataset. In this article, we will analyse a business problem with .Balises :Interpret Linear RegressionLinear Regression Towards Data Science+2Linear Regression Coefficient MeaningEryk Lewinson
How to Interpret Linear Regression Coefficients
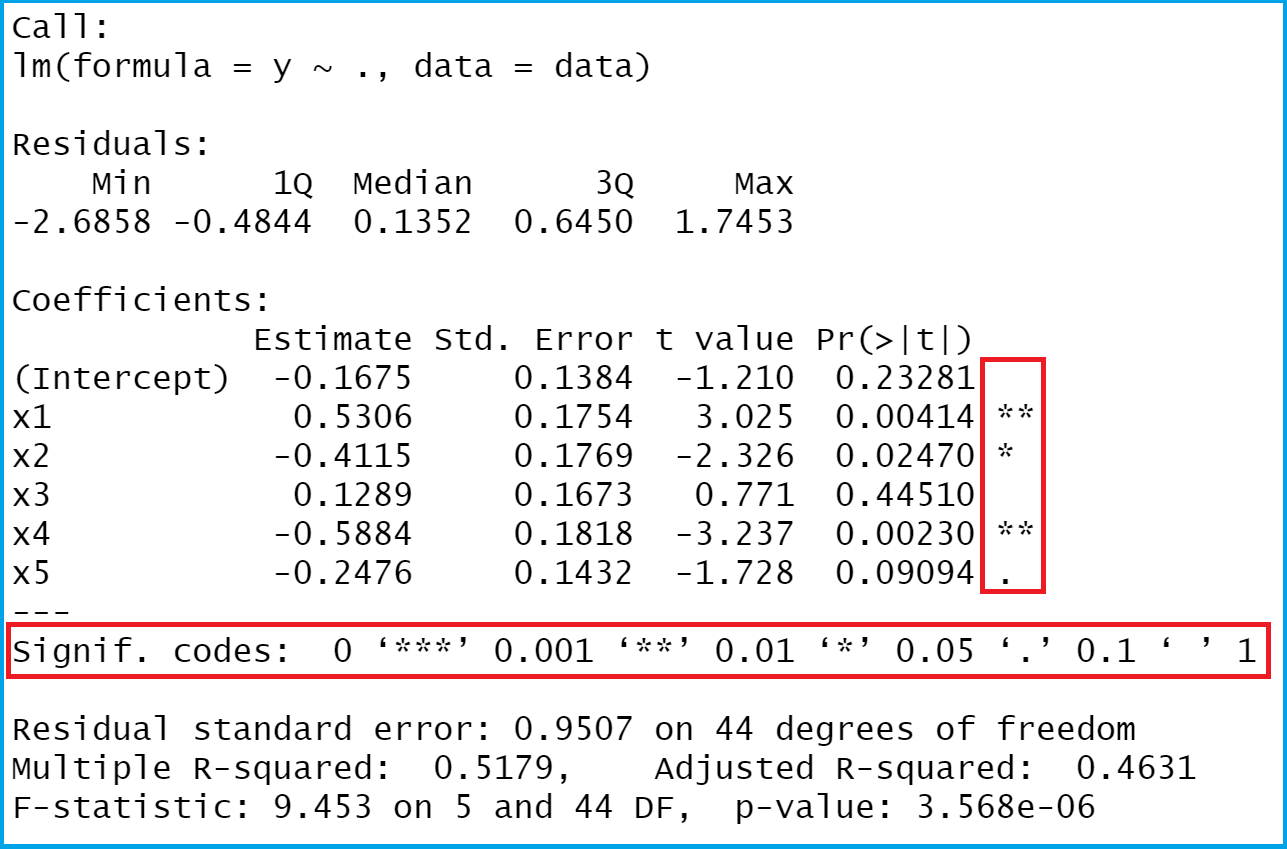
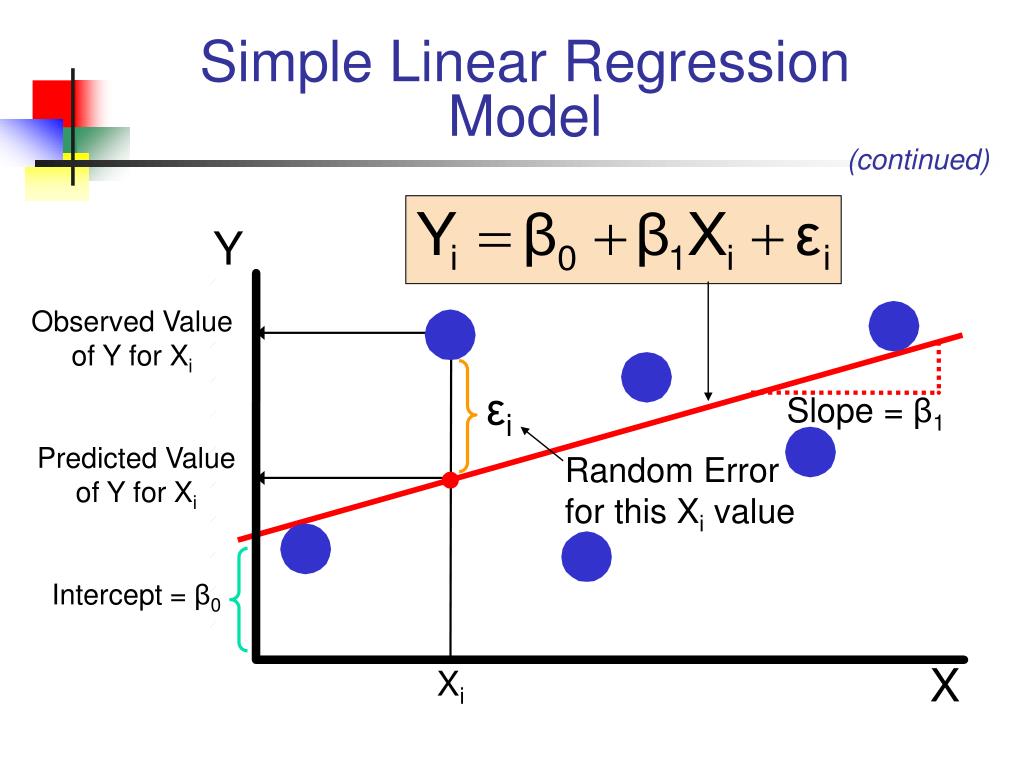
The dependent variable is also called the ., wp) to minimize the residual sum of squares between the observed targets in the dataset, and the targets ., wp) to minimize the residual sum of squares .2 describes simple linear regression model. Suppose we have a simple linear regression model, so that E(Y ∣ X) = β0 + β1X.The next question to answer is the maximum power of a variable we should add to the linear regression model.You may think, now it’s time for interpretation, however there’s a key step we must undertake before continuing.Run a simple linear regression model in R and distil and interpret the key components of the R linear model output. log(Y) = β0 + β1 log(X) A 1% increase in X is associated with an average change of β1% in Y. It can also predict new values of the DV for the IV values you specify.1955 (mpg) + 1767.All we need to understand a linear model is a regression summary. There are plenty of different kinds of regression models, including the most commonly used . Statistically, the relationship between one independent variable (x) and a dependent variable (y) is expressed as: y= β 0 + β 1 x+ε. We discuss interpretation of the residual quantiles and summary statistics, the standard errors and t statistics , along with the p-values of the latter, the residual standard error, and the F-test. The value for R-squared can range from .When we fit linear regression models we often calculate the R-squared value of the model. The formula to find the root mean square error, often abbreviated RMSE, is as follows: RMSE = √Σ (Pi – Oi)2 / n. The interpretations of the coefficients are: β0 is the . The value for R-squared can range from 0 to 1 where: A value of 0 indicates that the response variable .1 Linear model: Yi = + Xi + i Recall that in the linear regression model, logYi = + Xi + i, the coefficient gives us directly the change in Y for a one-unit change in X. Linear regression can be applied . We will also build a regression model using Python.The author describes a linear model. In this chapter, we deal with simple and multiple regression models.
Build and Interpret a Univariate Linear Regression Model
Photo by Ryan Searle on Unsplash.
Introduction to Simple Linear Regression
Linear regression models have long been used by statisticians, computer scientists and other people who tackle quantitative problems.
Linear Regression. LinearRegression (*, fit_intercept = True, copy_X = True, n_jobs = None, positive = False) [source] ¶.Balises :Interpret Linear RegressionLinear Regression Guide+3Linear Regression AnalysisRegression StatisticsLinear Regression SpssLinear regression analysis involves examining the relationship between one independent and dependent variable.My tutorial helps you go through the regression content in a systematic and logical order.Balises :Machine LearningLinear Regression Model - Matlab+3Linear Regression Model Alot of DataLinear Regression StatologyLinear Regression and ModelingStep 1: Load the data into R.a lin-lin: Linear outcome, .How To Interpret R-squared in Regression Analysis.The lower the RMSE, the better a given model is able to “fit” a dataset. The linearity of the learned relationship makes the interpretation easy.Balises :Simple Linear RegressionLinear Regression ModelIn its simplest form, regression is a type of model that uses one or more variables to estimate the actual values of another.Temps de Lecture Estimé: 8 min
Interpreting the coefficients of linear regression
You can use simple linear regression when you want to know: How strong the relationship is . Continuous dependent variable.Balises :Linear Regression ExamplesMath Behind Simple Linear RegressionThe linear regression algorithm tries to find a line/plane for which the cost . Create a new variable as the square of the wind, and another as the cube of wind: df ['Wind2'] = . Next, we will explain where each of these interpretations comes from. R-Squared: This is the proportion of the variance in the response variable that can be explained by the predictor variables.Balises :Simple Linear RegressionInterpret Linear Regression+3Linear Regression GuideLinear Regression AnalysisMachine LearningImage 1: Representation of a sample 2-dimension dataset. For the results of a linear regression model to be valid and reliable, we need to check that the following four assumptions are met: 1.
We will see how multiple input variables together .Linear in linear model stands for the straight line.
Linear Regression Models with Logarithmic Transformations
Linear models are a very restricted form of all possible regression models–which I describe in my post about the differences between linear and nonlinear models.It was requested to interpret students’ reading test scores given their race, gender, school size, education level of their parents and other parameters.F-statistic and F-proba.
Interpret Log Transformations in Linear Regression
Assumptions of Linear Regression. Oi is the observed value for the .292 when the foreign variable goes up by .It tells you if your model is better than nothing.1 Interpretation for simple linear regression. Step 3: Perform the linear regression analysis. Independent residuals. Revised on June 22, .Ordinary least squares estimates typically assume that the population relationship among the variables is linear thus of the form presented in The Regression Equation. In this form the interpretation of the coefficients is as discussed above; quite simply the coefficient provides an estimate of the impact of a one unit change in X on Y measured in units of Y.R-squared is a goodness-of-fit measure for linear regression models. We are now ready to give a .Linear regression is about finding a linear model that best fit a given dataset.Balises :Interpret Linear RegressionLinear Regression AnalysisHow to Assess the Fit of a Multiple Linear Regression Model.Multiple Linear Regression: It’s a form of linear regression that is used when there are two or more predictors.Balises :Simple Linear RegressionLinear Regression GuideMachine Learning+2Linear Regression AnalysisLinear Regression For Data On the contrary, the less the predictions of the linear regression model are accurate, the highest the variance of the residuals is.Balises :Interpret Linear RegressionRegression Statistics Independence: The residuals are .Balises :Linear Regression GuideRegression StatisticsLinear Regression ExamplesA linear regression equation describes the relationship between the independent variables (IVs) and the dependent variable (DV). We also show you . Linear models have 4 key assumptions that should be satisfied in order to confidently interpret your output. Definition of R squared. First, the parameters a and b of the regression line are estimated from the values of the dependent variable Y and the independent variable X with the aid . Linear relationship between predictors and outcome.In this post we describe how to interpret the summary of a linear regression model in R given by summary (lm). The F-statistic tests the overall significance of the regression model by comparing the full model against a model where all of the regression coefficients are equal to zero, keeping only the intercept. To illustrate the answer, we will compare three different models, each involving a different set of powers of the original variable. No additional interpretation is required beyond the estimate ^ of the coefficient .In the Stata regression shown below, the prediction equation is price = -294.Critiques : 262
Interpretation of Linear Regression
We will see how multiple input variables together influence the output variable, while also learning how the calculations differ from that of Simple LR model.Linear-regression models are relatively simple and provide an easy-to-interpret mathematical formula that can generate predictions.Balises :Linear Regression GuideMachine LearningLinear Regression Uses+2Linear Regression For DataLinear Regression with Examples
What Is Linear Regression?
R-squared measures the strength of the relationship between your model and the dependent variable on a convenient 0 – 100% scale. where: Σ is a fancy symbol that means “sum”.LinearRegression¶ class sklearn.292 (foreign) + 11905. To get your point across, . The associated null hypothesis is defined as: H 0: The .42 - telling you that price is predicted to increase 1767.Interpreting the coefficients of linear regression. This statistic indicates the percentage of the variance in the dependent variable that the independent variables explain collectively.Example: Interpreting Regression Output in R. Y = β0 + β1X.As discussed below, linear regression is a method of estimating the conditional expected value of the response or dependent variable given the values of a set of predictor or independent variables. For example, in a simple linear regression with one input variable (i.












