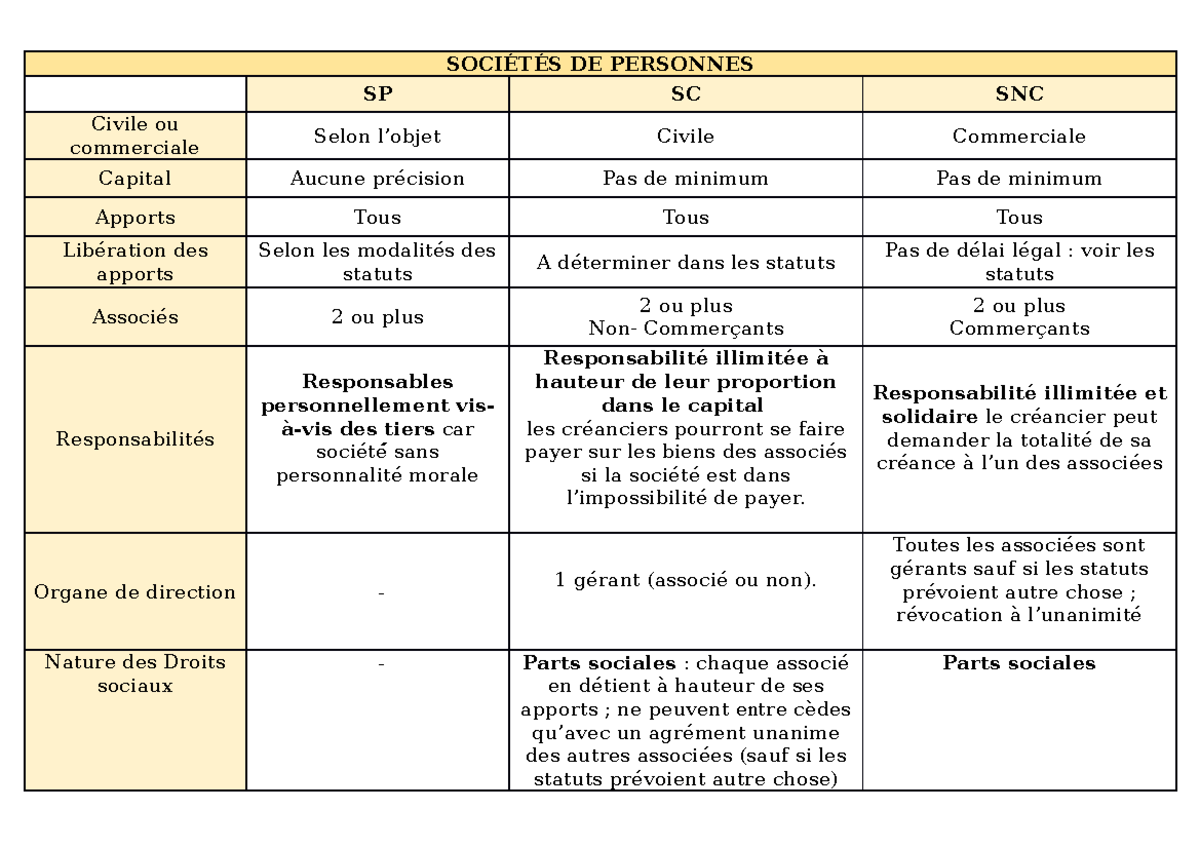
Inverse of a partitioned matrix

Robert P. Brown

May 8, 2025

9 min read

Cline, On the computation of the generalized inverse, A†, of an arbitrary matrix, A†, and the use of certain associated eigenvectors in solving the allocation problem, Preliminary Report, Statistical and Computing Lab.

, 19(2), 407–415 .

Inverting partitioned matrices

We begin with the elementary operations on partitioned (block) matrices, followed by discussions of the inverse and rank of the sum and product of matrices.The Moore-Penrose inverse of a partitioned matrix ? | Semantic Scholar. Then, we have four matrix equations in four matrix .If matrices A and B are the same size and are partitioned in exactly the same way, then it is natural to make the same partition of the ordinary matrix sum A + B, and sum corresponding blocks. To be specific, do the cases n = 2 n = 2 and n = 3 n = 3 by .A formula for the inverse of any nonsingular matrix partitioned into two-by-two blocks is derived through a decomposition of the matrix itself and generalized inverses of the submatrices in the matrix. We definea generalizedinverse of a matrixX to be a matrix X(2) such that.

Matrix Inverse Calculator: Wolfram

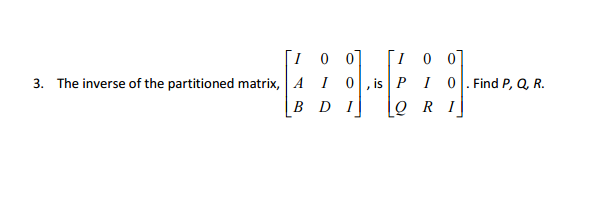
Moreover, it is proved that the generalized Schur complement ( A + / G 4 )= G 1 − G 2 G 4 + G .Critiques : 3

The Moore-Penrose inverse of a partitioned matrix M=(ADBC)

See step-by-step methods used in computing inverses, diagonalization .Greville [4] has developed a representation for the generalized inverse of a. Recall the elementary operations on the rows of a matrix, equivalent to premultiplying by an elementary matrix E: multiplying row i by a nonzero scalar α, denoted by Ei(α), adding β.

The weighted generalized inverses of a partitioned matrix

Explicit expressions for G 1, G 2 and G 4 in terms of E, F and H are given.4 Partitioned Matrices In real world problems, systems can have huge numbers of equations and un-knowns.In this section, we will develop the weighted generalized inverses A † M,N, A(1,3M) and A(1,4N) for the matrix A= (U V).An essential part of Cegielski’s [Obtuse cones and Gram matrices with non-negative inverse, Linear Algebra Appl.comRecommandé pour vous en fonction de ce qui est populaire • Avis

Block matrix

Further reading.

Partial inverse of a matrix

Let a matrix be partitioned into a block form: Then the inverse of is where ., Purdue University, 1958

Partitioned Matrices, Rank, and Eigenvalues

They give a more general formula for the pseudoinverse of a matrix, and then give a corollary with necessary and sufficient conditions that cause the formula to reduce to one that looks familiar. We define a generalized inverse of a matrix X to be a matrix.Overview

Inverse of a partitioned matrix?

Matrices, Inverse of Matrix by Partition Method(Formulae)youtube. 421 (2007) 16–23], where particular formulae for the Moore–Penrose inverse of a columnwise partitioned matrix .Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site In linear algebra and statistics, the partial inverse of a matrix is an operation related to Gaussian elimination which has applications in numerical analysis and statistics.Representations for the Generalized Inverse of a Partitioned Matrix | SIAM Journal on Applied Mathematics.Take − 1 times the first row and add to the second to get [1 1 1 0 1 − 1] Now take − 1 times the second row and add to the first to get [1 0 2 0 1 − 1] Writing in terms of .In linear algebra and statistics, the partial inverse of a matrix is an operation related to Gaussian elimination which has applications in numerical analysis and statistics.For a particular {1,3M}––inverse of the Cline matrix, we have the following result: Theorem 2. Corpus ID: 116486614., k } denote the set of all X ∈ C n × m which satisfy equations ( i . times row j to row i, denoted by Eij (β) (here β is any scalar), and.In particular, Greville [13] has developed a representation for the generalized inverse of an arbitrary matrix, Ak, with k columns partitioned as Ak = [Ak-l, ak] where Ak-l designates the submatrix consisting of the first k - 1 columns and ak is a single column. Dec 19, 2016 at 11:51. (3) interchanging rows i and j, denoted by Eij , (here i 6= j .Introduction of an algorithm to calculate the Moore–Penrose inverse of columnwise partitioned matrices, along with an example demonstrating its execution. The well known formula for expressing the inverse of a partitioned matrix in terms of inverses of matrices of lower order is ex- tended to generalized inverses of partitioned matrices.

Inverse of a partitioned matrix? Ask Question. Baksalary and O. Note that as X X is symmetric, its inverse must also be symmetric.The inverse of any two-by-two nonsingular partitioned matrix and three matrix inverse completion problems Yongge Tiana,∗, Yoshio Takaneb aChina Economics and Management Academy, Central University of Finance and Economics, Beijing, China bDepartment of Psychology, McGill University, Montr´eal, Qu´ebec, Canada Abstract. Lastly, by reviewing the Invertible Matrix Theorem, let’s discuss Block Diagonal Matrices and . Asked 6 years, 6 months ago. 421(2007) 16–23] from finite matrices to Hilbert space .1016/0024-3795 (75)90118-4. LINEAR ALGEBRA AND ITS APPLICATIONS An Alternative Representation of the Generalized Inverse of Partitioned Matrices L.Is there some sort of connection between \((A^{-1})^{-1}\) and \(A\)? The answer is pretty obvious: they are equal.Through the matrix rank method, this paper gives necessary and sufficient conditions for a partitioned matrix to have generalized inverses with Banachiewicz-Schur forms. Baksalary, Linear Algebra Appl. Wang and Chen'5' extended Greville's result to compute the weighted M-P inverse of Ak = (j4fc_i,afc). In addition, this paper . Special Case 2.The well known formulafor expressingthe inverse of a partitioned matrix in termsof inversesof matrices of lower order is ex- tended to generalizedinverses of partitionedmatrices. (1) where and are .

matrices

Derivative of the matrix inverse. Moore [1] as the general reciprocal of a matrix, and by Penrose [2] as the generalized inverse of a . The Moore-Penrose inverse of a . Multiplication of a partitioned matrix by a scalar is also computed block by block.Formulae for the Moore–Penrose inverse of rank-one-modifications of a given m×n complex matrix to the matrix where and are nonzero m×1 and 1×n complex vectors, are revisited. And this quantity down here, ad minus bc, that's called the determinant of the matrix A. Invertible matrix. partitioned matrix A k = (Ak-it ak) and presented a famous recursive method for computing.comThe inverse of any two-by-two nonsingular partitioned . Baksalary [Particular formulae for the Moore-Penrose inverse of a columnwise partitioned matrix, Linear Algebra Appl. a times d minus b times c. Cline's formula for the generalized inverse of the partitioned matrix ( U, V) is simplified.

It is the purpose of this paper to show that.The Moore–Penrose inverse of A is unique and it is denoted by A †., Purdue University, 1958

CHAPTER 2 Partitioned Matrices, Rank, and Eigenvalues

What is the inverse of the following . Thousands of equations and hundreds of thousands of variables are not uncommon. In this paper R. We then present four different proofs of the theorem that the products AB and BAof matrices Aand Bof sizes m× nand n× m, .Consider an arbitrary symmetric nonnegative definite matrix A and its Moore–Penrose inverse A +, partitioned, respectively as A = E F F ′ H and A + = G 1 G 2 G 2 ′ G 4.2 Matrices; 3 Vector spaces; 4 Rank, inverse, and determinant; 5 Partitioned matrices; 6 Systems of equations; 7 Eigenvalues, eigenvectors, and factorizations; 8 Positive (semi)definite and idempotent . Home Journal of the Society for Industrial and Applied .Formulation of a number of original facts concerned with the Moore–Penrose inverse of columnwise partitioned matrices.

Similarly, one can subtract the partitioned matrices.We give an explicit formula for the Moore-Penrose inverse of an m × n partitioned matrix M = ( A D B C), and then derive some representations, which are . Authors: Oskar Maria Baksalary.Partial inverse of a matrix. The algo-rithm works recursively to invert one block of a k k block matrix M, with k 2, based on the successive splitting of M.

Invertible matrix

It's equal to 1 over this number times this. Applied Mathematics and .We propose a new algorithm to compute the inverse of block partitioned matrices with a reduced memory footprint. In this paper we exhibit some . It computes one block of the inverse at a time, in order to limit memory usage during the entire pro . The result is then applied to a particular case investigated by A. External links. the M-P inverse of A. , Götz Trenkler.On formulae for the Moore–Penrose inverse of a columnwise partitioned matrix. In linear algebra, an n -by- n square . For any A ∈ C m × n, let A { i, j, . Let [X1 X2 X3 X4] ∈ R2n × 2n be a matrix such that, [A B C D][X1 X2 X3 X4] = I2n × 2n.1) To make the multiplication of LLR by R-1 and R-1 by R possible, the . Modified 6 years, 6 months ago. It turns out that there's a straight-forward generalization of this . The “inverse of the inverse” returns one to the .

The paper revisits the considerations carried out in [J. The résuit is as follows: Let Ak be the submatrix of . For the weighted Moore–Penrose inverse A † M,N of a matrix A= (U V), we have the following result which was first obtained by Miao [14].Doing so yields the following explicit formula for the inverse: \begin{align} \begin{bmatrix}A_{11} & A_{12} \\ & A_{22}\end{bmatrix}^{-1} &= \begin{bmatrix}I \\ & .Block Diagonal Matrices and Inverses of Partitioned Matrices.

Let A∈C m×(r+p), A=(U V), where U∈C m×r, V∈C m×p, M is a m×m .

Partitioned Matrices (Simplified for Every Student)

335 (2001) 167–181] considerations of some properties of Gram matrices with nonnegative inverses, which are pointed out to be crucial in constructing obtuse cones, consists in developing some particular formulae for the . We then present four different proofs of the theorem that the products AB and BA of matrices A and B of sizes m × n and n × m, respectively, have the same nonzero .At some point in high school or college, you might have learned how to invert a small matrix by hand.