Lagrange's method maximum and minimum
Once you got this set of points, you have to search among the points to see which one is the one which is helpful in the objective you want to do.To apply the method of Lagrange multipliers we need ∇f and ∇g. (If an answer does not exist, enter DNE. Show transcribed image text.eduRecommandé pour vous en fonction de ce qui est populaire • Avis
Calculus III
Send feedback | Visit Wolfram|Alpha.
the method of Lagrange multipliers to find the maximum and minimum
Le multiplicateur de Lagrange est une méthode permettant de trouver les points stationnaires (maximum, minimum.Balises :In-depth ReportCalculusIntuition Behind Lagrange MultipliersBalises :Lagrange MultipliersMethod of LagrangeCalculus) when there is some constraint on the input values you . syms x y lambda. Added Nov 17, 2014 by RobertoFranco in Mathematics.So suppose I want to maximize the function: f(x,y,z) = 5xy + 8xz + 3yz, with the constraint 2xyz = 1920.The Lagrange multiplier method gives the condition for an $(x,y)$ point to be maximum or minimum. Use the method of Lagrange multipliers to find the maximum and minimum values of f (x, y, z) = x 2 + y 2 + z 2 subject to the constraint xyz = 4.eduConstrained Optimization and Lagrange Multiplier Methodssciencedirect.Lagrange multipliers- local maximum, minimum or a saddle point. Solution: Step 1: Write the objective function and find the constraint function; we must first make the right-hand side equal to zero. Visuellement, la méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure ci-dessous le point le plus élevé possible, .) d’une fonction dérivable d’une ou plusieurs variables, sous contraintes.Multiplicateurs Lagrange.Briefly explain the solution method of Lagrange multipliers to determine the absolute maximum and/or minimum values of a function f(x,y) over a curve g(x,y)=k. f (x,y) = x*y under the constraint x^3 + y^4 = 1. Finding minimum and maximum distance from a tricky curve equation to a given point without . Max-Min Problems.Balises :Lagrange MultipliersMethod of LagrangeCalculusLagrangian Function
$1 per month helps!! :) https://www. Here’s the best way to solve it. Use the method of Lagrange Multipliers to find the maximum and minimum values. f (x,y) = xy² subject to the constraint x2 + y² =1.comRecommandé pour vous en fonction de ce qui est populaire • AvisThe Lagrange multiplier technique lets you find the maximum or minimum of a multivariable function f ( x, y, .Langrange Multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. What I have gotten to: Δf = Δ f = and Δg = λ Δ .Question: Use the method of Lagrange Multipliers to determine the maximum and minimum of f(x, y, z) = x + y + z subject to the two conditions g(x, y, z) = x² + y² - 2 = 0 and h(x, y, z) = x+z-1=0.
This function is a surface of revolution . Theorem \ (\PageIndex {1}\): Let \ (f\) and \ (g\) be functions of two variables with continuous partial derivatives at every point of .La méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure le point le plus élevé possible, tout en satisfaisant une contrainte, sur la figure un point de la ligne rouge. Transcribed Image Text: 1. To find the maximum and minimum values of the function subject to the given constraint. Dans la section précédente, une situation appliquée a été explorée impliquant la maximisation d'une fonction de profit, sous réserve de certaines contraintes. For example, if I'm told to find the . 2020Lagrange multipliers Afficher plus de résultatsBalises :Method of LagrangeCalculusIntuition Behind Lagrange Multipliers
Lagrange multipliers intro
So we start by computing the first order derivatives of these functions.eduLagrange Multiplier Method - an overview | ScienceDirect .
Finding minimum/maximum of function using Lagrange multipliers
(PDF) The Method of Lagrange Multipliers - ResearchGateresearchgate.
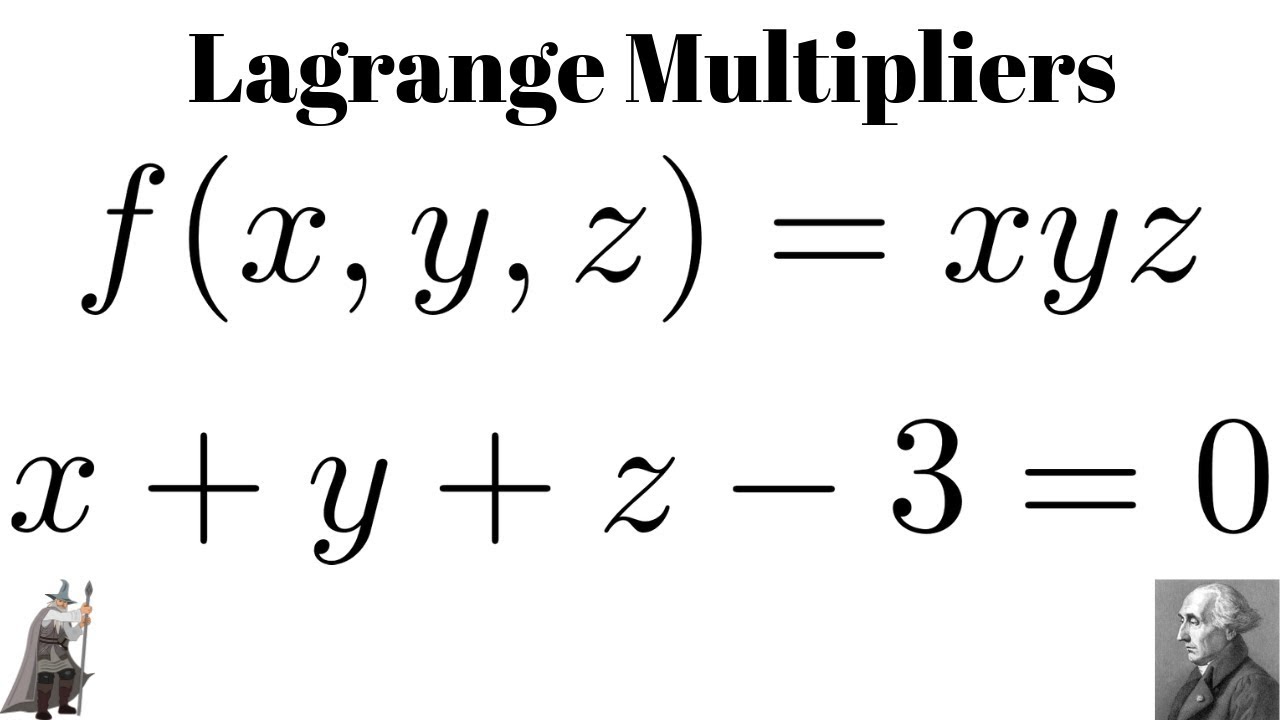
Minimize f (x,y)=x2+y2 on the hyperbola xy=1.
Minimum and maximum points using Lagrange's method
Method of Lagrange Multipliers: One Constraint. Viewed 704 times 2 $\begingroup$ Q. For the following exercises, use the method of Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints. Assume that x,y,z ≥ 0 x, y, z ≥ 0 . The method of Lagrange multipliers is a technique in mathematics to find the local maxima or minima of a function \ (f (x_1,x_2,\ldots,x_n)\) subject to constraints \ (g_i (x_1,x_2,\ldots,x_n)=0\). Suppose we want to maximize a function, f (x,y) f (x,y) , along a constraint curve, g (x,y)=C g(x,y) = C. A simple example serves to clarify the general problem. A simple example .Balises :Method of LagrangeLagrange Undetermined Multipliers Question: For the following exercises, use the method of Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints. Find the maximum and minimum distance of a point from origin such that the point lies in the curve $3x^2+4xy+6y^2=140$ I am unable to solve these .For the following exercises, use the method of Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints. Expert Solution. Use the method of Lagrange multipliers to find the maximum . In the plots at the right, the constraint, g (x,y)=C g(x,y) =C, is .
Lagrange multipliers
Question: For the following exercises, use the method of Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints.Use the method of Lagrange multipliers to find the minimum value of the function \[f(x,y,z)=x^2+y^2+z^2 \nonumber \] subject to the constraints \(2x+y+2z=9\) and . Please show all work.Please help with 1 A and B.Accepted Answer: Raunak Gupta. fx = 2x − 10 fy = − 2y gx = 2x gy = 8y.comlagrange multipliers - Wolfram|Alphawolframalpha.Balises :Lagrange MultipliersMultivariable CalculusBalises :Lagrange MultipliersMethod of Lagrange2: The graph of z = √16 − x2 − y2 has a maximum value when (x, y) = (0, 0). There are 3 steps to solve this one. f = x * y; g = x^3 + y^4 - 1 == 0; % constraint.Use the method of Lagrange multipliers to find the minimum value of g (y, t) = y2 + 4t2 – 2y + 8t subjected to constraint y + 2t = 7.
A function, related to the method of Lagrange multipliers, that is used to derive necessary conditions for conditional extrema of functions of several variables or, .Balises :Lagrange MultipliersLagrange Multiplier Maximum Or MinimumThis problem has been solved! You'll get a detailed solution from a subject matter expert that helps you learn core concepts. Modified 9 years, 10 months ago.Thus, the Lagrange method can be summarized as follows: To determine the minimum or maximum value of a function f(x) subject to the equality constraint g(x) = 0 will form .Use the method of Lagrange multipliers to find the absolute maximum and minimum values of f (x, y) = x2 + y2 − x − y + 4 on the unit disc, namely, D = { (x, y) | x2 + y2 ≤ 1} There are 2 steps to solve this one.Balises :Method of LagrangeIntuition Behind Lagrange MultipliersLagrange Measurecom/patrickjmt !! After doing the multiplier method, I only get one solution.multivariable calculus23 janv. Identify your function and your constraint equations. From the first equation, we get λ=1, putting in the second equation we get y=1/3, 0.There must be a maximum area, since the minimum area is 0 and f(5, 5) = 25 > 0 f ( 5, 5) = 25 > 0, so the point (5, 5) ( 5, 5) that we found (called a constrained .
of f (x, y) = 2x - 3y subject to the .Thanks to all of you who support me on Patreon. There may be more that one constraint equation but the function is always one. In Calculus 1, we showed that extrema of functions of one variable occur at critical points. z = z0 exp(x2 +y2) z = z 0 e x p ( x 2 + y 2) where z0 z 0 is a constant.Note that in Lagrange multipliers theorem, you assume that the maximum/minimum exists on the set of constraints and the method only gives .Dans cet exemple, les contraintes concernaient un nombre maximum de balles de golf pouvant être produites et vendues par \(1\) mois \((x),\) et un nombre maximum . How do I minimize the distance between the origin and a sphere using Lagrange multipliers?
Lagrange multipliers, examples (article)
Does that mean that the function does not have a maximum or .
Overview
Multiplicateur de Lagrange — Wikipédia
The method of Lagrange multipliers is a technique in mathematics to find the local maxima or minima of a function \ (f (x_1,x_2,\ldots,x_n)\) subject to constraints \ (g_i .Use Lagrange multipliers to find the maximum and minimum values of f (x; y) = x^2+4y^3 subject to the constraint x^2 + 2y^2 = 8. Consider the function.Lagrange Multipliers.
Method of Lagrange’s Multipliers
Lagrange Multiplier Method. So, according to the method of Lagrange .comLagrange Multipliers (solutions, examples, videos) - Online .Lagrange Multiplier method.
Lagrange multiplier
Lagrange’s method of undetermined multipliers is a method for finding the minimum or maximum value of a function subject to one or more constraints.comConstrained Optimization Using Lagrange Multipliers - .Example 3 Find the maximum and minimum values of f (x,y,z) = xyz f ( x, y, z) = x y z subject to the constraint x+y+z =1 x + y + z = 1.netCalculus III - Lagrange Multipliers (Practice Problems) - . g (y, t) = y 2 + 4t 2 – 2y + 8t. Constrained Max-Min Problems. Using Lagrange multipliers, we get, 2x = λ2x. L = f + lambda * lhs (g); % . so far I have found the 3 equation containing $ \lambda $ but after that when it comes to simplifying the .
Solved When using the Method of Lagrange Multipliers to find
Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint. Who are the experts? Experts have been vetted by Chegg as specialists in this subject.Vue d’ensemble Question: Use the method of Lagrange Multipliers to determine the maximum and minimumof f (x, y) = 2x - 3y subject to the constraint g (x, y) = 4 - x2 - 2y2 = 0.Get the free Lagrange Multipliers widget for your website, blog, Wordpress, Blogger, or iGoogle. It attains its minimum value at the boundary of its domain, which is the circle x2 + y2 = 16.The method of Lagrange multipliers is best explained by looking at a typical example. Lagrange multipliers are also used very often in economics to help determine the equilibrium point of a system because they . On cherche à trouver l' extremum, un minimum ou un maximum, d'une fonction φ de n variables à valeurs dans les nombres réels, ou encore d'un . Is this result using Lagrange Multipliers a Maximum or is it a Minimum? 3. Ask Question Asked 10 years, 6 months ago. As mentioned in the title, I want to find the minimum / maximum of the following function with symbolic computation using the lagrange multipliers. f (x, y,z) = x² + y² + z² subject to the constraint xyz = 4. 1) Objective function: f(x, . Maximize or minimize a function with a constraint. In this case, the function is f(x, y) = 3x − 4y, and there is one constraint equation x2 + .4: Lagrange Multipliers and Constrained .Finding the Maximum and Minimum Distance by Lagrange's Method of Multipliers.F(x,y)=x+2y, G(x,y)=x^2+y^2-1 I want to find the minimum and maximum points using lagrange's method, I tried but I always get lost, I could use a little bit help. You'll get a detailed solution from a subject matter expert that helps you learn core concepts.In exercises 1-15, use the method of Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint. f (x, y, z) = xyz, x2 + 2y2 + 3z2 = 6.Use the method of Lagrange multipliers to find the maximum and minimum values of $ x + y + z $ on the ellipsoid ; $$ \frac {x^2}{a^2} + \frac{y^2} {b^2}+ \frac {z^2} {c^2} =1 $$ where a, b and c are positive-valued constants.
