Local stability vs global stability

Ashley

May 20, 2025

10 min read

global stability analysis performed using the same wall geometry and matrix soil properties as provided in Figure 4. Asked 10 years, 3 months ago.

Under certain analytic and geometric assumptions we show that local stability of the coexistence (positive) fixed point of the planar Ricker competition model implies global stability with respect to the interior of the positive quadrant. We give several sufficient conditions for global stability, and use these conditions to show that for the usual population models from the litterature, local and global stability do coincide.Local and global aspects of almost global stability Pablo Monzon and Rafael Potrie´ Abstract—In this work we introduce several known and new results on almost global stability. 1, Amel Hioual. Quantifying the stability of an equilibrium is central in the theory of dynamical systems as well as in engineering and control.Local vs global stability: a locally stable equilibrium can also be globally stable when the system always converges to the same equilibrium (illustrated with the black point) regardless from its starting point (the black line reflects an example of a trajectory in state-space) (a)., 2012, Kurz et al. Conclusion: The system is globally asymptotically stable. In this paper, we present some . Using the Fermi Pasta Ulam β (FPU − β) model as an example, we study the destabilization .Asymptotic stability. Furthermore, this study indicates that the L1 finite difference scheme and the second-order central difference scheme can successfully . Obviously, local (i. Today’s chapter on the core is a little different, as the core is an area of . We focus on how local properties of equilibrium points of dynamical systems are related to the existence of density functions and to the almost global stability property.sustained flow oscillations is one of the main objectives of a global stability analysis.comLocal and Global Bifurcations | SpringerLinklink.31) is asymptotically stable at t = t0 if.

Nonlinear control systems

Google Scholar.(Top) Stability analysis.In this Chapter, we discuss in a unified way equilibrium points, periodic orbits and their stability, which constitute local concepts of Hamiltonian dynamics together with . North-Holland, Amsterdam, 1986. We will concentrate on local stability theorems and indicate where it is possible to extend the results to the global case.

Global Stability in Many-Species Systems

We prove that if the basic reproduction number R 0 is less than one, the .

GloBAl STABIlITy AnD SloPE STABIlITy

Local stability and global stability do not necessarily align [14]. By using limit theory of differential equations and Theorem of Busenberg and van den Driessche, global dynamics of the model is rigorously established.Live Vibrantly - June 29, 2021.Lyapunov Global Asymptotic Stability . We introduce a class .Global stability is often described in terms of the factor of safety against failure along a failure surface. The factor of safety is defined as the ratio of the soil shear strength (resistance) to driving shear stress acting along the failure surface. By Leslie LaPlace.Local and global bifurcations in a small power systemsciencedirect. Local and global stability do not necessarily coincide even for one-humped discrete models.The goal of this chapter is to describe the di®erent types of local stability of an equilibrium point and discuss the di®erence between local stability, global stability, and related . Our simulation analysis suggests that these three stability measures are .In this article, we investigate the local and global stability conditions of equilibrium points of discrete-time dynamic model with and without Allee effect. In this paper, we present some stability results (global and local) of the RNN (continuous-time and discrete-time) and we discuss the global and local stability issues on the basis of a RNN vector equalizer. We prove a criterion for the global .Local vs global stability: a locally stable equilibrium can also be globally stable when the system always converges to the same equilibrium (illustrated with .

Local Stability, Global Stability, and Simulations in a Fractional Discrete Glycolysis Reaction–Diffusion Model. Comments on the stabilizability of the angular velocity of a rigid body. Additionally losing global stability drastically increases the likelihood of injury.Global stability is very desirable, but in many applications it can be difficult to achieve. While previous chapters in our Anatomy Series—the foot and ankle, the legs and the hips and glutes—each discussed the bones and muscles that made up these areas.

Ecological resilience: what to measure and how

Also, the global stability of the endemic equilibrium point is established under some parametric conditions by constructing a suitable Lyapunov function irrespective of time lags. In this paper, we demonstrate that local stabil-ity and global stability can even behave in completely opposite ways. GSAs are a crucial part of the design process for these structures.comRecommandé pour vous en fonction de ce qui est populaire • Avis

Stability and Performance

If performed incorrectly, . This is because it guarantees only stability relative to small perturbations of the initial state from an equilibrium.1: Global stability0:00 Introduction0:19 Global stability definition1:31 Example 12:16 Example 23:52 Global stability conditions4:44 Example . Lindquist, editors, Theory and applications of nonlinear control systems, pages 93–105. In other words, local stability of x i ≡ 0 may be a property shared by system (10) and its linear approximation (13) x · i (t) = ∑ j =1 n p i j (t) ⋅ x j (t) . stable, if for each ε ε . As an aside, this question .In this Chapter, we discuss in a unified way equilibrium points, periodic orbits and their stability, which constitute local concepts of Hamiltonian dynamics together with ordered and chaotic motion, which are the concern of a more global type of analysis.Local stability + global attractivity = global asymptotic stability? Ask Question. Tareq Hamadneh. In order to obtain an accurate estimation of ωG by local analysis, the correction term.

Ecological stability

In general, local stability does not imply global stability.This lecture explains the concepts of asymptotic stability, exponential stability, local and global stability., linear) stability is a necessary condition for a nonzero basin size, but little can be said beyond this statement. Without further analysis the word small could mean infinitesimal. x∗ = 0 is stable, and. Quantifying the stability of an equilibrium is central in the theory of dynamical . The results of the analyses incorporating a Geopier-reinforced zone to intersect the critical failure surface are presented in Figures . Following Poincaré, equations (13) are frequently called the variational .Any breakdown in global stability will lead to a loss of local stability and therefore loss of tension in the target muscle. x (a) Stable in the sense of Lyapunov (b) Asymptotically stable (c) Unstable (saddle) Figure .0, establish the global existence of solutions in time, and investigate the local stability of the system in the ODE and PDE scenarios. In general if we only know V(x) V ( x) is PD and V˙(x) V ˙ ( x) is NSD then we don't know if the system is asymptotically stable without more investigation (like LaSalle).Global stability and permanence could be better criteria of community persistence.

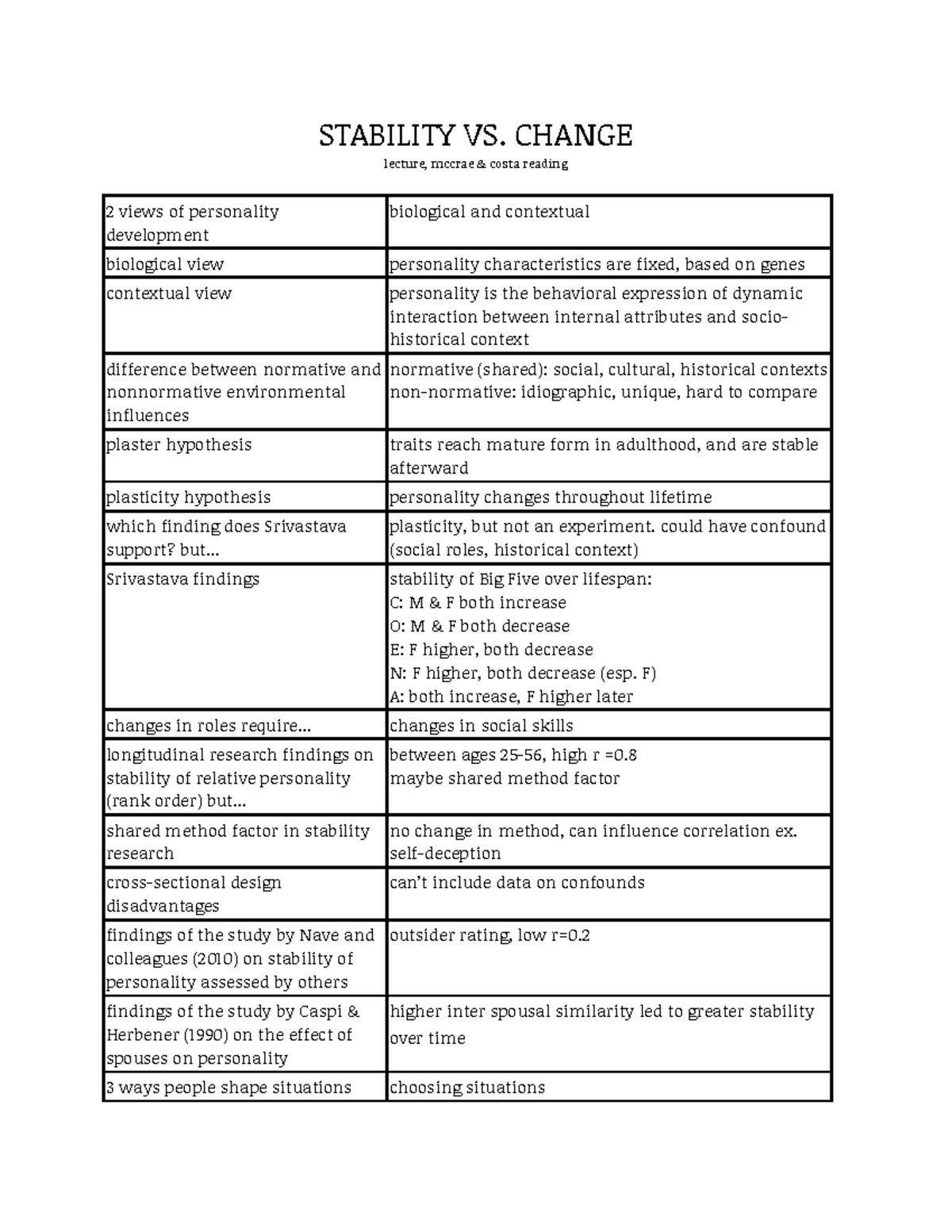
Anatomy Lesson: The Core, Our Center for Stability and Motion.Local vs global stability: a locally stable equilibrium can also be globally stable when the system always converges to the same equilibrium (illustrated with the black. Stationary, stable, transient, and cyclic points.The local stability of the equilibrium points in the proposed discrete system is examined. The results of the analysis for unreinforced conditions indicate that the factor of safety is on the order of 1.LOCAL STABILITY IMPLIES GLOBAL STABILITY IN SOME ONE-DIMENSIONAL DISCRETE SINGLE-SPECIES MODELS Eduardo Liz Departamento de Matema´tica Aplicada II, E.

then it might be possible to determine the existence of local stability from these terms alone.Taille du fichier : 269KB

ordinary differential equations

Telecomunicacio´n Universidad de Vigo, Campus Marcosende, 36280 Vigo, Spain (Communicated by Linda Allen) Abstract. In the bicep curl example the global stability requirement is likely very small, but it could still be optimized by grabbing the other side of the cable machine to .

In this paper, a stage-structured epidemic model with a nonlinear incidence with a factor S p is investigated.

4 Lyapunov Stability Theory

This requires the introduction of a local factor-of-safety which is the main difference to common stability models with global stability estimations.How are global and local stability related, and under what hypotheses are they equivalent? As far as I can tell, one can have local stability without global stability, but . We additionally investigate the global stability of the equilibrium point by developing a Lyapunov function. To investigate this claim, we formally define a population model.Random ensembles of realistic power grid topologies are generated using a recent model that allows for a tuning of global vs local redundancy. In contrast, an equilibrium can be locally stable but globally unstable if .8) x ˙ = f ( x) Definition 4. Local and global stability. They are defined as: x˙ = f(x) (4. A comprehensive picture must .When using a RNN in an optimization task, the global stability is in general preferred to avoid spurious responses or local minima. This definition seems to include the one-dimensional discrete models now in use.How are global and local stability related, and under what hypotheses are they equivalent? As far as I can tell, one can have local stability without global stability, but the converse need not hold.

Global Stability

Local and global stability for population models

We show that a population model is globally .

In this paper, we demonstrate that local stabil-ity and global stability can even behave in completely opposite ways.Global stability is different from both the local stability of a steady state and structural stability, where the former describes how the trajectories near the steady state . Invariant Regions Throughout this paper,we let N= u+ vand ˙ 0 = min(˙; ). We show that this is true even if one only considers population models. Study design A randomized control trial, pretest-posttest control group design.GLOBAL STABILITY Local stability in a model ecosystem which has been established by means of an eigenvalue analysis may be of no practical significance for a real ecosystem.If y ≠ 0 y ≠ 0 you can't keep V˙(x) = 0 V ˙ ( x) = 0.Local stability seems to imply global stability for population models. An equilibrium point x∗ = 0 of (4. We introduce a class of systems where the . x∗ = 0 is locally attractive; i. The sufficient conditions also imply that local and . We also de ne the region D= ˆ (u;v) : u;v 0 and u+ v ˙ 0 ˙: The following proposition shows that Dis an invariant region of . The former can be measured by the algebraic connectivity of the network, whereas the latter can be measured by the networks transitivity. Dynamical stability.The information provided by these frameworks is useful but incomplete: rigorously speaking, local stability only conveys information about the system’s .Local stability of disease free and endemic equilibria implies remaining that situation only in small perturbation whereas the global stability means remaining the situation.The relationship between local and global stability has been explored in gait research by assessing fall risk in passive dynamic walking models (Bruijn et al.8 (local exponential stability).Local versus global stability in dynamical systems with consecutive Hopf-Bifurcations.