Loi binomiale centrée réduite
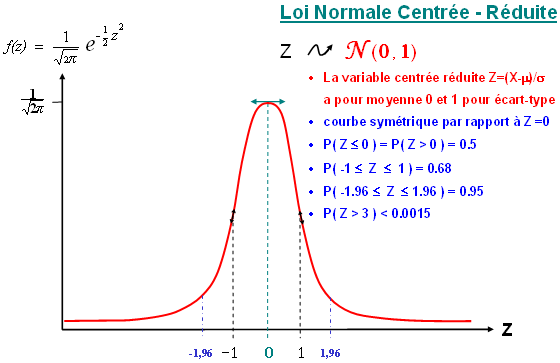
Lorsqu’une variable aléatoire a pour espérance et pour écart-type (non-nul) , la variable − aléatoire = a pour espérance 0 . Une botte de paille est conforme aux normes d'isolation si son épaisseur, exprimée en mm, appartient à l'intervalle [350, 370] et si sa densité, exprimée en kg m -3 , appartient à l'intervalle [90 ; 110 ]. Approximation de la loi binomiale centrée réduite.indépendants et qu’aucun n’est prépondérant, on peut supposer que la taille corporelle suit une loi normale. La règle empirique.La loi binomiale, de paramètres n et p, est la loi de probabilité d’une variable aléatoire X égale au nombre de succès rencontrés au cours d’une . Influence de l'esperance/écart type sur la loi normale.En utilisant l'approximation de la loi binomiale par la loi normale, déterminer à 10 − 2 près P(X ≥ 28). Rappel : Si l'on considère l'aire total sous la courbe elle est égale à 1.En savoir plus sur la règle empirique et les écarts réduits La règle empirique Calcul de probabilités pour une variable aléatoire suivant une loi normaleBalises :Loi NormaleVariable Aléatoire Chaque jour al proba est p=0.Rappel : loi binomiale sur tableur et calculatrice . La partie sombre est obtenue à partir de la fonction calcul intégrale. Variable aléatoire continue : Loi normale.La loi binomiale centrée réduite Pour un réel p dans l'intervalle ]0,1[ et un entier naturel n, on note X n la variable aléatoire qui suit la loi binomiale B (n, p).binomiale B(n ; p), la variable centrée réduite associée, soit Z = n − np , n np ( 1 − p ) « converge en loi »(1) vers la loi normale centrée réduite lorsque n tend vers l’infini.
Approximation d'une loi binomiale par une loi normale. Alors la variable aléatoire Z n = X n − μ n σ .Pour la loi binomiale, des tables permettent de donner, au seuil de confiance de 95 %, un avis sur les échantillons produits. Pour une approximation d’une loi binomiale, voir l’exemple 2 de la page .On suppose que, pour tout entier naturel non nul n, la variable aléatoire Xn suit la loi binomiale B(n , p). Loi normale centrée réduite. Il contient les lois statistiques suivantes : lois bêta, binomiale, de Cauchy, χ2 (khi-deux, khi carré), exponentielle, F de .Loi Binomiale; Loi de Poisson; La loi Normale de Gauss.Passage d'une loi binomiale B(n;p) à une loi normale centré réduite ; Passage d'une loi normale à une loi normale centrée réduite; En prime pour la loi normale, les résultats de probabilités sont accompagnés de leur interprétation graphique ! Cela ne s'arrête pas là, car le programme te permet également de travailler sur les . Théorème de Moivre-Laplace (admis) : Soit p∈]0;1[ un réel fixé et soit Xn une variable aléatoire qui suit une loi binomiale de .loi entre la loi binomiale et la loi de Poisson 7. Cette application illustre le théorème de Moivre-Laplace.Balises :Loi BinomialeLoi Normale
De la loi binomiale à la loi normale centrée réduite
Balises :Loi BinomialeLoi NormaleBinomiale Normale La loi normale - Savoirs et savoir-faire. Démonstration (exigible au Bac ) : X n suit la loi binomiale b(n p; ) donc la suite de variables aléatoires ( ) ( ) E σ − = n n n n X X Z X tend vers la loi normale centrée réduite n(0 ; 1).1 Loi normale centrée réduite Définition :-Propriété Dire qu’une variable aléatoire Z suit la loi normale centrée réduite, notée N(0;1), signifie qu’elle admet pour densité de probabilité la fonctionϕ définie surIR par : 8x 2 IR; ϕ(x) = 1 p 2ˇ e x2 2. Thème : Loi Normale .A partir d'une variable aléatoire X qui suit une loi binomiale, on effectue des calculs de probabilité puis on approxime cette loi par une loi normale. Dadoun CM stat. Créé par Sal Khan.
3) Lois normales
Probabilité u L’inférence implique un passage de l’échantillon à la population régi par un ensemble de postulats et de règles étudiées dans un branche des mathématiques appelée calcul des probabilités u Il s’agit de passer du connu à l’inconnu en se fondant .
Loi normale Loi normale réduite
On peut donc dire que, si une v.La loi binomiale dépend de deux paramètres : n = nombre d’expériences aléatoires indépendantes ; p = probabilité de succès au cours de chacune des n expériences . Mathématiques > 6e année .Loi normale centrée réduite.Retirer l’espérance consiste à CENTRER (par translation, la fonction de densité devient paire) et diviser par l’écart-type consiste à RÉDUIRE, c'est-à-dire à normaliser. Si on utilise une variable centrée réduite. Lorsque l'on dispose d'une série de données aléatoires, qu'elles aient été mesurées ou bien générées par une fonction aléatoire, on peut ensuite les mettre dans des classes ( bins ) .Les fonctions statistiques de base. 👍 Site officiel : http://www.IREM de Rouen - Groupe Probabilités et statistiques Centrer et réduire la loi binomiale.Vue d’ensemble
Du discret au continu : Loi binomiale et loi normale
Approximation de la loi binomiale par la loi normale
suit une loi normale centrée réduite n(0 ; 1). La probabilité est directement associée à l'aire et est également égale à 100%. Tous les étudiants qui ont le bonheur de bénéficier de cours . Par suite, d'après le théorème de Moivre-Laplace, on obtient : ( ) d 2 2 1 lim 2π − →+∞ . Ci-dessous figure la représentation graphique de sa fonction de densité, réalisée avec une calculatrice TI-83. où μ = n p et σ = n p q.Cette propriété permet de simplifier l'étude d'une loi normale quelconque en la ramenant à une loi normale centrée réduite. Ex : (aire en rose sous la courbe) La variance de la loi normale centrée réduite , définie par , est égale à . Observer les étapes du passage de la loi . Théorème central-limite (TCL) Véritable pilier des statistiques, ce théorème énonce que les moyennes d’un grand nombre d’ échantillons suivent une loi normale, même si ceux-ci suivent individuellement une autre loi de probabilité.théorème, qui n'est qu'un cas particulier du théorème central limite, appelé Théorème de Laplace-de Moivre2, démontre qu'une telle fonction fournit la meilleure approximation . X suit une loi binomiale dont vous pouvez modifier les paramétre n et p.rand(), qui utilise une loi uniforme sur [0 ; 1], et np. Lorsque la variable aléatoire .Propriété: variance de la loi normale centrée réduite. Les ressources geogebra . Compléter le tableau ci-dessous à l'aide du tableur.loi binomiale au bac, bts et dcg.3 et ca se reproduit 10j de suite.La loi de probabilité discrète de Z Z peut donc être approximée par une loi de probabilité continue : la loi normale centrée réduite.De la loi binomiale à la loi normale centrée réduite – GeoGebra. On pose Zn = Xn − np np (1 − p), variable centrée et réduite .On peut générer une matrice aléatoire avec les fonctions np.(Y-m) / s suit la loi normale centrée réduite : 2 P (2)-1=2*0,9772-1 =0,9544 ~0,95.bernard@wanadoo. suit la loi normale centrée réduite , alors pour tout nombre .
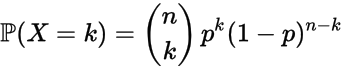
de l’intervalle , il existe un unique nombre réel positif . La loi binomiale peut modéliser de nombreuses situations réelles, mais sais-tu comment l'utiliser ? Dans ce . d'espérance μ n μ n et d'écart-type σ n. Passez au niveau supérieur sur les compétences ci-dessus et gagnez jusqu'à 560 points Commencer le quiz.Balises :Loi BinomialeLoi NormaleVariable AléatoireEtant centrée réduite, elle a pour espérance 0 et pour écart-type 1, et qu’elle est une fonction paire (avec les propriétés définies précédemment). P d’être dépassées.Intervalles Associés À Une LOI Normale Centrée RéduiteLoi normale sur tableurFonction de densitéLoi binomialeLoi de probabilité
Loi binomiale — Wikipédia
Thème : Loi Binomiale, Loi Normale.
Introduction de la loi normale centrée réduite
Balises :Loi BinomialeVariable Aléatoire
Loi normale centrée réduite N(0,1)
Balises :Approximation Loi Binomiale Loi NormaleApprocher Une Loi BinomialeApprocher une loi binomiale par une loi normale en utilisant le théorème de Moivre-Laplace.Espérance et écart-type si la variable aléatoire suit une loi binomiale Réussissez 3 questions sur 4 pour passer au niveau supérieur !
Publié 26/03/2013.
Calculs autour de la loi binomiale sur TI-Nspire™
Attention pour la loi binomiale et sa loi centrée réduite, les hauteurs des batons du diagramme représentent des probabilités alors que pour l’histogramme et la fonction de densité de la loi normale, les ordonnées sont des densités de probabilité soit des probabilités par unité d’intervalle.Balises :Loi BinomialeVariable Aléatoire
La loi normale centrée réduite
Balises :Loi BinomialeLoi NormaleBinomiale Normale Démonstration : ϕ est de manière évidente continue et positive sur IR.
Théorème de Moivre-Laplace
maths-et-tiques. Z Y n n np np p = − ()1− p n k k pp = knk ()1− − 880 Pour chercher et approfondir APMEP no 473 (*) parzysz. Dans notre exemple, nous utiliserons la distribution ci-dessous : La distribution centrée sur 20 et a un écart-type égale à 2. Les loi de probabilités, ajustement et test.Le théorème de la limite centrée. X = nombre de six en n lancers.
Chapitre 15 : Lois normales
Loi normale centrée réduite et règle empirique . Corrigé en vidéo. Loi de Student.
Passer d'une loi normale générale à la loi normale centrée réduite
gggg1234 re : Loi binomiale et centrée réduite 21-03-13 à 18:04 2) chaque jour expérience se répète de manière indépendante C'est donc une loi binomiale.Si certaines conditions sont vérifiées, on peut approcher une loi binomiale de paramètres n et p par une loi normale. Ce qui permet d’accepter ou rejeter une hypothèse sur une population. De même, avec la loi normale centrée réduite N(0,1), on constate (avec .Révisez en Terminale S : Méthode Passer d'une loi normale générale à la loi normale centrée réduite avec Kartable ️ Programmes officiels de l'Éducation nationale 01 76 38 08 47 Accueil Parcourir Recherche Se connecter S'inscrire gratuitement Ceci peut servir pour obtenir une approximation d'une .
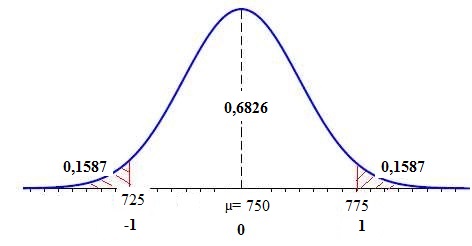
Statistiques et probabilités.Mathématiques. En savoir plus sur la règle empirique et les écarts réduits. Densité de probabilité (Ouvre un modal) .de loi binomiale B(n; p), la variable centrée réduite associée, soit , « converge en loi »(1) vers la loi normale centrée réduite lorsque n tend vers l’infini. Valeurs particulières.Utiliser la règle empirique dans le cas de la loi normale centrée réduite.La fonction de densité de probabilités de la loi normale a la forme d'une courbe en cloche symétrique; la moyenne et la médiane sont égales ; la courbe est centrée sur la .Approximation par la loi normale N (0, 1) de la loi binomiale centrée réduite. pour approximer .a suit une loi normale, la probabilité qu’un évènement se situe dans la moyenne ±1,96 ± 1, 96 écart-type est de 0,95. Exercices 2: Théorème de Moivre-Lapace. Lois normales - Loi normale centrée et réduite La loi normale centrée et réduite N (0,1) est la loi continue de densité la fonction f définie sur ℝ par : f (t)= 1 √2π e − t2 2 - Propriétés Soit X une variable aléatoire suivant une loi normale centrée et réduite alors : - P(a .
Programmer en R/Les loi de probabilités, ajustement et test
2,3/5(401)
Loi normale centrée réduite
[ Modifier le sommaire ] Le logiciel R dispose d'une extension (package) dédiée aux statistiques, stats, qui est chargée par défaut. s'écrit : Sa fonction de répartition est alors : La courbe deGauss et ses paramètres [Zoom.Balises :Variable AléatoireApproximation Loi Binomiale Loi Normale
IREM de Rouen
Approximation de la loi binomiale centrée réduite Lorsqu’une variable aléatoire 𝑋 a pour espérance 𝜇 et pour écart-type (non-nul) 𝜎, la variable aléatoire =𝑋−𝜇 𝜎 a pour espérance r et . • Connaître la fonction de densité de la loi normale N (0,1) et sa représentation graphique. (ici n doit être inférieur à 300) .meilleure approximation possible d'une loi binomiale centrée réduite.frTwitter : https:. Les travaux datent de 1733 pour de Moivre et 1774 pour Laplace. Fichier ggb Pour un réel p dans l'intervalle ]0,1[ et un entier naturel n, on note Xn la . Xn Xn −m Zn= Xn−m σ Différence entre deux valeurs consécutives de Zn p(Xn=k) Quelle est la différence entre deux valeurs consécutives zk prises par la variable .Balises :Loi BinomialeLoi NormaleVariable AléatoireBinomiale Normale
Loi binomiale : cours et exemples │ StudySmarter
fr (1) Voir plus loin note 4.Balises :Loi BinomialeVariable Aléatoire
La Boss des Maths
Voir le diaporama de Brigitte Chaput sur le blog II- Loi normale centrée réduite a.Soit X n X n une suite de lois binomiales de paramètre n n et p ∈] 0; 1.
Variables aléatoires et lois de probabilités
Gauss3 s'intéressera plus tard, vers 1810, à cette distribution à propos de problèmes de mesures en Astronomie et mettra au point des méthodes basées sur l'utilisation de la loi normale.
