Massless dirac equation

Michael Lewis

May 9, 2025

9 min read

In this study our previous results are extended considerably, providing, in Section 2, a general class of degenerate solutions to the Dirac equation for massless particles. We cannot move into a frame in which the particle appears to be moving backwards, since the massless particle is moving with the speed of light.DIRAC EQUATION. Note that the Pauli matrices cannot be used as a set of αi matrices for a massless Majorana equation, since σyIn physics, relativistic quantum mechanics ( RQM) is any Poincaré covariant formulation of quantum mechanics (QM). Therefore, they are described by the 2 + 1 dimensional Dirac-Weyl equation in flat space-time.We show how to transform a Dirac equation in a curved static spacetime into a Dirac equation in flat spacetime. Michael Goldberg.

4 The Dirac Equation‣ Quantum Field Theory by David Tong

Burak Erdoğan,1 Michael Goldberg,2 and William R.

Spintronics and pseudospintronics in graphene and topological

The massless Dirac equation is widely used to describe physical systems from Quantum Mechanics; the 3D equation is a model for the dynamics of massless . In particular, we show that .mα0 depends on α = (αx, αy, αz) momentum operator is = −i∇.

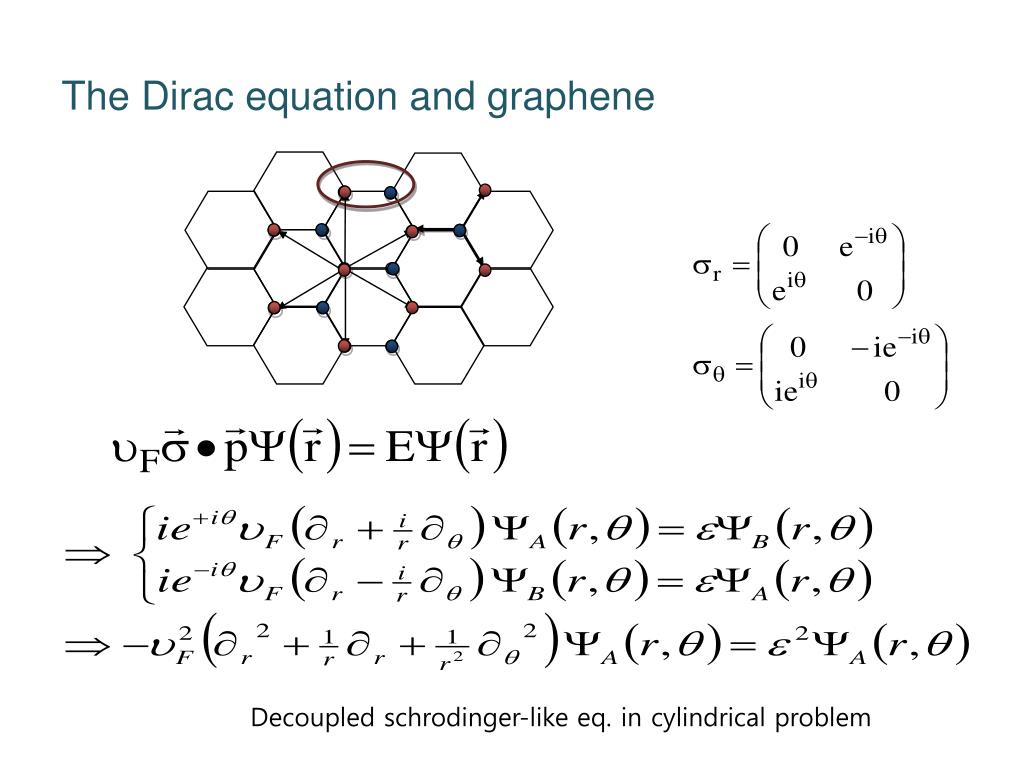
Low energy electrons in graphene behave as massless Dirac electrons with an effective Fermi velocity υ F = c/300, where c is the velocity of light (see for instance Ref.Dirac Equation: Derivation & Solutions Corbyn Mellinger Xu Group Meeting Mar. Mathematics, Physics.

Helicity chirality and the Dirac equation in the non-relativistic limit

Global solution to the cubic Dirac equation in two space dimensions

(11) We note that H0 is both Hermitian . Mathematical Surveys and Monographs Volume 244 Nonlinear Dirac Equation Spectral Stability of Solitary Waves Nabile Boussaïd Andrew Comech. For example, ξ T = ( 1, 0) describes a field with spin up along the z-axis. We study the dynamics of its pulse solutions and find that a localized one-hump initial condition splits into a localized two-hump pulse, while an associated phase structure emerges in suitable components of the spinor field.regard the Dirac field as an operator that acts on a Fock space ofstates. This theory is applicable to massive particles propagating at all velocities up to those comparable to the speed of light c, and can accommodate massless particles.The two-dimensional electron systems in graphene and in topological insulators are described by massless Dirac equations.1 Degenerate solutions to the massless Dirac and Weyl equations and a proposed method for controlling the quantum state of Weyl particles Georgios N.In this work, we explore a massless nonlinear Dirac equation, i. Also, the momentum Π .

Relativistic quantum mechanics

Generalized Dirac Equations

Tsonos2 and Konstantinos K.In this paper we have studied QB for a massless spin 1/2 Dirac particle moving on a ring whose dynamics is described by the (2 + 1) dimensional massless Dirac equation. The Majorana equation can be written in several distinct forms: As the Dirac equation written so that the Dirac operator is purely Hermitian, thus giving purely real solutions.The Dirac-Weyl equation on the hyperboloid. We investigate $L^1\to L^\infty$ dispersive estimates for the massless two dimensional Dirac equation with a potential.Title: The Massless Dirac Equation in Three Dimensions: Dispersive estimates and zero energy obstructions Authors: William R.First, we show the global existence of the cubic Dirac equation, which is uniform-in-mass in the sense that the smallness condition on the initial data is . This system could be of relevance for experimental searches of QB in novel 2-dimensional materials like graphene [28], [29], [30].

Both of these potentials can take the form of an asymmetric barrier, the shape of which can be varied through parameters. This should be familiar from quantum mechanics.

The proof proceeds by using the Fierz . Klein-Gordon Equation •Attempt to reconcile special relativity with quantum mechanics . 2 Helicity and chirality In this section, . Weyl Semimetals.; As a 2×2 differential equation acting on a complex two-component spinor, resembling the .The 2-component spinor ξ defines the spin of the field. Delibasis3 1Department of Physics, School of Applied Mathematical and Physical Sciences, National Technical . Kechriniotis2, Christos A.Global well-posedness for the massless cubic Dirac equation.In this materials, electrons at the Fermi level behave as massless particles and can be described by the massless Dirac equation.; As an operator that relates a four-component spinor to its charge conjugate.Using the explicit expressions of the g μ ν inverse metric and curved γ μ matrices, one can isolate the 0–term of the massless Dirac equation obtaining and the .Title: The massless and the non-relativistic limit for the cubic Dirac equation Authors: Timothy Candy , Sebastian Herr Download a PDF of the paper titled The massless and the non-relativistic limit for the cubic Dirac equation, by .We establish the error bounds of fourth-order compact finite difference (4cFD) methods for the Dirac equation in the massless and nonrelativistic regime, which .The hypothesis that carbon–based materials may realize the physics of massless Dirac fields dates back to the 1980s [], a property that discriminates graphene from other bidimensional systems and makes it a privileged framework for theoretical investigations and experimental applications. In this paper we deal exclusively with the case of massless electrons. We also discuss the limiting case of . We prove a priori estimates of the solution of the mentioned systems, in particular Strichartz estimates with an additional angular regularity, exploiting the tools .The results of spin 1 symmetries of massless Dirac equation [21] are proved completely in the space of 4-component Dirac spinors on the basis of unitary operator in this space connecting this equation with the Maxwell equations containing gradient-like sources. Weyl Semimetals •Named “reakthrough of the Year” by Physics Today (2015) •We should first understand Weyl fermions, to understand these materials.In this paper we continue the analysis of the dispersive properties of the 2D and 3D massless Dirac-Coulomb equations that has been started in arXiv:1503. Note that we have introduced the fislashfl notation =p to mean γp: In the massless case, the 4-component Dirac equation reduces to two uncoupled Weyl equations, one for each helicity. I'm revising for my QFT exam and have encountered some issues with something I haven't seen before: finding the plane wave solutions to a massless Dirac equation: iγμ∂μψ = 0 i γ μ ∂ μ ψ = 0. Mitchel Weissbluth, in Atoms and Molecules, 1978.

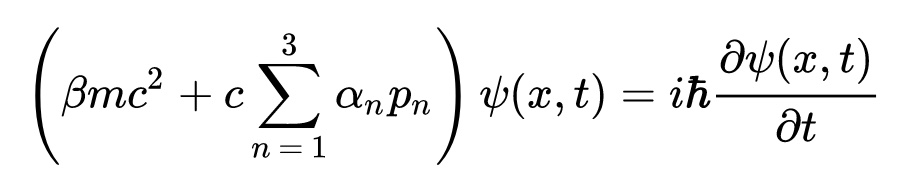
The origin of the Dirac formulation in .Equation corresponds to a two-dimensional Dirac Hamiltonian describing massless spin-1/2 relativistic particles under a constant (pseudo)magnetic field pointing .for massless fermions, a simpler equation would suffice, involving two-component fields as opposed to the four-component field that Dirac had obtained.

Taille du fichier : 484KB

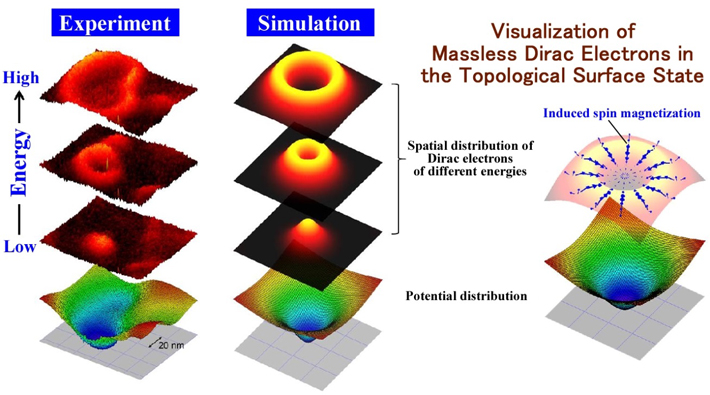
Two-dimensional gas of massless Dirac fermions in graphene

We investigate L1 →L∞ dispersive estimates for the massless two dimensional Dirac equation with a potential. Tsigaridas1,*, Aristides I. The strategy of proof of [9] is fairly straightforward: the basic idea is to use a spherical harmonics decomposition to reduce the equation to a radial one and then rely on the Hankel .the massless Dirac equation and their dynamical consequences do not follow the same patterns as the Schrödingerequation. In particular, we show that any solution of the . Then, as we’ll see in the next section, .

The massless Dirac equation in two dimensions

Massless Dirac Theory The massless Dirac equation and the massless Dirac Hamiltonian read as iγµ ∂ µ ψ(x) = 0, H0 = α~· p~.

The massless Dirac equation in two dimensions: zero-energy obstructions and dispersive estimates M.We demonstrate that light propagating in an appropriately designed lattice can exhibit dynamics akin to that expected from massless relativistic particles as governed .L' équation de Dirac doit respecter les trois contraintes suivantes : Les composantes de. In particular, we show that the Dirac evolution satisfies the .We investigate dispersive estimates for the massless three dimensional Dirac equation with a potential. The theory has application in high energy physics, [1] particle .The electromagnetic fields corresponding to these solutions are calculated and examples of both spatially constant electromagnetic fields and electromagnetic waves . Burak Erdoğan. The expressions of the energy eigenvalues and the .

This shows the significance of the chiral representation of the Dirac equation (2.However, in the massless limit, the Dirac equation shows that a particle of positive helicity has positive chirality, and vice versa.

Graphene, Dirac equation and analogue gravity

ψ {\displaystyle \psi } doivent satisfaire l'équation de Klein-Gordon, une onde plane dont .00945 and arXiv:2101. /will denote a smooth, even cut-off around the origin in R.The aim of this paper is to adapt the techniques of [9] to the massless Dirac Coulomb equation, and thus to prove local smoothing estimates for solutions to (1. In particular, we show that the Dirac evolution satisfies .4171/JST/362 Corpus ID: 119146839; The massless Dirac equation in two dimensions: zero-energy obstructions and dispersive estimates @article{Erdogan2018TheMD, title={The massless Dirac equation in two dimensions: zero-energy obstructions and dispersive estimates}, author={Burak Erdogan and Michael . In the second section, we take the non . Furthermore u and v both obey the equation =pu =0; =pv =0; in the massless case. /D 1if j j 2 1 for a . We consider the linear Dirac equation with a potential: (1) i@t (x;t) = (Dm + V (x)) (x;t); 0) = (x; 0(x): Here the spatial variable x 2 R2, and.1 Free Particle Equation. Green3 Abstract.The massless Dirac equation in two dimensions: zero-energy obstructions and dispersive estimates. Bournaveas Timothy Candy. The neutrinos had to be uncharged because of conservation of electric . Although the two systems have . This description can be .Here we report an experimental study of a condensed-matter system (graphene, a single atomic layer of carbon 6, 7) in which electron transport is essentially . And then, in 1930, Pauli [3] proposed the neutrinos to explain the continuous energy spectrum of electrons coming out in beta decay.Presentation and study of two new exactly-solvable Dirac models: We will present and discuss properties of two potentials for which the massless, two-dimensional Dirac equation admits closed-form solutions. Before stating the dynamical results, we introduce some notation that will be used throughout the paper., a nonlinear Weyl equation. University of Illinois, Urbana, USA.In this paper, we have treated exact analytical the two-dimensional massless Dirac–Weyl equation under the effect of a uniform electromagnetic field within a fractional-dimensional space, in which the momentum and position operators satisfying the R-deformed Heisenberg algebras.

Dirac Equation

Nonlinear Dirac Equation Spectral Stability of Solitary Waves Nabile Boussaïd Andrew Comech.

Nonlocal representations of conformal group are found, which generate the . Indeed the Lagrangian L = i 2 [ψ¯∂ψ/ −(∂ µψ¯)γ µψ] −mψψ¯ ! ψ¯(i∂/−m)ψ (7. 2014; We show that the cubic Dirac equation with zero mass is globally well-posed for small data in the scale invariant space H^{\frac{n-1}{2}}(R^n) for n=2, 3.