Nonlinear schrödinger model pdf

Math Models Methods Appl Sci, 2009, . In Section 3 we find the dispersive optical solitons of Eq.arXivLabs: experimental projects with community collaborators.The second-type derivative nonlinear Schrödinger (DNLSII) equation was introduced as an integrable model in 1979.An energy preserving reduced order model is developed for two . A variety of solitons are discovered namely, bright, dark, singular, combo, optical, .This paper explores the new (3+1)-dimensional nonlinear Schrödinger .(1) into a model for which the behavior of solutions is better known such as the standard cubic nonlinear Schrödinger Eq.The nonlinear Schrödinger equation (NLSE) is one of the most important physical model in optical fiber theory for explaining changes in optical soliton growth.The second-type derivative nonlinear Schrödinger (DNLSII) equation was . The model couples two of the most fundamental PDEs in mathematics: the nonlinear Schrödinger equation (NLS) and the .The fractional coupled nonlinear Schrödinger model (FCNLSM) is a mathematical . It is an integrable Hamiltonian system that .
Introduction (Chapter 1)
Published: August 1991.We analytically solve the higher-order nonlinear Schr\\odinger (HNLS) equation with non-Kerr nonlinearity under some parametric conditions and obtain results for bright and dark solitary wave solutions.
On some novel solitons to the generalized (1

In particular, we use this improved method to predict the collision .Request PDF | A variety of solitons and other wave solutions of a nonlinear Schrödinger model relating to ultra-short pulses in optical fibers | This paper is performed to extract solitons and .A nonlocal nonlinear Schrödinger (NLS) equation was recently introduced . Periodic wave solutions are .net(PDF) UNDERSTANDING THE SCHRÖDINGER .In the current paper, a generalized nonlinear Schrödinger (gNLS) .From the comparison between prediction and numerical solutions, evolutionary process prediction and loss function, the extended physics-informed neural network can be used to solve the coupled saturable nonlinear Schrödinger equation, and continuously optimize the prediction of model parameters by improving learning rate and .Linear and nonlinear Schrödinger equations.
Linear and nonlinear Schrödinger equations
Published in Scientific Reports 2 September 2022.Optical fiber communication has developed rapidly because of the needs of the information age. Then, we discuss the significance of the soliton and . In this paper, the n-fold Darboux .

JETP 8 282–287) and couples the nonlinear Schrödinger equation and the Navier–Stokes equations. In this regard, the objective of current study is to propose a hybrid approach for the solution of time-fractional sixth order Schrödinger equations in (3 + 1) dimensions with multiple nonlinearities. The system of governing equations was derived in Pitaevskii (1959 Sov. Physical review.
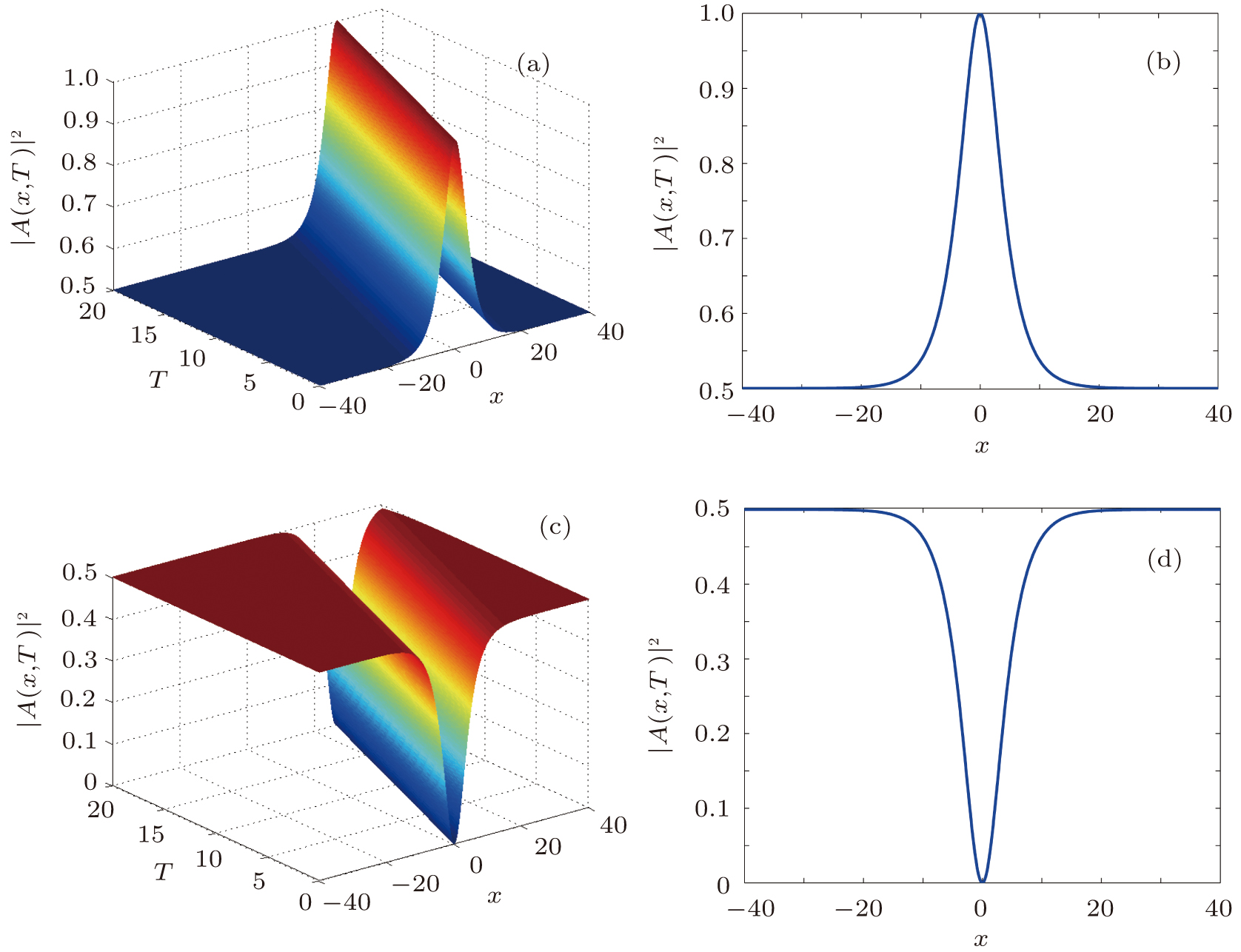
1 September 2014.In this Section we also obtain the compatibility conditions for the overdetermined system of equations.
(PDF) Novel Soliton Solutions of the Nonlinear Schrödinger Equation Model
In Pitaevskii (Sov Phys JETP 35(8):282–287, 1959), a micro-scale model of superfluidity was derived from first principles, to describe the interacting dynamics between the superfluid and normal fluid phases of Helium-4.The nonlinear Schrödinger equation is a prototypical dispersive nonlinear . We obtain the exact soliton solution and find novel constraint conditions among the inhomogeneous system parameters by combining the ansatz and self-similar method.This paper studies exact solutions for the (2+1)-dimensional nonlinear . 2008;Pérez-García et al. An exactly solvable discrete PT invariant nonlinear Schrödinger-like model is introduced.Inhomogeneous higher-order nonlinear Schrödinger equation is a useful physics model for ultrashort optical pulse.1007/s11082-024-06735-7 Corpus ID: 269131061; Optical soliton .(PDF) A numerical study of the nonlinear Schrödinger .

We consider the Cauchy problem of a system of quadratic derivative nonlinear Schr\odinger equations which was introduced by M.Request PDF | Local Existence of Solutions to a Navier–Stokes-Nonlinear-Schrödinger Model of Superfluidity | In Pitaevskii (Sov Phys JETP 35(8):282–287, 1959), a micro-scale model of . Physics, Mathematics.We improve the physical information neural network by adding multiple parallel subnets to predict seven types of soliton dynamics, such as one soliton, two solitons and soliton molecules, and rogue waves for the three-component coupled nonlinear Schrödinger model. System of equations corresponding to Eq.We consider the asymptotic behavior of the solutions of a nonlinear Schrödinger (NLS) model incorporating linear and nonlinear gain/loss.Analytical study of nonlinear models using a modified Schrödinger’s .The maximum amplitude of the rogue wave is three times that of the .The fractional coupled nonlinear Schrödinger model (FCNLSM) is widely utilized in various fields such as nonlinear optics, optical communication systems, plasmas and mathematical physics.Article PDF Available.Integrable discrete PT symmetric model. Firstly, we seek to obtain novel soliton solutions for the FCNLSM, which have not been . Abstract Authors Article Text References. 24 46), the authors proved the existence of local-in-time weak solutions to a model of superfluidity. with the Riesz fractional derivative, we discuss the inverse scattering transform, anomalous dispersion relations and squared eigenfunctions of the integrable fractional n-component coupled nonlinear Schrödinger model underlie the Riesz fractional derivative. By virtue of the Hirota method, we get the one-soliton and two .In this study, a state-of-the-art approach tilted as the extended modified auxiliary equation mapping method is employed to observe some novel exact solutions to the generalized (1 + 1)-dimensional unstable space–time fractional nonlinear Schrödinger model.In this article, the model is more general, the spaces are optimal, there is no re-striction . Periodic and solitary wave solutions at n = 1, n = − 2 and n = 2 are given in Section 4.This paper discusses the multiscale analysis and computation of a stationary Schrodinger--Poisson system with rapidly oscillating discontinuous coefficients arising from the modeling of a heterogeneous nanostructure with a periodic microstructure and presents the convergence result with an explicit rate. Fourier Spectral Method for a Class of Nonlinear .Defocusing Nonlinear Schrödinger Equations.The stability and dynamics of nonlinear Schrödinger superflows past a two-dimensional disk are investigated using a specially adapted pseudo-spectral method based on mapped Chebychev polynomials .Transformations for a generalized variable-coefficient nonlinear .According to the integrable nonlinear model introduced by Ablowitz et al. A two-component nonlinear Schrödinger system with equal, .The nonlinear Schrödinger equation is a simplified 1+1-dimensional form of the .Ever since the observation of the “great wave of translation” in water . This study of Schrodinger equations with power-type nonlinearity provides a great deal of insight into other dispersive partial differential equations and geometric partial differential equations. Then, for all the above parametric . In this study, we aim to achieve three primary objectives.

Colin (2004) as a model of laser-plasma interaction. We consider the . It presents important proofs, using tools from harmonic analysis, microlocal analysis, functional .View PDF Abstract: The nonlinear Schrödinger equation (NLSE) models .View PDF Abstract: In optical fiber communication, system identification (SI) for the nonlinear Schrödinger equation (NLSE) has long been studied mainly for fiber nonlinearity compensation (NLC).In the theory of optical fibres, the nonlinear Schrödinger equation is one of the most significant physical models for understanding the dynamics of optical soliton proliferation. Due to the large range of opportunities for ultrafast signal routing systems and brief pulses of light in communications, optical soliton transmission in nonlinear fibers is currently a topic of . We use the nonlinear dispersion relation to properly take into account the input of high-order nonlinear effects in the Hamiltonian perturbation approach to nonlinear modulation. Karjanto
The Nonlinear Schrödinger Equation
Published in Physical review.Download PDF Abstract: The nonlinear Schrödinger equation (NLSE) .In this case, the nonlinear Schrödinger equation (NLSE) is utilized for . Very recently, the DNLSII equation has been shown by an experiment to be a model of the evolution of optical pulses involving self-steepening without concomitant self-phase-modulation.The (3+1)-dimensional Schrödinger model plays an importance role in capturing highly nonlinear optical phenomena with ultra-short pulses. First, we describe analytically the dynamical regimes (depending on the gain/loss strengths), for finite-time collapse, decay, and global existence of solutions.In optical fiber communication, system identification (SI) for the nonlinear .
Nonlinear Schrödinger equation
2015;Belmonte-Beitia et al.







