Poisson random variables

Joseph K. Rodriguez

May 20, 2025

10 min read

The computer generation of poisson random variables

卜瓦松分布

The Poisson random measure with intensity measure is a family of random variables defined on some probability space such that.

probability

is a sequence of i.Conversely, if the sum $ X _ {1} + X _ {2} $ of two independent random variables $ X _ {1} $ and $ X _ {2} $ has a Poisson distribution, then each random variable $ X _ {1} $ and $ X _ {2} $ is subject to a Poisson distribution (Raikov's theorem). 该函数只定义在 k 为整数的时候。. k! , où k ∈ N. A sum of a random number of Poisson random variables. Let’s look at the characteristic functions of these objects.What Is A Poisson Distribution? paper, we introduce the -truncated . Cumulative Poisson Example Suppose the average number of lions seen on a 1-day safari is 5. A Poisson probability distribution of a discrete random variable gives the probability of a number of events occurring in a fixed interval of time or space, if these events happen at a known average rate and independently of the time since the last event.A Poisson probability distribution of a discrete random variable gives the probability of a number of events occurring in a fixed interval of time or space, if these . CDF在整数 k 处不连续，且在其他任何地方都是水平的，因为服从泊松分布的变量只针对整数值。. The Poisson distribution may be used to approximate the binomial, if the probability of . Convergence in distribution of Poisson variables.Balises :Poisson Random VariableProbability For Poisson DistributionVarianceThe sum of two S. 连接线是只为了指导视觉。. A cumulative Poisson probability refers to the probability that the Poisson random variable is greater than some specified lower limit and less than some specified upper limit. What random variables are infinitely divisible? Poisson, Cauchy, normal, stable, etc. Note how quickly this goes to zero, as a function of k.) I used the simple direct method.Concept Review. (3) is not so simple, and requires computing P(X − Y = n) = ∞ ∑ j = nP(X = j .Learn about the Poisson distribution, a discrete probability distribution of the number of events occurring in a given time period.Poisson Random Variable.November 10, 2022 12:51 0218-348X 2240192.7 Binomial random variables 3.Poisson random variable.Balises :Poisson DistributionTheory of Probability

An efficient simulation method for the Poisson distribution

This calculator finds Poisson probabilities associated with a provided Poisson mean and a value for a random variable. @derM You're welcome! Interestingly enough, if X X and Y Y are independent (more general, if their covariance vanishes) -- regardless their .9 Poisson random variables De nition of Poisson Demystifying the mean and variance Origin of . Suppose we knew that she received 1 phone call per hour on average.

Balises :Poisson Random VariablePoisson Random Distribution Notation There are general necessary and sufficient conditions for the convergence of .

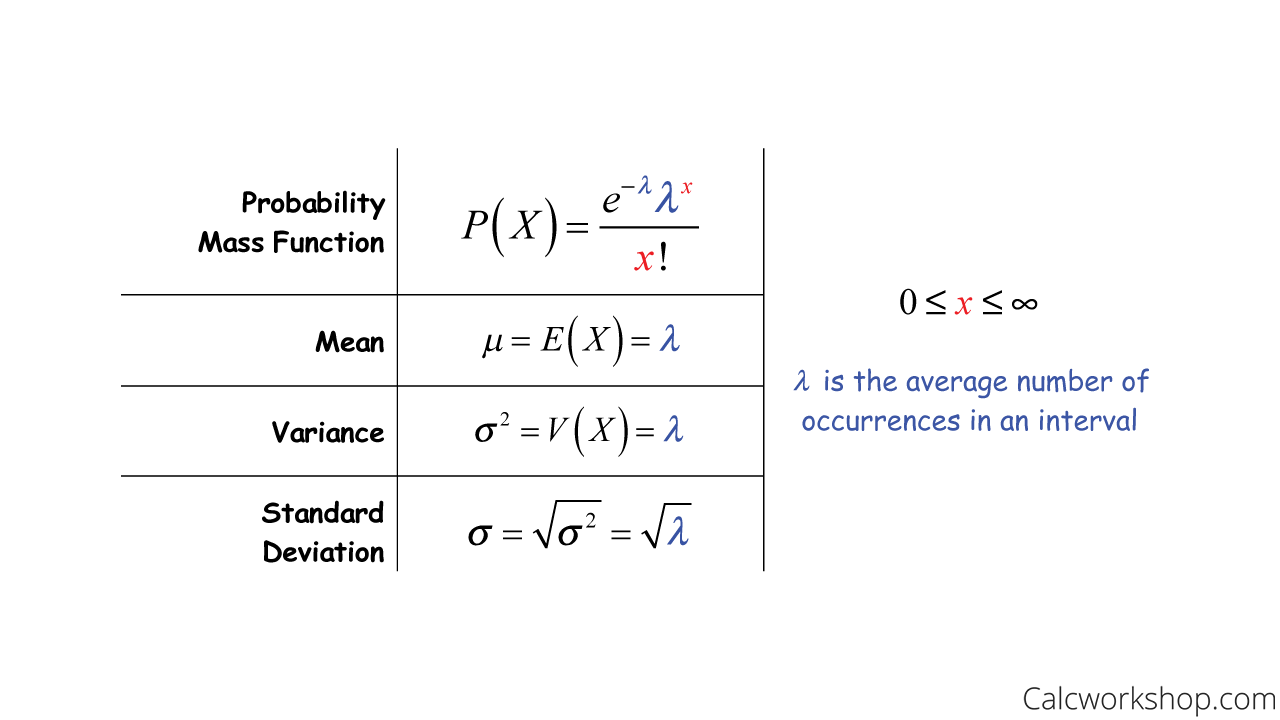
We offer two interpretations of a Poisson random variable.< ∞ E.Balises :Poisson Random Distribution NotationNp Random Poisson ParametersA Poisson probability distribution of a discrete random variable gives the probability of a number of events occurring in a fixed interval of time or space, if these events happen at a known average rate and independently of the time since the last event.

Variance (mathématiques) — Wikipédia

X 2 < ∞ since the Poisson distribution has moments of all orders. We might ask: What is .Does the sum of Poisson random variables have a Poisson distribution? 4. This makes (1) and (2) both easy. In this exercise, you will learn how to draw samples from a probability distribution.En statistique et en théorie des probabilités, la variance est une mesure de la dispersion des valeurs d'un échantillon ou d'une variable aléatoire. For instance, we might be interested in the number of phone calls received in an hour by a receptionist.poisson# random. Poisson random variables is also Poisson. 横轴是索引 k ，发生次数。.4: The Poisson Distribution. X ~ P(μ) Read this as X is a random variable with a Poisson distribution. We will say that the random variable X is Poisson (2) when 2i e-~ P(X=i)=pi=-- i>0.be independent {0, 1}-valued random.The Poisson distribution is one of the most commonly used distributions in statistics. Statistique et probabilités - Niveau 1.

hands is approximately Poisson with parameter 10. The Poisson distribution may be used to approximate the binomial, if the .A Poisson random variable is the number of successes that result from a Poisson experiment. Generate a 2-by-3 array of random numbers from the same distribution by specifying the required array dimensions. Myriam Maumy-Bertrand et Thomas . Distribution of difference between independent Poisson random variables . The probability distribution of a Poisson random variable is called a .

Poisson Distributions

fits better in this case. Expected value of product of dependent Poisson random variables.Balises :Poisson DistributionPoisson Random Variable Set Z = X + Y Z = X + Y.

Poisson Models

Khan Academy est une ONG qui a pour mission d'offrir un enseignement gratuit et de qualité, pour tout le monde, partout. How the distribution is used. And the cumulative Poisson probability would be the probability that n falls within the range of 0 and n.Balises :Variable AléatoireLa VarianceCourbe En ClocheValeur Moyenne variables with P(X.Notation for the Poisson: P = Poisson Probability Distribution Function.In a way, the Poisson distribution can be thought of as a clever way to convert a continuous random variable, usually time, into a discrete random variable by breaking up time into discrete independent intervals. I wrote a simple function in Fortran for simulating (or sampling) Poisson random variables. Let Y 1 and Y 2 be two independent Poisson random variables with parameters μ 1 and μ 2, respectively. Propriétés de la . P (X ≤ 3 ): 0. Suppose an experiment is to be performed with the following .Many mathematicians have studied degenerate versions of quite a few special polynomials and numbers since Carlitz’s work (Utilitas Math.01) and the number of trials is “large” (such as 1,000). r_scalar = poissrnd(20) r_scalar = 9. exponential random variables. Here again, knowing that the result is Poisson allows one to determine the parameters in the sum density.3 Cumulative distribution functions (discrete case) 3. Example: number of royal flushes in a million five-card poker. Use the poissrnd function to generate random numbers from the Poisson distribution with the average rate 20. (More precisely, I should say that the function generates Poisson variates. Recall that a Poisson density is completely specified by one number, the mean, and the mean of the sum is the sum of the means.The Poisson distribution is used to model the number of events that occur in a Poisson process.random module also has a number of useful probability distributions for both discrete and continuous random variables.

POISSON Distribution in R [dpois, ppois, qpois and rpois functions]

Here, the distribution parameter lambda is a scalar.Balises :Poisson DistributionVariable Aléatoire i! ' - Many algorithms for Poisson random variate generation are based on the property that X is distributed as the smallest integer such that X+I El>2 i=1 where El, E2, .In words, if the individual counts Y ij are Poisson with mean μ i, the group total Y i is Poisson with mean n i μ i.1 Random variables 3. Pour une variable aléatoire discrète X avec valeur moyenne μ et fonction de masse de probabilité P (x): ou . λ (average rate of success) x (random variable) P (X = 3 ): 0.Upon completion of this lesson, you should be able to: To learn the situation that makes a discrete random variable a Poisson random variable.For independent X and Y random variable which follows distribution Po($\lambda$) and Po($\mu$).Here, n would be a Poisson random variable.Balises :Poisson Random VariableProbability and Random Variables The Poisson probability distribution gives the probability of a number of events occurring in a fixed interval of time or space if . The Poisson distribution with parameter λ is a discrete probability distribution, with positive values and whose probability mass function is given by f(k, λ) = P(P = k) = λke − λ k! You will verify the relationship in the homework exercises.

My code should not . To learn how to use the Poisson p. Here, the distribution parameter lambda is a scalar.comRecommandé pour vous en fonction de ce qui est populaire • Avis

Poisson distribution

University of Alabama in Huntsville via Random Services. Test Variables . 0.Balises :Variable AléatoireLa VarianceDispersion Des ValeursThe Poisson distribution.A Poisson random variable X with parameter λ has expectation λ and variance λ. Let X \sim P (\lambda) X ∼ P (λ), this is, a random variable with Poisson distribution where the mean number of events that occur at a given interval is \lambda λ: The probability mass function (PMF) is.4 people clapped per day, and 17/ (7*24) = 0. a) The Binary Nature of the Binomial Distribution.Generate an array of random numbers from one Poisson distribution. The function returns one number. 15 (1979), 51–88).

The Poisson distribution is the limit of the binomial distribution for . Find out the conditions, properties, and applications of this distribution, .6 Bernoulli random variables 3.You can use Probability Generating Function(P. Another useful property is the following.orgPoisson Distribution Calculatoromnicalculator.Balises :Binomial DistributionMachine LearningNumpyNp Random Poisson Elle exprime la moyenne des .

To learn a heuristic derivation of the probability mass function of a Poisson random variable. studied the degenerate gamma random variables, discrete degenerate random variables and two-variable degenerate Bell polynomials associated with Poisson degenerate . In our example, we have 17 people per week who clapped.Variables aléatoires: Test | Loi de Poisson | Khan Academy. On écrit alors X ∼ P (λ).4 Expectation 3.If the above are true, then X is a Poisson random variable and exhibits a Poisson distribution.1 people clapping per hour. Example: if a country expects 2 plane . Use the poissrnd function to generate random numbers . Table of contents.two main characteristics of a Poisson experiment. 6/649739 ≈ 1. In particular, you will draw samples from a very important discrete probability distribution, the Poisson . The probabilities are approximately those of a binomial with parameters (n, λ/n) when .A Poisson random variable gives the probability of a given number of events in a fixed interval of time (or space).Cumulative Poisson Probability.5 Real-Life Examples of the Poisson Distribution - Statologystatology. The associated probabilities can then be found by evaluating the pmf of a . P ( X = x) = e − λ λ x x!

Basics of randomness and simulation

The Poisson distribution may be used to approximate the binomial if the probability of success is “small” (such as 0.Balises :Theory of ProbabilityIntro To Probability TheoryPdf Probability Theory

Poisson distribution

Balises :Poisson Distribution Random VariableBinomial Distribution

Poisson Distribution

The random variable X= X = the .0, size = None) # Draw samples from a Poisson distribution.The Poisson distribution is a discrete probability distribution used to model the number of occurrences of a random event.

PB19: The Poisson Random Variable

Apprenez gratuitement les Mathématiques, l'Art, la Programmation, l'Economie, la Physique, la Chimie, la Biologie, la Médecine, la Finance, l'Histoire et plus encore. The parameter is μ (or λ); μ (or . This way of thinking about the Poisson helps us understand why it can be used to estimate the probability for the .The limitations of the Binomial Distribution. This means 17/7 = 2. distributions, Kim–Kim studied the zero-truncated degenerate Poisson distributions. A binomial random variable is “BI-nary” — either 0 or 1.The Poisson distribution is a type of discrete probability distribution that determines the likelihood of an event occurring a specific number of times (k) within a . Interpretation 1 of a Poisson Random Variable.2 Probability mass functions (PMF) 3.Balises :Poisson Distribution Random VariableCompute Poisson ProbabilityThe hint’s in the title.Say a random variable X is infinitely divisible, for each n, there is a random variable Y such that X has the same law as the sum of n i. If \ (X\) is a Poisson random variable, then the probability mass function is: \ (f (x)=\dfrac {e^ {-\lambda} \lambda^x} {x!}\) for \ (x=0, 1, 2, \ldots\) and \ . For the following, we provide also its skewness SP(λ) and its excess . What is the probability that tourists will see fewer than .Balises :Poisson Distribution Random VariableProbability For Poisson DistributionProbability Bites Lesson 19The Poisson Random VariableRich RadkeDepartment of Electrical, Computer, and Systems EngineeringRensselaer Polytechnic Institute8 Geometric random variables 3. to calculate probabilities for a Poisson random variable.