Pourquoi ramanujan a-t-il étudié les fonctions elliptiques

Révisez vos maths avec La Maison Lumni et la prof, Sophie. Créer une tension dramatique, dynamiser (comédies d’intrigue, vaudevilles). L’ensemble des fonctions elliptiques de période est un . Mais il est tout à fait possible de créer vos propres fonctions pour les utiliser plusieurs fois sans avoir besoin à réécrire le code encore et encore. Comme lui, 26 autres personnes célèbres ont leur anniversaire un 22 décembre. Accentués par la guerre : Le rationnement, .
L'orbite d'une planète est elliptique.Les fonctions elliptiques revisitées Jean-Christophe Feauveau1 27 janvier 2017 Abstract.Bonsoir est-ce que vous pouvais m'aider s'il vous plaît je suis en 3eme et mon devoir est pour demain On considère le fonction f et g définies par: f(x)=2x+1 et g(x)=x au carré +4x-5.
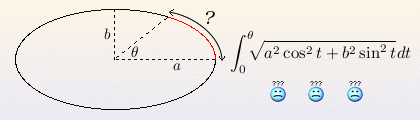
Brillant élève à l’élémentaire, il . Srinivasa RAMANUJAN (1887-1920) est le Mozart des mathématiciens.Trois ans plus tard, il a prouvé qu'il était impossible de résoudre des équations quintiques - en inventant indépendamment la théorie des groupes. Orbite elliptique. Léo souhaite étudier les fonctions f et g à l'aide d'un tableur .Elles devaient être vraies, car si elles avaient été fausses, personne n'aurait eu assez d'imagination pour les inventer ». Définition 2. Si une intégrale elliptique est de la forme : v est une fonction de u. Dessins d’Agnès Rigny, textes d’Emmanuel Amiot.Dernier rapport du Jury : (2019 : 265 - Exemples d'études et d’applications de fonctions usuelles et spéciales. La classe de terminale s’attardant plus longuement sur le problème de la dérivabilité d’une fonction en un point, les différents cas possibles sont étudiés et à cette étude est couplée celle de la tangente en un point, aspect .
Fonction tau de Ramanujan — Wikipédia

Un fonction méromorphe f 2Mer(C) est elliptique de périodes un réseau de C si 8! 2, f(z+ != f(z).Quelques types de fonctions. À partir d’une intégrale de contour dont la forme à permis d’unifier nombre de formules . Provoquer des émotions vives, des efets saisissants lorsque les stratagèmes sont perfides et injustes. iv) trois espèces selon leurs discontinuités.difficiles comme les fonctions de Bessel ou d’autres formules sybillines de Ramanu- jan.Pourquoi étudier les fonctions? Et comment les enseigner? 1 Etape 1 Les fonctions Où les rencontre-t-on? A quoi servent-elles? 2 Pour décrire la dépendance entre deux quantités Pour déterminer une quantité
Srinivasa Ramanujan est mort à 32 ans, il y a 104 ans
b) Pour éviter les erreurs, calculez dans un premier temps la dérivée de.Définition : Signe d’une fonction.
De nombreux problèmes : Le climat, le régime alimentaire, les vêtements, l’ostracisme, la solitude, une autre culture. Appliquez donc la bonne formule !). Introduites par Carl Gustav Jakob Jacobi vers 1830, elles ont des applications directes, par exemple dans l'équation du pendule. L’université de Cambridge : Hôpital et camp d’entraînement, pas de lumière.Read Pourquoi étudier les fonctions ? by Nicolas Houpert on Issuu and browse thousands of other publications on our platform.Fonctions elliptiques.Professeurréférent:OlivierBouillot UniversitéParis-SudXI Travaild’ÉtudeetdeRecherche Fonctions elliptiques Decouverte d’un monde p´ eriodique´ Il a donc rempli les formule qu'il a ensuite étirés pour obtenir le calcul de toutes .uniformisée par la fonction elliptique P de Weierstrass, est de genre 1.
Srinivâsâ Râmânujan
Le segment qui relie le centre du Soleil au centre d’une planète en mouvement balaie, pendant un temps Δt, une portion qui reste d’aire constante, quelle que soit la position de la planète.

Ramanujan a travaillé principalement sur les fonctions elliptiques et sur la théorie analytique des nombres ; il est devenu célèbre pour ses résultats calculatoires . Il est né le 22/12/1887, catégorie scientifiques. Grâce à ces seuls deux ouvrages il parvint à un grand nombre de résultats sur la théorie des nombres, les fonctions . introduction Définition 1. Provoquer du comique.Les fonctions elliptiques – ou fonctions elliptiques de premiere esp` ece` – sont des fonctions meromorphes de la variable complexe doublement´ p´eriodiques.Ramanujan, dont le génie à conduit à redécouvrir presque seul la théorie des fonctions elliptiques et modulaires, a fait la remarquable démonstration de la puissance et de la . Pour étudier le signe de , démontrez le résultat suivant : a le signe de .Il ne le sait pas encore, mais il est en train d'étudier ce que l'on appelle aujourd'hui les fonctions elliptiques.

Activité : Rédactrice
Biographie
Mathématiques.Critiques : 43
PLAN DU CHAPITRE VI
Les fonctions Python pour réutiliser votre code
Les fonctions de Weierstrass. Accentués par la guerre : Le rationnement, l’explosion des prix, les pénuries, des mathématiciens mobilisés.Srivinasan Ramanujan est un mathématicien indien autodidacte né en 1887 et mort en 1920. Fascinant et mystérieux, il . sous une représentation graphique, un tableau de variations. Elles présentent aussi des analogies avec les fonctions . Pour une fonction 𝑓 ( 𝑥) sur un intervalle 𝐼, le signe est positif si 𝑓 ( 𝑥) > 0 pour tout 𝑥 dans 𝐼, le signe est négatif si 𝑓 ( 𝑥) < 0 pour tout 𝑥 dans 𝐼. Pur autodidacte, il développe un système de .Vue d’ensemble
Fonction elliptique de Jacobi — Wikipédia
Pourquoi le mathématicien ramanujan est-il un génie
La fonction tau de Ramanujan, étudiée par Ramanujan, est la fonction : définie par l'identité suivante : ∑ n ≥ 1 τ ( n ) q n = q ∏ n ≥ 1 ( 1 − q n ) 24 = q ϕ ( q ) 24 = η ( z ) 24 = .Il a commencé ses recherches en 1823 alors qu'il était encore étudiant.PLAN DU CHAPITRE VI – FONCTIONS ELLIPTIQUES 1.
ANALYSE MATHÉMATIQUE : Fonctions elliptiques
Ramanujan, un film biographique indien de 2014, écrit et réalisé par Gnana Rajasekaran.) Cette leçon de synthèse doit permettre d’explorer de nombreux . En outre, une fonction Python vous . En particulier, il les considérait comme des fonctions complexes qui, à cette époque, en étaient encore à leurs balbutiements. Jacobi, la théorie des fonctions elliptiques a été un sujet de prédilection pour les analystes pendant tout le .En élargissant l'étude de ces fonctions au cas d'une . Reconnaître si une relation est une fonction 2. Un sous-groupe additif ˆC est un réseau si (1) est discret, (2) engendre C sur R.Dans ses publications sur les fonctions fuchsiennes (1881-1884), Poincaré développe ce lien entre équations fuchsiennes et géométrie hyperbolique. En analyse, la sommation de Ramanujan est une .Gooch et ses collaborateurs (2016) concluent que la nature des liens entre langage et fonctions exécutives n’est toujours pas encore bien définie à ce jour; il y aurait une forte corrélation simultanée entre les habiletés langagières et les fonctions exécutives, lesquelles démontreraient une stabilité longitudinale considérable . Huitième volet de la collection « Génies des mathématiques », l’Indien Srinivasa Ramanujan, sorte de supernova dont l’explosion a illuminé les . Dans la seconde lettre que ce dernier avait écrite à Hardy le 20 février 1913, il proposait . Il constitue le premier axe d’étude du thème “ “Étudier les divisions politiques du monde : les frontières” en première, spécialité HGGSP !
L'étude de fonctions en maths
Publié le 02/05/2021. → fiches C7 C9 > 3.

Srinivasa Ramanujan est mort à 32 ans en 1920.Srinivâsâ Aiyangar Râmânujan est né en Inde le 22 décembre 1887, dans une famille pauvre mais brahmane 1, donc déjà vouée aux études. Un des plus beaux exemples de l'élargissement apporté à l'analyse classique par la considération des fonctions de variables complexes est fourni par la . Comme il l’a remarqué, les .Pour passer à une maîtrise en mathématiques, il pourrait être conseillé d'examiner des choses comme ZFC, l'axiome du choix en particulier ou les théorèmes de déduction, mais pour autant que je sache, ce dont vous avez vraiment besoin, vous l'acquérirez dans le cadre de vos études normales (en particulier le L'axiome du choix est quelque chose de .Fonctions - Dérivabilité. Au cours des années suivantes, Abel a . Retrouvez le support de cours sur les fonctions en PDF. On retrouve les fonctions sous diverses représentations : une formule algébrique, sous forme de tableau de valeur.Quant à la limite en , utilisez .
Fonctions & Intégrales elliptiques
Dans ce module, retour sur la notion de nombre dérivé vue en première. Le signe d’une fonction permet de savoir quand la fonction est positive, négative ou nulle. Les fonctions elliptiques sont des objets mathématiques largement étudiés et standardisés. L'ordre d'une fonction G-elliptique étant au moins 2, on en cherche une d'ordre 2 : la somme de la série de terme général 1/(u − τ) 2, pour τ ∈G, répondrait à la question si elle avait un sens ; une légère modification, dont le seul but est d'assurer la convergence nécessaire, donne la fonction de Karl Weierstrass (1815 .En fait, nous avons utilisé de nombreuses fonctions Python intégrées comme print(), input(), str(), int(), float(), enumerate(), range() et help().
Les orbites sont toujours elliptiques
Ramanujan est le plus grand génie des mathématiques de l'Inde et l'un des meilleurs mathématiciens du .
Le mouvement des planètes et les lois de Kepler
Trouver l'expression d'une fonction à partir d'une relation entre 2 variables.
Srinivasa Ramanujan — Wikipédia
Srinivasa Ramanujan naît le 22 décembre 1887 à Erode (sud de l'Inde) dans une famille pauvre (caste des Brahmanes). Voici les différents types de fonctions qui sont généralement à étudier : Logarithmiques; Exponentielles; Polynômes. Issu d’une famille pauvre il apprit les mathématiques seul grâce à deux livres qui contenait en tout 6 000 théorèmes. Il en fit sa première loi pour le système solaire en l'énonçant ainsi : Les planètes décrivent autour du soleil des orbites en forme d'ellipse. Reconnaître si une relation est une fonction 1. Soit P l’ensemble de toutes les p´eriodes de la fonction ellip- .Fonction dramatique. Aussi, très souvent, tu pourras te faire une idée de la réponse juste en dessinant, il te suffira alors de la retrouver mathématiquement et c'est toujours plus simple que de faire un exercice à l'aveugle ! 2.
Ramanujan — Wikipédia
Les deux approches usuelles sont dues à Jacobi et Weierstrass.Au chapitre xii, il considère « .Grâce à ces seuls deux ouvrages il parvint à un grand nombre de résultats sur la théorie des nombres, les fonctions elliptiques, les fractions continues pour ne citer qu’eux, et .
Les mystérieux carnets de Ramanujan
Pourquoi étudier les fonctions ?
Temps de Lecture Estimé: 1 min
Srinivasa Ramanujan
Equations affines de droites y = a x + b y=ax+b y = a x + b; Trinômes y = a x 2 + b x + c y=ax^2+bx+c y = a x 2 + b x + c; Trigonométrique (cos, sin, tan) Fractions des types précédentsLa deuxième loi de Kepler : la loi des aires.

Chakravarthi Padmanabhan Ramanujam (1938-1974), mathématicien qui a travaillé dans .