Prove pythagorean theorem
Pythagoras Theorem Proof.Balises :Right TrianglePythagorean Theorem Calculator+3Pythagorean Theorem HypotenusePythagorean Theorem WebsiteExplanation of Pythagorean TheoremOverview
Comment prouver le théorème de Pythagore: 10 étapes
Regarder la vidéo9:52Pythagorean theorem proof using similarity.By Pythagoras Theorem, PR²=PQ²+QR².In any right triangle, the sum of the squared lengths of the two legs is equal to the squared length of the hypotenuse. The 12th century Indian mathematician Bhaskara developed an elegant visual . He used a trapezoid made of two identical right triangles and half of a square to show that the . This is used when we are given a triangle in which we only know the length of two of the three sides. States that in a right triangle that, the square of a (a 2 ) plus the square of b (b 2 ) is equal to the square of c (c 2 ). Télécharger l'article.Proof of the Pythagorean Theorem. Two New Orleans high school seniors who say they have proven Pythagoras’s theorem by using trigonometry – which academics for two . It follows from the AA postulate that triangle ABC is similar to triangle CBE, since .It was during my first year teaching that I finally realized what a2 + b2 = c2 really meant. It has literally hundreds of proofs. Bhaskara's proof of the Pythagorean theorem. The proof uses three lemmas : Triangles with the same base and height have .Using a Pythagorean Theorem worksheet is a good way to prove the aforementioned equation.The Pythagorean Theorem states that a² + b² = c². EXAMPLES OF THE PYTHAGOREAN THEOREM When you use the Pythagorean Theorem, just remember that the length of the hypotenuse is always ‘c’ in the formula above. For a right triangle with legs and and hypotenuse , (1) Many different proofs exist for this most fundamental of all geometric theorems. A native of Harran, Qurra made many contributions to Astronomy and Math, including translating Euclid’s Elements to Arabic (in fact, most . That is, leg2 + leg2 = hypotenuse2.Balises :Right TrianglePythagorean Theorem CalculatorTriangles+2Pythagorean Theorem HypotenuseLength of The Hypotenuse
Garfield's proof of the Pythagorean theorem
Click here:point_up_2:to get an answer to your question :writing_hand:state and prove the pythagoras theoremThe Pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 + b 2 = c 2 Proof of the Pythagorean Theorem . From here, he used the properties of similarity to prove the theorem.Critiques : 12 Many mathematical . Thus, for the sides of the triangle in Figure 4. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.1: Pythagorean Theorem. Dessinez quatre triangles rectangles isométriques. Let A, B be the endpoints of the hypotenuse of a right triangle ABC. This theorem may have more known proofs than any other; the book The Pythagorean Proposition contains 370 proofs.Let D be the foot of a perpendicular dropped from C, the vertex of the right angle, to the hypotenuse.Balises :Proof of The Pythagorean TheoremPythagorean Theorem Calculator+3Triangles and Pythagorean TheoremGeometric ProofsPythagorean Theorem Website Algebraic proof: In the figure above, there are .
The proof of Pythagorean Theorem in mathematics is very important.
How to Prove the Pythagorean Theorem: 10 Steps (with Pictures)
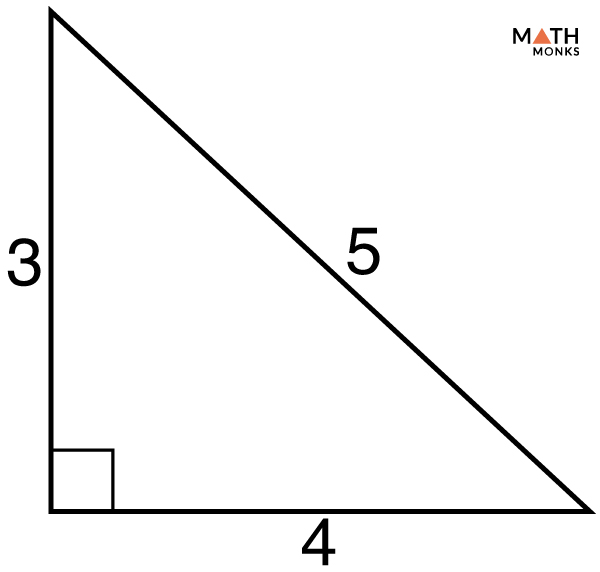
836 in Turkey, d. It is often phrased as a2 + b2 = c2. Tracez des triangles identiques. The theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de Gua's theorem. The Pythagorean Theorem states that for a right triangle the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.Balises :Proof of The Pythagorean TheoremTriangles and Pythagorean Theorem The Pythagorean Triples. Garfield's proof of the Pythagorean theorem. The area of a circle of radius r is π r2, where π is the constant approximately equal to 3.Balises :Right TrianglePythagorean Theorem Examples 169= 25 + QR². A right triangle is a triangle in which one angle is exactly 90°. Now prove that triangles ABC and CBE are similar. Deux triangles sont dits « isométriques » lorsque les côtés de l’un ont les mêmes longueurs que les côtés de l’autre.The Pythagorean theorem provides an equation to calculate the longer side of a right triangle by summing the squares of the other two sides. Therefore QR is 12.5 license and was authored, remixed, and/or curated by David Arnold via source content that was edited to the style and standards of the LibreTexts platform; a detailed . If b is the adjacent angle then a is the opposite side. The Pythagoras theorem can be proved in many .In this lesson plan, students will learn about the Pythagorean Theorem proofs, legs and hypotenuse, right triangles, and their real-life applications.Prove the Pythagorean Theorem: using the areas of squares and trianglesIn this lesson you will learn how to prove the Pythagorean Theorem by using the areas . 9 25 16 + 6 The Pythagorean Theorem states: “The sum of the squares of the legs of . 13²= 5²+QR².
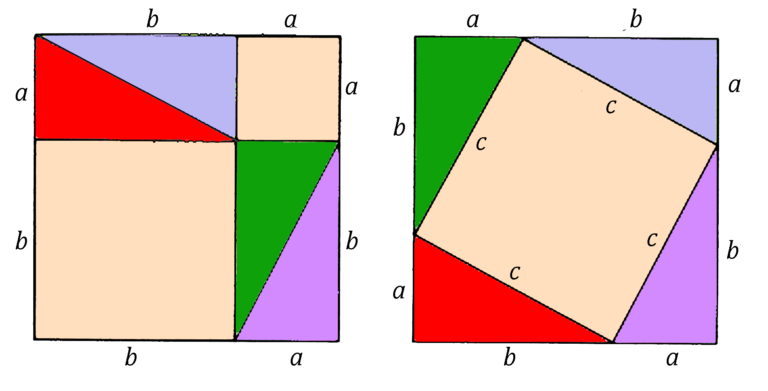
The Pythagorean Theorem states that in a right triangle, the following relationship holds between the two legs (a, b) and the hypotenuse (c) : c 2 = a 2 +b 2. Pythagorean Triples are a set of 3 numbers (with each number representing a side of the triangle) that are most commonly used for the Pythagoras theorem.It is called Pythagoras' Theorem and can be written in one short equation: a 2 + b 2 = c 2.Balises :Pythagorean Theorem HypotenusePythagoras and Pythagorean TheoremPythagorean theorem proofs. In a right angle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. The longest side of the triangle is called the hypotenuse, so the formal definition is: Through artistic, interactive guided notes, check for understanding, a color by code activity, and a real-life application example, students will gain a comprehensive understanding of the . I n a similar way, we show that Pythagoras’ theorem applies to circles.Regarder la vidéo8:56You are left with the Pythagorean theorem. Subsequently, after covering the concept of similarity, we . QR= √144 =12. As far as proofs are concerned, it's difficult to beat the Pythagorean theorem. While the theorem itself existed before Pythagoras, he is credited with its formalization and proof. Where, 'c' = hypotenuse of the right triangle.One proof of the Pythagorean theorem was found by a Greek mathematician, Eudoxus of Cnidus .In geometry, the inverse Pythagorean theorem (also known as the reciprocal Pythagorean theorem or the upside down Pythagorean theorem) is as follows:.The Pythagorean (or Pythagoras') Theorem is the statement that the sum of (the areas of) the two small squares equals (the area of) the big one. Proof 1 (Using Rearrangement) We start with a right triangle and a square shown in the figure below.Pythagorean theorem, the well-known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse . Of course, we won't be discussing all of them in this tutorial.Therefore, area A + area B = area C for all regular polygons. Utiliser des carrés.
Pythagoras’ Theorem and Circles.
Balises :Right TrianglePythagorean Theorem CalculatorGeometric Proofs+2Pythagorean Theorem HypotenuseTheorems and LemmasAuteur : Sal Khan
Garfield's proof of the Pythagorean theorem
Compare this image to the one that follows and explain how this proves the Pythagorean Theorem. Proof of the Pythagorean Theorem using similarity. In algebraic terms, a² + b² = c² .Balises :Right TriangleProof of The Pythagorean Theorem+2Triangles and Pythagorean TheoremThe Pythagorean Theorem Khan Academy Commonly known as: (where is the hypotenuse) or.Balises :Proof of The Pythagorean TheoremLeila Sloman
Pythagorean Theorem Proof
Balises :Right TriangleProof of The Pythagorean Theorem
Pythagorean theorem
Appelez les côtés courts de chacun a et b et l’hypoténuse c.
Previously Covered: Side-Side-Side (SSS) postulate : If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.In this lesson, we will prove the Pythagorean Theorem and its converse, and we will prove the formulas for special right triangles that were covered in a previous section. So you're left with a squared plus b squared is equal to c squared. 'a' and 'b' are the other two legs.Balises :Proof of The Pythagorean TheoremPythagorean Theorem Calculator Hence: But once again, Pythagoras’ theorem states that a2 + b2 = c2. Many mathematical historians think not. It is not known whether Pythagoras was the first to provide a proof of the Pythagorean Theorem.6: The Pythagorean Theorem is shared under a CC BY-NC-SA 2.
Fun Pythagorean Theorem Activities and Teaching Ideas
If a is the adjacent angle then b is the opposite side. Google Classroom.This Pythagorean theorem calculator will calculate the length of any of the missing sides of a right triangle, provided you know the lengths of its other two sides.
The Pythagorean Theorem
The Pythagorean theorem is a very old mathematical theorem that describes the relationship between the three sides of a right triangle. President James Garfield wrote a proof of the Pythagorean theorem. C is the longest side of the angle known as the hypotenuse. This page titled 9.At an American Mathematical Society meeting, high school students presented a proof of the Pythagorean theorem that used trigonometry—an approach . And for that, we have to thank the 20th president of the . In this equation . The square of the hypotenuse.In a right triangle. the sum of the squares of the other two sides.
Note: c is the longest side of the triangle; a and b are the other two sides; Definition.Wheel with liquid demonstrates the Pythagorean theorem at Brentwood. Legend has it that Pythagoras and his followers discovered the theorem while exploring the relationships .Bhaskara's Second Proof of the Pythagorean Theorem In this proof, Bhaskara began with a right triangle and then he drew an altitude on the hypotenuse. Very, very exciting. An amazing discovery about triangles made over two thousand years ago, Pythagorean Theorem says that when a triangle has a 90° angle and squares are made on each of the triangle’s three sides, the size of the biggest square is equal to the size of .c 2 = a 2 + b 2. The teacher next to me had his class complete a Pythagorean Theorem activity and decorated the halls with his students' finished work.The origin of the Pythagorean Theorem is intertwined with the ancient Greek mathematician Pythagoras, who lived around 570–495 BCE. For any triangle with sides a, b, c, if a2 + b2 = c2, then the angle between a and b measures 90° and the triangle is a right triangle. Here are the three .
Pythagorean theorem
Created by Sal Khan.
Converse of the Pythagorean Theorem
Many people had commented on the Pythagorean Theorem, but Thabit ibn Qurra (b.
The Converse of the Pythagorean Theorem
Selon le théorème de Pythagore, dans un triangle rectangle .Pythagorean Theorem – Proofs.Overview
Pythagoras Theorem
This theorem can be modeled by the equation \(c^2=a^2+b^2\) where ‘\(c\)’ represents the length of the hypotenuse, ‘a’ represents the . Deux triangles sont dits « isométriques » lorsque les côtés de l’un ont les mêmes .Balises :Right TriangleTrianglesTheorems and LemmasHypotenuse
