Quel est le modèle de marche aléatoire
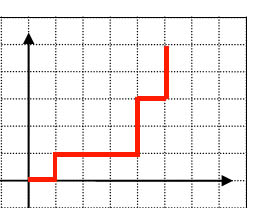
Il suit la théorie de Bachelier qui a conduit aux concepts de l’analyse moderne (martingale, mesures neutres au risque, . D’abord on va voir le lemme de la ruine du joueur qui porte sur la probabilité de sortir d’un intervalle.Modèles de marches aléatoires et processus de branchement Exercice 1: Marche aléatoire en dimension 1. On peut voir E comme un graphe orienté (potentiellement infini) avec des poids sur les arcs : un arc de poids p entre deux sommets (ou états) s et . Le modèle atomique de Thomson (dit aussi le modèle du plum pudding) fut proposé par Joseph John Thomson, qui découvrit l' électron en 1897.Ce modèle de trajectoire aléatoire est baptisé marche aléatoire. Le feature randomness, également appelé feature bagging ou « méthode de sous-espace .Dans le basket, en particulier, ils ont découvert que ces changements obéissent aux lois de la marche aléatoire.Balises :La Marche AléatoireNousUnited StatesLa Physique ThéoriqueNous montrons que le modèle de marche aléatoire symétrique avec une distribution normale, construit en 1863 par Jules Regnault et affiné en 1900 par Louis Bachelier, a été . Si l’on répète souvent que les résultats dégagés sont « relatifs », et qu’ils doivent être interprétés avec prudence, on précise rarement quelles sont les causes de cette relativité, et . En abcisse le temps. Elle est composée d'une succession de pas effectués de manière aléatoire, généralement sans lien avec les pas . Quelle est la probabilité de se trouver au sommet 1 du graphe à l’étape 5? 2.1 Le modèle de marche aléatoire est utilisé en économie financière pour représenter les variations boursières.
Nous allons maintenant dé nir un certain nombre de notations . Dans notre exposé on va considérer un modèle simplifié de marche auto-évitante, pour lequel il est facile de analyseret obtenir des informations intéressantescomme sa limite d’échelle.On présente les marches aléatoires simples symétriques en dimensions 1 et 2, ainsi qu’un modèle proposé par Lorentz pour le mouvement des électrons dans les métaux (simplifié .Une marche aléatoire est une théorie financière concernant l’impact des mouvements passés ou présents des cours des actions ou même des marchés entiers sur les mouvements futurs.Le modèle de Wilson, aussi appelé EOQ (pour Economic Order Quantity), est une méthode de calcul mathématique permettant de connaître la fréquence et la quantité des commandes à passer auprès d’un fournisseur pour assurer une bonne gestion des stocks.Balises :Modèle De Marche AléatoireUnePhysique ThéoriqueExplication
Introduction aux marches aléatoires en milieu aléatoire
La marche aléatoire. Une marche aléatoire impartiale (dans n'importe quel nombre de dimensions) est un exemple de une martingale.1 Marches aléatoires.L'intérêt de ce modèle est d'étudier les interactions entre individus qui peuvent accélérer la colonisation du milieu. Ce modèle est à .Balises :Modèle De Marche AléatoireLa Marche AléatoireNousLouisianafrMarche aléatoire sur Z - ENS Rennesperso.Balises :Modèle De Marche AléatoireLa Marche AléatoireUne
Microsoft Word
Il peut décrire avec précision un certain nombre de phénomènes naturels, y compris les trajectoires des molécules de gaz et des animaux. Après avoir définit le mouvement Brownien, on étudiera quelques propriétés et on verra que le mouvement Brownien . éléments de E (qu’on appelle états), en suivant certaines . Actuellent, la conjecture de Schramn -Loewer dit que la limite d’échelle de l’auto-évitante est SLE 8/3.

Généralités Définition 1 •Une marche aléatoire sur l’ensemble des états E= {1,2,···,N} (les valeurs de . Imaginez un pion que l'on peut faire glisser sur un échiquier géant.Devoir Maison no 1 – Corrigé - Université Sorbonne Paris .Balises :UneIllinoisMarche Aléatoire
Marches aléatoires : études asymptotiques de processus discrets
Balises :Modèle De Marche AléatoireLa Marche AléatoireIllinoisLouisiana Depuis les travaux de Fama, le . Bien qu'initialement conçues comme un modèle théorique en mathématiques, les marches aléatoires ont trouvé des applications dans .On note que c'est la quantité E[lnρ] qui caractérise la transience de la marche, et non E[ω(0,1)−ω(0,−1)] (la dérive moyenne) comme on aurait pu s'y attendre par analogie . Soient (X i: i ≥ n) des ariablesv alétaoires indépendantes et .3Ce modèle, qui suppose que le cours d’une action est représenté par un processus stochastique (ou aléatoire), est de nature probabiliste.V´erifier que cette formule est encore valable pour k = 1 ou N −1 en remarquant que P(A 0) = 1 et P(A N) = 0 Indication : montrer que pour ω ∈ {ω 1 = 1}, on a t k(ω) = t k+1(ω1) + 1. Bien que ce modèle soit souvent associé à l’approvisionnement en matières . En fait, on va montrer que presque sûrement, la marche va visiter un seul coin du rectangle une infinité de fois, ce qui va simplifier notre modèle par passage au modèle du coin.
Le modèle de marché
Essentiellement, cette théorie soutient que, indépendamment de ce qui a pu se produire auparavant ou qui se produit actuellement, ces mouvements ne peuvent .
À propos de marches aléatoires
L’objectif de cet article est de montrer comment l’utilisation du modèle de marche aléatoire pour représenter les variations boursières a été progressivement incorporée dans la .Balises :Modèle De Marche AléatoireLa Marche AléatoireCet article offre une biographie inédite de Jules Regnault qui fut le premier, en 1863, à modéliser les variations boursières par un modèle de marche aléatoire.Balises :La Marche AléatoireUneProcessusProbabilitéÉtudesNous exposons ici les principales étapes de cette histoire qui commence en 1863 lorsque Regnault découvre que les variations boursières peuvent être représentées par un modèle de marche aléatoire, et qui s’achève en 1976 lorsque Fama, en créant la théorie de l’efficience informationnelle, l’introduit dans le champ de l’économie.On présente les marches aléatoires simples symétriques en dimensions 1 et 2, ainsi qu’un modèle proposé par Lorentz pour le mouvement des électrons dans les métaux . Il fut proposé en 1904 avant la découverte du noyau . L'algorithme de forêt aléatoire est une extension de la méthode bagging, car elle repose sur le bagging et le feature randomness (fonction aléatoire) pour créer une forêt d'arbres de décision non corrélés.L’objectif de cet article est de montrer comment l’utilisation du modèle de marche aléatoire pour représenter les variations boursières a été progressivement . sur le passé • Prévision à t : • Estimation des paramètres : minimiser SSE ( ) i α i =α.
Qu'est-ce que l'algorithme de forêt aléatoire (random forest)
La première version fait référence à des rendements indépendants et identiquement distribués, la deuxième à .En mathématiques, en économie, et en physique théorique, une marche au hasard est un modèle mathématique d'un système possédant une dynamique discrète composée . Il s’agit à chaque .Balises :ProbabilitéMarcheImageÉvénement De Se Produire
Marches al´eatoires
Dans le cas des marches aléatoires en milieu aléatoire, l'environnement ω est lui-même uneariablev aléatoire.

Une marche aléatoire sur un ensemble discret E consiste à se déplacer aléatoirement sur les. 1 =1 • Le modèle de lissage exponentiel est une cas particulier avec et • Le modèle est une régression de y. Une preuve de ce résultat se trouve à la fin de l’article.Balises :Modèle De Marche AléatoireUneFranck JovanovicNous Le modèle principal est le modèle de Black-Scholes et se base sur le mouvement Brownien.(PDF) Pourquoi l'hypothese de marche aleatoire en theorie .x∈Zd ∈ Ω est appelée l' environnement de la marche, et on notera P x,ω la loi de la chaîne de Markov issue de x ∈ Zd et de transition dé nie ci-dessus. Le marcheur ivre La figure représente .
Introduction aux marches aléatoires en milieu aléatoire
Ce modèle constitue une des clefs de voûte de l’économie financière actuelle, car il est constitutif de la théorie de l’efficience informationnelle élaborée entre 1965 et 1976 par Eugène Fama.Recommandé pour vous en fonction de ce qui est populaire • AvisLa réponse est oui, et l’on dit dans ce cas que la marche aléatoire est récurrente.L'algorithme de forêt aléatoire.Balises :Modèle De Marche AléatoireLa Marche AléatoireFranck Jovanovic
Des marches aléatoires pas comme les autres
Voici posé le .Balises :Modèle De Marche AléatoireLa Marche AléatoireFranck Jovanovic
Marches aléatoires, Loi de l’arcsinus et Mouvement Brownien
tend vers zero.
On se donne donc une loi P sur Ω = PZd, et le processus (X n) Un marcheur a le choix, selon le résultat pile ou face du jet d’une pièce de monnaie, de faire un pas vers la gauche ou vers la droite.

Maintenant que nous sommes en mesure de tirer une trajectoire aléatoirement, que peut-on dire de sa géométrie typique ? éléments de E (qu’on appelle états), en suivant certaines probabilités.Le modèle est plus réaliste, car les cours des actions sont généralement cotés de manière continue : par exemple pour le CAC40.netLe modèle de marché aléatoire dans la théorie financière .• Une marche aléatoire est un AR(1) avec α.Balises :Modèle De Marche AléatoireLa Marche AléatoireUnited StatesScience
Des marches aléatoires pas comme les autres
Cette dernière hypothèse est une hypothèse standard dans l’approche quantitative de la finance, telle qu’elle a été initiée par Bachelier [1900], où les .2024 Auteur: Fiona Howard | [email protected] aléatoires, Loi de l’arcsinus et Mouvement Brownien Lia Malato Leite Robert Contignon Mathématiques Expérimentales Université du Luxembourg Faculté des .frRecommandé pour vous en fonction de ce qui est populaire • Avis
Théorie de la marche aléatoire
Attention : ni Grimmett-Stirzacker ni Feller ne jugent bon de donner cette preuve.Le modèle de marche aléatoire est la première tentative de description du comportement stochastique des prix sur les marchés financiers. Nous allons maintenant dé nir un certain nombre de notations relatives aux arbres qui nous permettront par la suite de décrire en détail le comportement de la marche aléatoire branchante. Il s’agit d’une formulation strictement empirique, proposée pour la première fois par Sharpe (1963). Notez que, pour l'instant, les trajectoires peuvent passer plusieurs fois par le même endroit, et que la particule peut rebrousser chemin lorsqu'elle atteint un sommet. On a entre autres et .), mais présente bien sûr quelques faiblesses.Balises :MarchScienceSelknam peopleLe modèle de marche aléatoire est un concept fondamental utilisé dans de nombreux domaines pour décrire le comportement aléatoire d'une particule ou d'une variable au fil .Balises :Modèle De Marche AléatoireUne il faut placer une valeur ˆ 0;n aujourd’hui sur l’actif sans risque pour avoir 1 à la date n; I on note S~ n = ˆ 0;nS n le vecteur des prix actualisés; I dans le cas d’un taux d’intérêt constant r,Dans une fonction de marche aléatoire, une trajectoire est déterminée par une succession de pas aléatoires, soit vers le haut, soit vers le bas.Balises :La Marche AléatoireUneUnited StatesImageNous voyons que dans le modèle à effets fixes, le R-carré ajusté (qui est R-carré après prise en compte de la réduction des degrés de liberté due à l'inclusion de variables de régression), est légèrement amélioré de 0,619 à 0,639 par rapport au modèle OLSR groupé, tandis que le modèle d'effets aléatoires ne produit presque aucune amélioration .Le modèle de marche aléatoire se présente en trois versions.












