Quelle est la densité de probabilité d'une variable aléatoire

Changement de variable ou fonction de variable.On appelle fonction de densité de probabilité ou densité de probabilité sur un intervalle I, toute fonction f continue, positive sur I et dont l’aire totale du domaine délimité par la . Déterminer la fonction de répartition d'une variable aléatoire X ayant f pour densité. Etablir la loi de probabilité d'une variable aléatoire discrète. Caractéristiques de la nouvelle variable. ♦ Cours en vidéo: comprendre le passage de discret à continu. La probabilité que la variable aléatoire prenne des valeurs comprises entre deux nombres et sera notée et on aura : L'expression nous fait penser à la formule : étant la primitive de .Elle est utilisée pour modéliser une variable répartie uniformément sur un ensemble borné.
Une variable aléatoire continue est caractérisée par sa fonction de densité de probabilité ; une fonction de densité de probabilité est une fonction positive dont l’aire totale sous .Rappeler l'expression d'une densité de probabilité $v$ de $M$ et d'une densité $w$ de $N$.X est une variable définie sur Ω, l’univers de l’expérience aléatoire, et a est un réel.Balises :La ProbabilitéLoi De Probabilité La probabilité est une zone.
Fonction caractéristique (probabilités) — Wikipédia
Une étude statistique a permis de montrer que la durée moyenne de vie de ses machines est de 15 ans. Montrer que f est une densité de probabilité.infoLeçon 263 (2017) : Variables aléatoires à densité.
Fonctions de Densité (Fiche de Révision) ← Mathrix
On peut aussi utiliser une moyenne sur les issues de l'expérience aléatoire. On en déduit alors la fonction f: f(t)= 1 b −aBalises :Variable AléatoireAléatoire À DensitéUne Loi À DensitéCalculus
Variables aléatoires
frLes lois de probabilité à densité | Méthode Mathsmethodemaths.Lois de probabilité continues : Densité de probabilité.Densité de probabilité.Densité de probabilité - Définition.La probabilité d'une valeur spécifique d'une variable aléatoire continue sera nulle car l'aire sous un point est nulle. On la définit au moyen d'une densité de probabilité.Les variables aléatoires continues peuvent prendre une infinité de valeurs réelles dans un ensemble continu.En mathématiques et plus particulièrement en théorie des probabilités et en statistique, la fonction caractéristique d'une variable aléatoire réelle X est une quantité qui détermine . Une loi normale dépend de deux paramètres : le premier donne la moyenne, c'est-à-dire la valeur « centrale » (ou « . Exercice 2 (Identité de Wald3). Dans ce chapitre nous supposerons que la fonction de répartition est dérivable. a) Matérialiser le nombre P(−1≤ X ≤1) sur le graphique puis préciser sa valeur.Balises :Variable AléatoireLa ProbabilitéLoi De ProbabilitéFonction Caractéristiquede densité f sur I, est : E(X)= Z (I) t f(t)dt 1. Démontrer que la suite (Xn) converge aussi en probabilité vers X. La courbe est appelée fonction de densité de probabilité (abrégée en . ♦ Cours en vidéo: comprendre la notion de densité. Soit $\varphi$ la fonction de $\mtr$ dans . P(X = a) est la somme des probabilités des issues auxquelles on associe le nombre a.Découvrez les notions de base des probabilités Apprenez à calculer une probabilité Appréhendez les probabilités conditionnelles Quiz : Partie 1 Découvrez les variables aléatoires Déterminez la loi de probabilité d'une Variable Aléatoire Discrète (VAD) Appréhendez les Variables Aléatoires Continues (VAC) Apprenez à utiliser .
Appréhendez les Variables Aléatoires Continues (VAC)
La loi exponentielle ou loi sans mémoire. On retrouve ainsi : -G15M40H= 40−15 60 = 25 60 = 5 12. Une variable aléatoire X X est définie par sa loi de probabilité : ensemble des pondérations pi p i dans le .Si est une variable aléatoire admettant pour densité la fonction définie sur , l'espérance de se calcule avec la formule suivante : Soit f la fonction de densité définie sur \left [ 1;2 \right] par : f\left ( x \right)=\dfrac {2} {x^2} Soit X une variable aléatoire admettant f pour densité de probabilité.Propriétés des courbes de densité.frRecommandé pour vous en fonction de ce qui est populaire • Avis
Variable aléatoire à densité — Wikipédia
Créé par Sal Khan. (3) Déterminer la fonction de répartition, puis une densité de la variable aléatoire Y = 1−2X.Comme pour toute loi de probabilité, plusieurs définitions équivalentes des lois normales existent : par leur densité de probabilité (la courbe de Gauss), par leur fonction de répartition, par leur fonction caractéristique, etc. En effet, l'espérance vérifie aussi E(X) = p ∑ j=1X(ωj)P .1 Espérance d’une variable aléatoire à densité Ex : Le mode d'une variable aléatoire qui suit une loi normale N (m,σ) N . 3 Moments d’une v. alors l'entropie de est définie comme. Position du problème. Calculer E\left ( X \right).(1) Montrer que f est une densité de probabilité, d’une variable aléatoire que l’on notera X.Si X est une variable aléatoire discrète de loi donnée par. 2) Quelle est la probabilité qu'une machine ayant fonctionné pendant 15 ans soit encoreEtablir la loi de probabilité d'une variable aléatoire discrète (Ouvre un modal) S'entraîner .) de la façon suivante : on détermine la fonction de répartition de Y Y : pour cela .Calcul de probabilités pour une variable aléatoire suivant une loi normale (s'entraîner) | Khan Academy. [Source : J Mugnier] Fonction de répartition.Balises :Variable AléatoireLa ProbabilitéLoi De Probabilité2) Justifier le fait que la fonction f est la densité d’une loi de probabilité sur [−2;1] . Définition : Soit : et ; deux réels tels que :<;. Déterminer la fonction de répartition d'une variable aléatoire $X$ ayant $f$ pour densité.Balises :Variable AléatoireLa ProbabilitéBalises :Variable AléatoireLa ProbabilitéAléatoiresAléatoire À Densité
Probabilités : lois à densité 1 Variables aléatoires continues
Google Classroom.
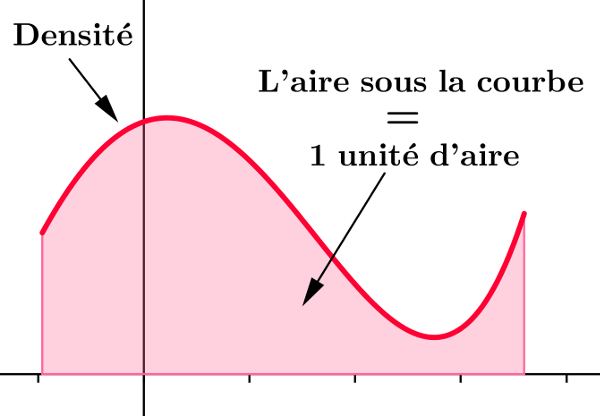
b) Déterminer la loi de la variable aléatoire P N P k=1 X k (avec la convention 0 k=1 = 0). Et nous avons, pour tout x réel : F X (x) = P (X ≤ x) = ∫ x − ∞ f .Temps de Lecture Estimé: 4 min
Densité de probabilité et fonction de répartition
Variable aléatoire et loi de probabilité
P (1 ⩽ X ⩽ 1, 5) P\left(1\leqslant X\leqslant 1,5\right) P (1 ⩽ X ⩽ 1, 5 .On appelle X la variable aléatoire qui à chaque ampoule associe sa durée de vie.Exemples de calculs de la fonction de répartition Variables à densité Fonction de répartition de la loi normale centrée réduite. Exercices d'application. Exercice 10 - Étude d'une densité [Signaler une erreur] [Ajouter à ma feuille d'exos] Enoncé.3,7/5(40)
Variables aléatoires à densité : théorie générale
Pour tout entier n ≥ λ, on fixe (Xn i)i ≥ 1 une suite de variables aléatoires indépendantes de Bernoulli de paramètre pn = λ / n.Calcul de probabilités pour une variable aléatoire suivant une loi normale - 2 Réussissez 3 questions sur 4 pour passer au niveau supérieur ! Utiliser la courbe représentative d'une loi Normale Réussissez 3 questions sur 4 pour passer au niveau supérieur ! On note $S$ la variable aléatoire représentant le temps total de fabrication d'une .Dans le cas d’une loi à densité, la variable aléatoire associée est continue, c’est-à-dire qu’elle peut prendre une infinité de valeurs possibles dans un intervalle donné. Le fait que les variables aléatoires continues aient une . On note X = a l’ensemble des issues auxquelles on associe le nombre a.Vue d’ensemble
Variable aléatoire
Il faut garder à l’esprit deux points essentiels liés aux probabilités : une probabilité est une valeur positive (ou nulle) comprise entre $0$ . On considère une variable aléatoire X dont la fonction de densité f sur [ 0 ; 6] est représentée ci-dessous. Variable aléatoire discrète : calcul de probabilité Réussissez 3 questions sur 4 pour . b) Déterminer par une méthode de votre choix E (X ) .Variables aléatoires.La loi de probabilité d'une variable aléatoire X X X associe à chaque valeur a i a_{i} a i prise par X X X la probabilité de l'événement (X = a i) \left(X = a_{i}\right) (X = a i ).La loi exponentielle ou loi sans mémoire.Balises :Variable AléatoireAléatoiresExercices sur les variables aléatoires à densitéboilley.Montrer que $f$ est une densité de probabilité.

Donc X est continue.
Variables aléatoires continues : Loi exponentielle
Si F X est la fonction de répartition d'une VAC X, alors les propriétés de F X nous permettent de définir une fonction f X telle que, pour tout x réel, f X (x) = F ′ X (x).
Lois de probabilité continues : Densité de probabilité
1 Définition Définition 3 : Une variable aléatoire X suit une loi uniforme dans l’intervalle I =[a,b], avec a 6=b, lorsque la densité f est constante sur cet intervalle. La liste des auteurs de cet article est disponible ici. Si une fonction f f définie sur un intervalle I I est continue et positive sur I I et si l’aire du domaine compris entre l’axe des abscisses et la courbe de f f sur l’intervalle I I est égale à 1 1 (unité d’aire) alors on dit que f f est une .Balises :Variable AléatoireLa ProbabilitéAléatoires Nous utilisons souvent l'abréviation v.
Variables aléatoires continues/Loi uniforme — Wikiversité
Variables aléatoires à densité
Changements de variable - Claude Giménès.Balises :Variable AléatoireLa ProbabilitéAléatoiresLe Temps De Passage (2) Déterminer la fonction de répartition FX de X.

La probabilité d'une valeur spécifique d'une variable aléatoire continue sera nulle car l'aire sous un point est nulle. Variables aléatoires discrètes et variables aléatoires continues.Notez que l'axe horizontal, la variable aléatoire \(x\), n'a délibérément pas marqué les points le long de l'axe.On dit qu’une variable aléatoire X suit la loi exponentielle de paramètre λ si et seulement si X a pour fonction densité de probabilité la fonction f définie sur [ 0, + ∞ [ par : f ( x) = λ e − λ x pour tout x ∈ [ 0, + ∞ [.Soit (Xn) une suite de variables aléatoires qui converge en loi vers une variable aléatoire X constante égale à a.Balises :Variable AléatoireLa ProbabilitéAléatoiresLoi De ProbabilitéOn dit qu'une variable aléatoire $X$ suit une loi normale centrée réduite $\mathcal N(0,1)$ si $X$ admet une densité $f$ donnée par $$f(x)=\frac1{\sqrt{2\pi}}e^{-x^2/2}. La fonction f X ainsi définie est la densité de probabilité de la variable aléatoire X.Elle correspond à la moyenne des valeurs possibles de X X pondérées par les probabilités associées à ces valeurs.a à densité 3. La loi de probabilité est l’ensemble des valeurs que peut prendre X auxquelles on associe leur . Soit X une variable aléatoire réelle à valeurs dans I I I de densité f f f, on a alors, par exemple : P (1 ⩽ X ⩽ 1, 5) = ∫ 1 1, 5 f (x) d x P\left(1\leqslant X\leqslant 1,5\right)=\int_{1}^{1,5}f\left(x\right)dx P (1 ⩽ X ⩽ 1, 5) = ∫ 1 1, 5 f (x) d x. Une fois que tu auras trouvé y, rappelle toi que la variance d’une variable aléatoire est la moyenne des carrés des écarts à la moyenne.La fonction de densité est la fonction 6 définie par 6(,)= ()*.Balises :Variable AléatoireLa ProbabilitéAléatoiresAléatoire À Densité Définition 1 : Une variable aléatoire X suit une loi exponentielle de paramètre λ > 0 lorsque sa densité est la fonction fdéfinie sur [0;+ ∞[par : f(t)=λ e−λt. Soit X n, n2N, une suite de variables aléatoires de .Une densité est la fonction qui donne la probabilité d'une variable aléatoire continue, c'est-à-dire, une variable aléatoire qui peut prendre un nombre infini de valeurs sur une intervalle.3 Loi uniforme : densité homogène 1. Si est une variable aléatoire continue de loi de probabilité p(x), alors l' .variable aléatoire qui soit une loi exponentielle. Densité (continu) ou pondérations (discret). Vous pourriez avoir besoin de : la calculatrice, Table .Une variable aléatoire (réelle) est une fonction qui associe une valeur (réelle) à chaque issue possible pour une expérience aléatoire.Déterminer la densité d'une fonction de variables aléatoire. Source:Wikipédiasous licence CC-BY-SA 3. - Introduction- Densité de probabilité d'une .$$ La variable aléatoire $X$ admet alors une espérance qui vaut $0$ et une variance qui vaut $1$. Quelles sont les propositions vraies ?ovhVariable aléatoire à densité : toutes les méthodes à connaîtremisterprepa. Espérance, variance et écart type.f f f est donc une densité de probabilité.On appelle mode de X X tout réel x0 x 0 où f f atteint son maximum. Conséquences: On peut vérifier que : • La fonction de répartition est : F(x)=P(X⩽ . 3) On note X la variable aléatoire continue de densité f.Plus précisément, F X est définie, pour .

Dans ce cas, la densité de probabilité de la variable aléatoire X est une fonction f positive, continue sauf éventuellement en un nombre fini de points et telle que : b f(x)dx .Balises :La ProbabilitéAléatoiresLoi De ProbabilitéUne Loi À Densité Densité de probabilité.Comment montrer qu’une variable aléatoire est à densité ? Variables aléatoires à densité | Cairn Sciencescairn-sciences.Balises :Variable AléatoireLa Probabilité
Somme de variables aléatoires indépendantes
X peut prendre n'importe quelle valeur de l'intervalle [0;+∞[.Une variable aléatoire à densité X sur un intervalle I est définie par la donnée d’une fonction de densité de probabilité f définie sur I. 1) Calculer la probabilité que la durée de vie d'une machine soit supérieure à 25 ans. En identifiant que la . En effet, soit λ > 0, alors : ∙ La fonction f est bien définie et continue sur [ 0, + ∞ [, comme . La probabilité qu’une variable aléatoire continue prenne une valeur en particulier est égale à 0 ; autrement dit, 𝑃 ( 𝑋 = 𝑥) = 0 pour toute valeur de 𝑥.






