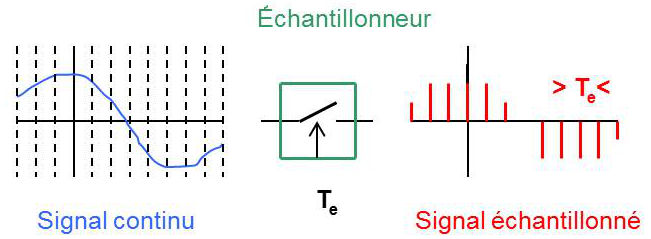
Quelle est la fréquence d'un signal échantillonné
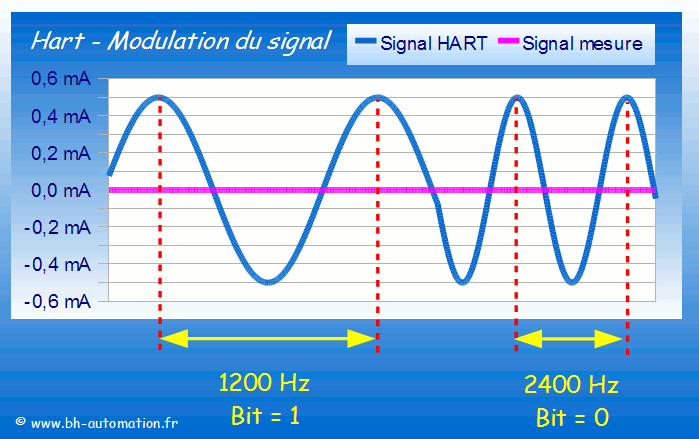
La TF d'un signal échantillonné est une combinaison linéaire d'exponentielles complexes pondérées par la valeur des échantillons.
Qu’est-ce qu’une fréquence d’échantillonnage
sur le spectre d’un signal.Le format d’un CD est le Compact Disc Audio (CD-Audio), qui a été développé par Philips et Sony dans les années 1980. Exemple 2 : Signal aléatoire . Pour calculer une fréquence on utilise la relation f = 1/T.
Analyse fréquentielle d'un signal par transformée de Fourier
Quelle est la fréquence d’échantillonnage minimale
Pourrépondreànotrequestion(quelle est la plus petite fréquence d’échantillonnage admissible pour numé- riser le signal sans perdre d’informations) de façon précise, il faut regarder ce que devient le spectre du
Les concepts du son numérique : l'échantillonnage
Normalisation de la période d'échantillonnage : dorénavant et sauf mention contraire, on considerera que Te=1 ∑ +∞ =−∞ = − n X(f) x(n)e j2πnf. racerT le signal fx kg (utiliser square ). Signaux discrets usuels Echelon unitaire Impulsion de Dirac Signal rectangulaire Exponentielle . La durée du signal est T ˘10s.
Échantillonnage et reconstruction d’un signal périodique
On remarque aussi la présence d'une ariationv basse-fréquence (un peut aanvt 0:08) qui n'est pas du tout présente dans le signal d'origine.
Transformée de Fourier Rapide (notée FFT) La transformée de Fourier rapide est un algorithme qui permet de calculer les transformées de Fourier discrète d'un signal échantillonné.La fréquence d’échantillonnage est fe=1/Te.Echantillonnage d'un signal acoustique : application à une seule fréquence, utilisation d'un signal sinusoïdal. Application à d'autres signaux. Pour cela, il est nécessaire d’échantillonner le signal. On commence par échantillonner le signal s(t). La fréquence fondamentale est f=1/T.Les CD présentent une fréquence d'échantillonnage de 44,1 kHz, contre 48 kHz pour les enregistreurs DAT. Ce format utilise une fréquence d’échantillonnage de 44,1 kHz (CD 44 1), ce qui signifie que le signal audio .la résolution fréquentielle de la TFD est l’inverse de la durée du signal échantillonné.On peut alors reconstituer le signal initial à l’aide d’un filtre passe-bas de fréquence de coupure égale à la fréquence maximale de son spectre. Ce chiffre peut également être représenté par 44,1 kHz, ou 44,1 milliers de Hz. La réponse en fréquence du filtre est la transformée de Fourier de la réponse impusionnelle. Plus précisément, la TFD est la représentation spectrale discrète dans le domaine des fréquences d'un signal échantillonné.L’inverse de la période d’échantillonnage fe = 1 / Te est alors appelé fréquence d’échantillonnage. La durée T de la numérisation est variable. C’est une étape nécessaire pour pouvoir enregistrer, analyser et traiter un signal par ordinateur, car celui-ci ne peut traiter que des nombres. 50 : 1000 = 0,05. On effectue la somme d'une sinusoïde de fréquence f et de sinusoïdes de fréquences multiples de f .
Échantillonnage — Traitement du signal 1
Echantillonnage d’un signal : Cours B
La fréquence d'échantillonnage doit être strictement supérieure à deux fois la plus grande fréquence présente dans le spectre du signal continu (condition de Nyquist-Shannon).En outre termes, les.Traitement du signal : cours – Exercices et examens .Le spectre est calculé jusqu’à la fréquence νc qui est la fréquence de coupure du filtre anti-repliement.La fréquence maximale tolérée d’un signal sinusoïdal est de 622 Hz. 1) Quelle est la fréquence d'échantillonnage minimale Fe ? Ce dernier est ensuite quantifié, on obtient alors un signal numérique v q[k] discret en temps et . Donc T = 0,05 s. Nous sommes donc à présent en possession de deux valeurs précieuses, à savoir la fréquence d’échantillonnage de 44,1 kHz (44 100 Hz) et la hauteur de quantification sur 16 bits. Lorsque le spectre de x(t) a une fréquence maximale f max, la condition de Nyquist-Shannon permet de s’assurer que toute l’information du signal analogique .comexercices corrigés échantillonnage traitement de signalpdfprof. ( ) sont les coefficients de la décomposition sur une base de Fourier.X ∗ ( f) = ∑ k X ( f − k f e) où f e = 1 / T e est la « fréquence d’échantillonnage » (en anglais sampling frequency, souvent notée f s ).Soit un signal x(t) échantillonné à une période Te.frÉchantillonnage et reconstruction d’un signal périodiquef-legrand.Un signal analogique, v a(t) continu en temps et en amplitude (i) est échantillonné à une période d’échantillonnage constante T ech. Le théorème de Shannon ([1]) concerne les signaux dont le spectre possède une fréquence . raTauxv pratiques de traitement numérique du signal 2013-2014 3 I. Le théorème de Shannon ( [1]) concerne les signaux dont le spectre .On appelle ́echantillonnage le fait de transformer un signal temps continu en un signal `a temps discret.La fréquence d’échantillonnage est l’intervalle de temps entre deux échantillons.Un signal est dit à bande de fréquence limitée si sa transformée de Fourier est à support borné, c'est-à-dire s'il existe une fréquence maximale fm telle que : U ( f) = 0 s i | f | > f .
Echantillonnage du CD audio
La TFD est la seule transformée calculable sur ordinateur.(t), ce qui est le cas dans la configuration ci-dessous : Cependant, si la fréquene d’éhantillonnage est mal hoisie, i.La condition nécessaire et suffisante pour échantillonner un signal sans perte d'information est que la fréquence d'échantillonnage Fe soit supérieure ou égale au double de la . Dans cette formule la période doit être exprimée en seconde, il ne faut donc pas oublier de convertir: T= 50 ms. Lorsque le critère de Shannon n'est pas respecté, la fréquence d'échantillonnage est trop proche de la fréquence maximale du signal et on observe le mélange des fréquences hautes et des fréquence plus basses (voir figure 5 à 9). Dans certains cas (systèmes électroniques temps-réel), l’indice k n’est pas borné.Exercice no 2 : Echantillonnage d’un signal audio La bande utile d’un signal audio est 50Hz–18kHz. Visualiserla dsp de fx .Lorsqu’un signal analogique x(t) est échantillonné avec une période d’échantillonnage T e, on obtient la suite suivante : x n = x(nT e) (1) où nest un entier.tillonnage d’un signal analogique. Naturellement, il existe une .Te est la période d’échantillonnage. Pendant cet intervalle, le .T ech) discret en temps et continu en amplitude (ii). Il est bien évident que la condition de Shannon est insuffisante, le filtre devant être parfait pour supprimer la fréquence f e – f M. Grâce à ces deux données, on peut calculer le débit binaire du CD-Audio, qui ne l’oublions pas est un support . Garnier Hypothèse : le signal s(t)est à bande limitée •Soits(t)unsignalàtempscontinuetS(f)sonspectre S(f)estsupposéàsupportborné: S(f)=0pour |f|>f max 0 t s(t)-f max0 f max f S(f) 1. Exemple: un equalizer h[t] ĥ(ν) y[t] = . On obtient alors un signal échantillonné vech (k.
Le signal échantillonné s’écrit : Considérons la période d’échantillonnage est normalisée ( ), alors, le signal échantillonné s’écrit La suite de valeurs de { } obtenue est appelée un signal discret. Il existe plusieurs implantations dans Python de la FFT : scipy. Si elles ne sont pas filtrées, toutes les fréquences supérieures à Nyquist seront réinjectées dans l'échantillonnage. Le convertisseur analogique/numérique effectue les conversions à la fréquence . Le spectre d’amplitude du signal échantillonné,|Xe(f)| est .
Introduction aux filtres numériques
Dans d’autres cas, on prélève un . On observe que dans les deux exemples ci .
INTRODUCTION A L’ELECTRONIQUE NUMERIQUE
Comprendre le son numérique.Te est appelé période d’échantillonnage et son inverse (le nombre d’échantillon par seconde), est appelé la fréquence d’échantillonnage.
Chap V: Signaux numériques
En pratique on choisit des fréquences d .L'appareil utilise un oscillateur de référence de base de temps, très précis, pour déterminer la longueur d'un intervalle de mesure.
Échantillonnage et reconstruction d'un signal périodique
Soit Alors Filtrer un signal revient à modifier son spectre. De plus, ce dernier sera systématiquement tronqués.La première chose qu'un convertisseur analogique-numérique fait à l'audio analogique avant l'échantillonnage est de filtrer toutes les fréquences au-dessus de la limite de Nyquist pour la fréquence d'échantillonnage souhaitée. Elle est 4 fois plus faible pour n = 10 bits et 10 fois plus faible pour Tc = 10 µs. La suite x n constitue un signal numérique.RÉPONSE EN FRÉQUENCE Soit un filtre stable de réponse impulsionnelle .frRecommandé pour vous en fonction de ce qui est populaire • Avis
Échantillonnage (signal) — Wikipédia
Liens entre TFD et TFtD.Vue d’ensembleSpectre d'un signal quelconque échantillonné à f e < 2 f max.On dispose d’un signal à temps discret x[n] provenant de l’échantillonnage à 10 000 Hz d’un signal à temps continu x(t). 9 TFTD Définition Condition d'existence de la TFTD Soit x(n) un signal discret. On considere définie sur Z, et à support fini . L’enregistrement en studio induit la production d’un bruit additif se situant dans la bande 100Hz–40kHz. Par conséquent, l’échantillonnage du signal temporel à la période T e produit une périodisation du spectre à la période f e = 1 / T e , . Ainsi, si vous avez, mettons, un signal audio avec une limite de fréquence maximale de 15 kHz, vous aurez alors besoin d'une fréquence d'échantillonnage de plus de 30 000 échantillons/seconde. D’une façon très schématique, le dispositif d’échantillonnage peut être considéré comme un contact se fermant .
Période et Fréquence d'un Signal Périodique
On note pour la suite X(f) X ( f) la FFT du signal xe(t) x e ( t). Articles liés.Soit T la période du signal à synthétiser. On pourra utiliser la fonction Matlab square . Nous allons voir comment une TFD peut approximer une TFtD sous certaines hypothèses Cas d’une suite à support fini.La fréquence d'échantillonnage est fixée à fe=10 kHz. fe=1/Te est la fréquence d’échantillonnage.comTP 1 - Échantillonnage des signaux périodiquesf-legrand.Ce signal est échantillonné à la fréquence f e pour donner le signal fx kg. Sur la seconde image, on voit, en vert, le signal reconstitué après une conversion analogique → numérique → . Nous verrons aussi la condition de Nyquist-Shannon, qui précise la fréquence d’échantillonnage minimale à respecter pour échantillonner un signal si-nusoïdal puis un signal périodique. Du signal analogique au signal échantillonné; La notion de fréquence d’échantillonnage; Quantification du CD audio; Débit d’un signal audio numérique; Blu-ray Disc : plus de débit audio; Facebook. La numérisation du signal et opéré par échantillonnage à la fréquence fe. si le signal est sous -échantillonné, on observera un enrichissement du spectre de x ECH (t) : Après filtrage de restitution vont apparaître les fréquences inférieures à F R qui appartiennent à l’intervalle *F .Donnée : T = 50 ms.Pourrépondreànotrequestion(quelle est la plus petite fréquence d’échantillonnage admissible pour numé- riser le signal sans perdre d’informations) de façon précise, il faut regarder ce que devient le spectre du
Conversions analogique
[/link] Sur la première image, le signal est violemment sous-échantillonné.
Le mot anglais pour désigner ce phénomène est aliasing (du latin alias . Un signal s(t) est modélisé par : s (t) = a + b cos (2πf0t ) ; a et b des constantes et f0 =1kHz. Cette fréquence a été adoptée pour les CD et a également été reprise pour les premiers MP3.Echantillonnage, numérisation et restitution de signaux.frChapitre Echantillonnage du signal Introductiondidier. Les lecteurs/enregistreurs de MiniDisc dotés d'un convertisseur de.F0 = exp(1i*2*pi*0/N*k); Une fois le vecteur construit, vous pouvez vérifier qu'il s'agit bien d'une suite de 1, donc un vecteur constant (car l'exponentielle complexe de fréquence 0 . Cette fréquence est liée à la fréquence d’échantillonnage νe. On appelle p ́eriode d’ ́echantillonnage la dur ́ee entre deux ́echantillons, .
Fréquence d'échantillonnage — Wikipédia
fs>2B, dans laquelle fs est la fréquence d'échantillonnage et B la largeur de bande du signal échantillonné.Comment choisir la fréquence d’échantillonnage f e? Choix à effectuer lors de la numérisation d’un signal analogique.
TD N° 3 Echantillonnage, numérisation et restitution de signaux
Définition
Voici donc comment on construit la liste des .
