Qu'est-ce que le marquage d'un réseau de petri

Avant d'aborder cette écriture, voici quelques définitions élémentaires.Eléments constitutifs d'un réseau de PETRI dans sa description graphique.L’ensemble des jetons dans les places représente le marquage du réseau de Petri et un marquage est associé à un état du système. Réponse : La transition T 1 est quasi-vivante, non vivante et T 2 est vivante, et donc quasi-vivante.
Marquage-piquetage : tout ce que vous devez savoir
Cours de Réseaux de Petri f20 / 46 2.
INTRODUCTION AUX RƒSEAUX DE PETRI
(Source de TD1 et ses corrigés : M. Tracer alors ce que l’on appelle un « graphe de marquage » : un graphe où les sommets sont les marquages atteints et les arcs, les transitions qui permettent de .MOTS-CLÉS: régulation du trafic, Réseau de Petri hybride, système non linéaire . Un r´eseau de Petri g´en´eralis´e est un r´eseau dans . De plus, un réseau de Petri interprété peut être temporisé.Les réseaux de Petri : Corrigé de TD1. J.Ce qui est parfaitement imagé.

Dé nition 2 (Marquage) Étant donné un éserau de Petri N= (P;T), un marquage m de Nest une fonction m: P !N qui associe à chaque place p2P du éserau m(p) jetons.Le marquage à un instant donné définit l'état du RdP, ou plus précisément l'état du système décrit par le RdP.pourra dire qu’un réseau est structurellement borné s’il est borné pour tout marquage initial fini.La quantité (p) est appelé marquage (initial) de p.Une place d'un réseau de Petri est dite k-bornée si elle ne contient pas plus de jetons dans l'ensemble des marquages accessibles, y compris le marquage initial. t1 0 t1 ω t2 Exemple 25 Deux graphes de couverture identiques mais le comportement des réseaux est nettement différent. M(p) = nombre de marques (jetons) contenues dans la place p .Définition : Un état est un doublet où : - M est une application de marquage, assignant à chaque place du réseau un certain nombre de marques (∀p∈P, M(p)≥0); - I est une application de temps d'indisponibilité, assignant à chaque marque k dans la place p un temps T. Ce dernier permet aux organisations de livrer des paquets clients dans l’ordre, d’un point à l’autre, sur Internet, sans subir de perte de paquets. Référence de fonctionnement de tout réseau de Petri.Unréseau marqué est le couple N = (R; ) formé de : un réseau R et une application (fonction totale) : P ! IN.Selon le cas, il y aura compilation pour une exécution en code machine, ou implantation sous la forme d’une base de données, le réseau de Petri sera alors interprété par un programme dit programme joueur, chargé de suivre l’évolution du marquage à partir du marquage initial. De la même façon, si pour tout marquage initial, le réseau est vivant, on dira que le réseau est structurellement vivant.
TD 9: Loi de Little et réseaux de Pétri
Réseaux de Petri
Toutes les infos
1 (Équation d’état).Dans le cas général, un réseau FIFO ne peut pas être transformé en RdP ordinaire.Donc Le modèle des réseaux de Pétri est un outil graphique de modélisation et d'analyse des systèmes parfaitement adapté à l'étude des structures de contrôle. La convention graphique veut que l'on représente un marquage men représentant m(p) jetons sous la forme de cercle noirs dans chaque place pdu réseau. 3 Etude des performances d’un centre de location de pédalos et bateaux Un centre de location est dirigé par 2 gérants. M est le marquage initial M : P N.Jeton: indique le marquage de chaque place. Réseau interprété: Dans un RDPS, lorsqu'on décide d'analyser les évolutions du marquage en tenant compte, pour franchissements, uniquement des évènements externes au réseau, donc de la validation ou pas des prédicats attachés aux transitions, on dit de ce réseau qu'il est interprété.comLes réseaux de Petri : Corrigé de TD1 - Academia.État d'un réseau de Petri p-temporel.Définition 1. Soit (R, m 0) un réseau de Petri et m f ∈ N P un mar-quage.
Les réseaux de Petri : Corrigé de TD1
C'est un graphe d'événements.Un réseau de Petri se représente par un graphe biparti (composé de deux types de nœuds et dont aucun arc ne relie deux nœuds de même type) orienté (composé d'arc(s) ayant un sens) reliant des places et des . Les intervalles de tir associés aux transitions du réseau dans un état différent la plupart du temps des intervalles initiaux.
Introduction aux Réseaux de Petri
comRecommandé pour vous en fonction de ce qui est populaire • Avis
Chapitre 4 LES RESEAUX DE PETRI
Ce module s’appuie sur MOCA-RP (pour MOnte-CArlo – Réseaux de Petri), propriété de TotalEnergies : un moteur de calculs ultra rapide basé, comme son nom l’indique, sur la simulation de Monte-Carlo et .Comment caractériser les réseaux M-bornés en terme de marquages accessibles? 2. Elle dénote le nombre de jetons présents dans la place p. (p) est lemarquagede la place p, on dit aussi lenombre de .
(CEG4561/CSI4541
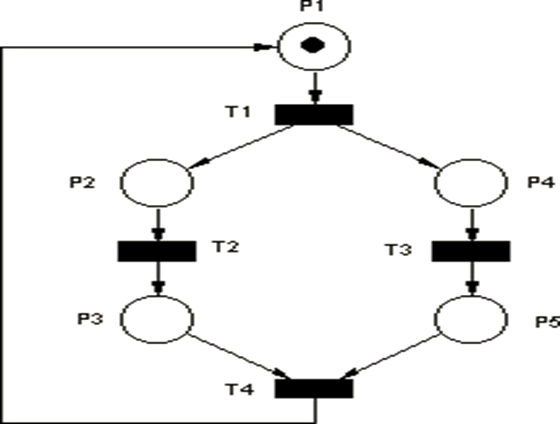
Montrer que si l’on retire la contrainte de positivité du marquage, alors on peut résoudre le problème de l’accessibilité en temps .Un RdP est graphe d'événement si chaque place n'a qu'une transition en amont et une en aval.Enoncé : Dans le réseau suivant, indiquer la vivacité de T 1 et T 2.
Les réseaux de Petri : définitions, propriétés et analyse
Un graphe orienté est fortement connexe s'il existe, pour tout couple de sommet .
Réseaux de Petri
Graphe de marquages et ensembles d’états dans la synthèse de supervision 2. Quel est sa complexité? 3.Un problème de réseau téléphonique, Internet, postal ? Alertez l’Arcep ! - 07/12/2023. Les réseaux de Petri : Corrigé de TD1 (Source de TD1 et ses corrigés : M.L’état d’un réseau de Petri t-temporel est défini par une paire , telle que : est une application qui associe à chaque transition du réseau un intervalle de temps pendant lequel elle est franchissable.8 Chapitre 2 : Introduction au RdP Réseau de Petri à arcs inhibiteurs Un arc inhibiteur est un arc orienté qui par d’une place P pour aboutir à une transition t. Le marquage du r ́eseau est constitu ́e de toutes les marques pr ́esent ́ees dans le r ́eseau `a un instant donn ́e. De manière générale, la congestion conduit à la .que les perspectives qu’ouvre ce travail. Les transitions (rectangles) décrivent les événements qui surviennent dans le .un vecteur (dit de marquage, ou de franchissement). Ce n’est donc pas le jeton . Cet accroissement du nombre de voies de circulation n’est cependant pas suffisant, ce qui implique l’apparition de phénomènes de congestion et de files d’attente, et dans le pire des cas, provoquent des accidents.Le graphe de marquages (GM) d’un réseau de Petri (RdP) est un automate à états finis de manipulation formelle facile (Dideban, 2007; Ferrier&Boimond, 2013) et défini comme . Download Free PDF. L’Autorité de régulation des communications électroniques et des postes .Un réseau de Petri interprété inclut, dans sa définition, la description de la relation entre partie commande et partie opérative.Représenter le fonctionnement de ce dernier RDP par un réseau de Petri coloré dont on précisera la signification des couleurs et des fonctions associées. On représente graphiquement les places par des cercles contenant des . t1,t2 1,0 C t1 ω,ω Analyser .

A Préliminaires Règle de fonctionnement . T est la durée qui reste à la marque k pour terminer son temps de séjour . t σr une suite de r transitions de T.4 Analyse de réseaux de Petri.Un réseau de Pétri est dit M-borné si le nombre de jetons dans chaque place ne peut dépasser M. 05/11/19 Blocage Un blocage (ou état-puits) est un marquage tel .En déduire un algorithme pour déterminer si un réseau de Pétri est M-borné. Ce centre contient un parc de 10 pédalos et de 5 bateaux.Un r ́eseau de Petri ordinaire est un r ́eseau dont le graphe sous-jacent est un 1-graphe.Dans ce type de réseau, les compteurs sont associés aux transitions (en effet, puisqu’ils sont limitatifs, un jeton à la fois transite par la transition qui gère le compteur temporel, .

Td corrigé Les réseaux de Petri : Corrigé de TD1 pdftdcorrige.Un blocage correspond à un marquage du réseau de Petri pour lequel plus aucune transition n'est franchissable. L’état d’un réseau de Petri p-temporel est défini par une paire =, telle que : est le marquage du réseau ; est une application temps de séjour qui associe à chaque jeton ; présent dans la place pi un nombre réel correspondant à l’âge de ce jeton, c’est-à-dire le temps écoulé .Formellement, un réseau de Petri est un triplet N = {P, T, F}, où P est un ensemble de places, T un ensemble de transitions, et F un ensemble d’arcs orientés. Au plan structurel, alors qu'un graphe de fluence (la modélisation graphique pour machines .Dans le cas général, le problème de l’accessibilité est EXPSPACE-di cile.2 Validation des transitions : Si une transition Ti est validée pour un marquage initial M0, il faut que : ∀ Pj ∈ P, M(Pj) ≥ E(Pj, Ti) Soit |M0| ≥ E(P, Ti) En comparant .2 Franchissabilité Proposition 1: Pour qu'une transition soit franchissable, il faut et il suffit que l'on Soit σ = t σ1 t σ2. On représentera la structure d’un réseau de Petri soit sous la forme . Donner un semi-algorithme pour le résoudre.Le marquage dit initial décrit l’état initial du système modélisé. R est un réseau de Petri.Petri permet de modéliser le comportement de systèmes dynamiques complexes par réseaux de Petri stochastiques à prédicats et assertions.
R seaux de Petri
La gure 2 repré-sente le .L’opération de Marquage-Piquetage est l’une des premières opérations à réaliser dans un chantier, le code couleur (disponible ci-dessous) doit être respecté car il répond à la norme NF P 98-332. Par exemple, dans le cas de la lampe, le . Deuxième partie : définitions et notations . Une couleur sera ainsi attribuée pour chaque type de réseau détecté. Il se matérialise par la localisation au sol des réseaux enterrés grâce à des tracés colorés propre à chacun.Un réseau de Petri est vivant pour M0 si toutes ses transitions sont vivantes pour M0.comExercices corriges Les réseaux de Petri : Corrigé de TD1 pdfexocorriges.Tracer alors ce que l’on appelle un « graphe de marquage » : un graphe où les sommets sont les marquages atteints et les arcs, les transitions qui permettent de passer d’un . À chaque transition du réseau autonome est associé un prédicat, fonction des mesures effectuées sur le processus commandé.
Couleur
Réseau de Petri T-temporel — Wikipédia
La séquence t1t2t2 étiquette bien un chemin du graphe de couverture partant de Mo et pourtant la séquence n’est pas tirable depuis Mo. Structure G = (X, U) X: ens . Chaque place va contenir un nombre entier de jetons (ou marques) pour mod ́eliser la dynamique du syst`eme.Gestion du trafic point à point : La gestion d'un réseau est essentielle, quelle que soit la manière dont le trafic est acheminé, que ce soit de bout en bout, de nœud à nœud ou de point à point.1 Analyse par le graphe des marquages Pour un réseau borné, partant du marquage initial, on peut générer les mar-quages de façon exhaustive, à condition que ce nombre . Le marquage initial est noté M O On peutlimiter le marquage des places à 1 ou à un entier k. Il est également impératif d’indiquer la profondeur du . Christian Attiogbé (Janvier 2020) Modélisation avec les Réseaux de Petri 17/47 Les bases Marquage des places (repos) = 1 (production) = 0 .Le marquage-piquetage est une étape obligatoire avant tout commencement de travaux afin de préserver les réseaux souterrains de tout endommagement et ainsi la sécurité des intervenants. Elle est dite sûre si elle est 1-bornée et bornée si elle est k-bornée pour un entier .Marquage accessible.eduRecommandé pour vous en fonction de ce qui est populaire • Avis
Réseau de Petri
Un réseau de Petri de haut niveau est un réseau coloré et hiérarchique.