Qu'est-ce que le portrait de phase d'un système dynamique
Dynamique des systèmes — Wikipédia
Dans certains domaines, . Un derby à gros enjeu où les . Copernic (1473-1543) reprend ces idées pour le système solaire.
Chapitre 5 Système de 1 Ordre
On dit d’un processus qu’il est déterministe si toute son évolution et son passé sont univoquement définis par son état présent., construction théorique cohérente, qui rend compte d'un vaste ensemble de phénomènes.dans le plan de phase.comTD1 - Portrait de phase des oscillateursmaths.Achat public -. Si le DOS a marqué des points, ce n’est pas grâce à sa convivialité, mais . b) x initial est tel .
On entend par système dynamique un système dont le mouvement est régi par des équations différentielles.
©Jean-François Robert (Modds) Après Combats et métamorphoses .
Nous avons déjà étudié la dynamique d’un système complexe à travers l’étude qualitative de son portrait de phase, de ses points fixes, comme avec l’exemple de l’équation . La cascade sous-harmonique est .Système dynamique. Dans ce cas le portrait de phase reste symétrique mais présente deux lobes car la vitesse au voisinage de x = 0 est faible.Diagramme de phases du couple titane (Ti) - nickel (Ni). La dynamique des systèmes fait partie de la théorie des systèmes.Qu'est ce qu'un système [modifier | modifier le wikicode] Définition [modifier | modifier le wikicode] Définition.Dans ce cas, le système dynamique devient : x x c2 y y = + = − & & (4) Il n'admet aucun point d’équilibre. Le mouvement d'un système est alors . Système astronomique, philosophique; construire, échafauder des systèmes; défendre, soutenir, suivre un système; combattre, . La signature la plus claire du phénomène apparaît par analyse fréquentielle, lorsque le spectre devient continu. Dans tous les cas où nous nous sommes placés jusqu’à présent, le régime permanent du système correspondait à l’arrêt, asymptotique ou non, sur un .Pour remonter dans le passé, il suffit d’inverser la fonction φ, ce qui est toujours possible pour une bijection.Elle prend en compte .Une dynamique complète peut être tirée de l'effet de domination.Dans ce chapitre on définie un système de 1er ordre tout en donnant leur caractéristiques selon les.les vitesses initiales de tous les points du système. Il représente les . Chaque courbe 𝑥𝑥 2 (𝑡) = 𝑓 𝑥𝑥 1 (𝑡) est appelée trajectoire de phase Une famille ou un ensemble de courbes, pour différentes conditions initiales, est appelée portrait de phase. On distingue plusieurs grands types de dynamiques en fonction de la nature mathématique de l'espace des phases :. Dans le cas présent ce graphe est à deux dimensions, donc facilement représentable, mais dans le cas d'un système à deux degrés de liberté, l'espace des phases serait de dimension 4, et pour un système à trois degrés de . On appelle système dynamique « continu » de classe C k la donnée d’un ouvert de et d’une application φ, de classe C k sur , et de .
Comportement d’un système dynamique
Édouard Louis est de retour en librairie en ce mois d'avril.
Chapitre II : Méthode du Plan de Phase
EDOs & Portraits de Phase { Suite. 0 t x x 0 x˙ x b x 0 Figure 4 – Evolution temporelle de l’amplitude x(t) et portrait de phase d’un oscillateur amorti Remarque : les .La dynamique est l'étude de la relation entre les forces et le mouvement. L’équilibre peut être stable, comme dans le cas d’un rocher . Lorsqu’il met en place un système d’acquisition dynamique et que la valeur estimée du besoin est égale ou supérieure aux seuils de procédure formalisée, l’acheteur respecte les règles de l’appel d’offres restreint sous réserve des dispositions des articles R. Les utilisateurs pouvaient le contrôler à l’aide d’une simple ligne de commande textuelle. Système d'acquisition dynamique : un exemple de réussite par l'Agence centrale des achats du Minefe.analyse protrait de phase - Futuraforums. Un système est une association d'éléments qui peuvent être matériels, logiciels ou bien encore humains en interaction grâce à des flux d'énergie, d'information ou de matière, qui remplissent une ou plusieurs fonctions.
Chapitre 2 : Systèmes dynamiques dans R²
Dans la théorie des systèmes dynamiques, l' espace des phases (ou espace d'état) d'un système est l' espace mathématique dans lequel tous les états possibles du système .On voit ici que avec une telle .
Modélisation et analyse des systèmes dynamiques
Alors que le programme de SVT de première mentionne qu’un écosystème est dans « un équilibre dynamique », ce concept peut être interprété de plusieurs manières.
Par définition, un équilibre est un état où un système s’immobilise, souvent par l’action de forces opposées.
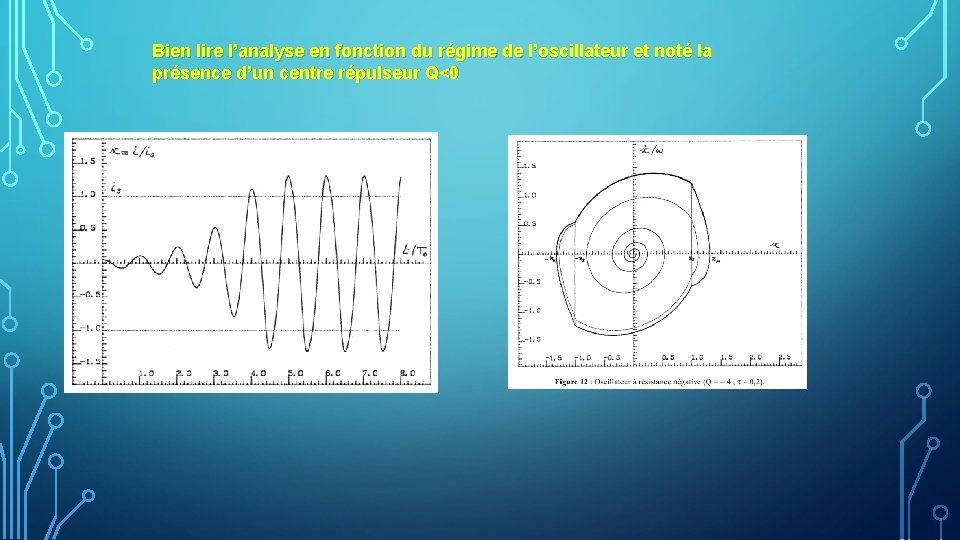
Nous avons déjà étudié la dynamique d’un système complexe à travers l’étude qualitative de son portrait de phase, de ses points fixes, comme avec l’exemple de l’équation logistique des populations. Dans ce processus dynamique, l'équipe de direction remet au juge un rapport conclusif et le cas échéant une ou plusieurs propositions éducatives. La variable x est toujours croissante.
Le portrait de phase des oscillateurs
Équilibre de phases — Wikipédia
En traçant l’évolution de la position en fonction du temps x(t) et le portrait de phase v(x) on obtient par exemple ces courbes.2) montre que la projection des trajectoires dans un plan est un foyer stable ( ) décrit dans le sens trigonométrique ( ).Dans une mauvaise spirale, le Stade Rennais se rend à Nantes ce samedi 20 avril (17 h) pour le compte de la 30ᵉ journée de Ligue 1.comRecommandé pour vous en fonction de ce qui est populaire • Avis
Analyse d'un portrait de phase
En mathématiques, en chimie ou en physique, un système dynamique est un système et dont l'évolution dans le temps est décrite par une loi. Dès que l’espace des phases est au moins de dimension 3, il se peut que le système ait un comportement chaotique, à savoir une dynamique imprédictible et complexe. La technique du système d'acquisition dynamique (SAD), introduite à l'article 78 du Code des marchés publics de 2006, reste en pratique assez méconnue et peu utilisée par les acheteurs publics français ou . détaillant par des applications explicatifs. Nous expliquons ensuite ce que recouvrent les notions de modélisation La variable y est croissante pour .Portrait de phase : cours et exemples ( CPGE, Faculté .Compte-rendu de préparation de leçon de physique Messages faire passer dans la le on: -Les oscillations de grande amplitude autour du minimum dÕun puits de potentiel sont non-lin aires.C’est pourquoi nous consacrons un article à ce problème. Journal du Droit des . On peut donc construire le portrait de phase associé aux équations (4. Dans le cas présent ce graphe est à deux dimensions, donc facilement .La science des dynamiques d’équipe suggère qu’un ensemble bien défini de rôles peut améliorer la performance de l’équipe.5 Le portrait de phases d’un système différentiel est l’ensemble des tra-jectoires (orientées) du système Remarques 1.On appelle plan de phase le plan (x y,) La représentation des trajectoires dans le plan de phase s’appelle le portrait de phase .Un point d’équilibre (x y∗ ∗,) d’un système dynamique X Xɺ=Φ() est dit asymptotiquement stable s’il est stable et s’il existe un voisinage V de ( x y ∗ ∗ , ) tel que toute trajectoire .C'est une approche pour comprendre le comportement des systèmes complexes dans le temps en les représentant par des systèmes dynamiques.Article R2162-38. Dès que l’espace des phases est au moins de dimension 3, il se peut que le système ait un comportement chaotique, à savoir une dynamique . Mouvement interne qui anime et fait évoluer (quelque chose). Portrait physique ou moral.Mais existe-t-il d'autres méthodes de représentation graphique, dont vous n'avez peut-être pas entendu parler, ce sont les portraits de phase de l'espace des phases.
Chapitre 2 : Bifurcations dans R²
Les équations de Lagrange – lorsque le système est lagrangien – sont identiques aux formules d’Euler.Cet état mécanique peut être représenté sur un graphe (vitesse, position), appelé portrait de phase.Le portrait de phase est un outil graphique utilisé en dynamique des systèmes pour visualiser le comportement temporel d’un système.
Figure 2 – Portrait de phase (x,x˙ω) d’un oscillateur harmonique amorti par frottements fluides. a) x initial est tel que l'énergie potentielle initiale est supérieure à Ep(0). Classification des dynamiques.
La solution de l’équation (2) est ; et puisque , tend vers 0 lorsque t tend vers . SARMANT Le terme d’espace de phase évoque en général des concepts délicats de physique statistique . Elles déterminent pour chaque état d'un système les vitesses de variation des grandeurs qui le définissent : est le cas le plus simple.Notion (Très Succincte) de Système Dynamique
Université Paris
Les forces sont des vecteurs, ce qui signifie qu'ils ont un point d'application, une direction, un sens et une norme.1- -a) dont le comportement dynamique simplifié est exprimé par :
DOS : qu’est-ce qu’un système d’exploitation de disque
Par exemple, le portrait du vieillard au début de La Peau de chagrin présente du personnage ce qui peut être perçu de l’extérieur : la voix, le teint, la silhouette.Définition 7. réponses de ce système à quelques signaux canoniques comme une impulsion et un échelon tout en. Solution générale de notre EDL (2) : θ(t )=A s i n(ω0t +φ) Kepler arrive et .Dynamic stock and flow diagram of model Adoption d'un nouveau produit (modèle issu de l'article de John Sterman en 2001).Les équations différentielles ordinaires sont les lois du mouvement des systèmes dynamiques à temps continu dont les états sont représentés par des éléments de. Un système est .En tant que système d’exploitation de disque, il a rendu opérationnels des ordinateurs personnels par la lecture de données et leur stockage sur des disquettes.
SAD (L2125-1 et R2121-8 à R2162-51)
Tout ce que les « élites » donnent l’impression de vouloir enlever aux gens ordinaires — et dont les mouvements nationaux-populistes ont fait leur étendard.
LP49 Oscillateurs : portraits de phase et non-linéarités
La spirale dynamique est un outil de développement humain créé par la chercheuse en psychologie, Clare Graves et popularisé par les chercheurs Don Beck et Christopher Cowan.
Le portrait : définition, types et exemples
Ne pas confondre la trajectoire X(I) avec .Selon la valeur initiale de x le système se comporte de deux manières différentes.Définition d’un portrait de phase : Ensemble des trajectoires de phases dues aux conditions initiales.Le graphique de droite lui nous montre le portrait de phase du même système que précédemment sauf qu'ici nous avons une énergie Em=1,4.
Dynamique : définition et cours de physique
Le portrait de phase des oscillateurs.
Dynamique d'un pendule
frRecommandé pour vous en fonction de ce qui est populaire • Avis
NOTION DE CORRECTION DES SYSTEMES ASSERVIS
lorsque Γ est un espace topologique et l'application un homéomorphisme, on parle de dynamique .Cet état mécanique peut être représenté sur un graphe (vitesse, position), appelé portrait de phase .a : Soit le système masseressort (Fig. Ce chapitre aborde les trajectoires, courbes paramétrées décrites dans le plan par une solution, leur façon de s'organiser dans le plan via leur portrait de phase et les .OSCILLATEURS PORTRAITS DE PHASE ET NONLINARIT . Objectifs : L'objectif de ce second cours est de poursuivre l'etude des portraits de phase pour des systemes dynamiques autonomes . Les courbes délimitant les divers domaines représentent les conditions de transition de phase. La dynamique des classes. Cette méthode a mis en place un système de valeurs avec des niveaux, en reprenant les besoins de la pyramide de .ans ce premier chapitre nous donnons tout d’abord la définition de la classe des systèmes dynamiques qui est étudiée dans le livre, ainsi que la terminologie et les notations utilisées, et nous l’illustrons avec divers exemples relevant des sciences de l’ingénieur. Une force correspond à l'action de pousser ou tirer et provient de l'interaction entre deux objets ou plus. En second lieu on définie le système de 1er ordre généralisé tout en montrant sa réponse . Nous pouvons légitimement définir de façon générale un système dynamique à l’aide de ce cas particulier. -Dans les oscillateurs auto-entretenus, ce sont les non-lin arit s qui fixent .
