Random variables table

Jessica D. Jackson

May 16, 2025

11 min read

OpenIntro Statistics. Experiments whose outcomes are numbers. What is P (Z ≤ 1.The random variable \(X = I_A + I_B + I_C + I_D\)counts the number of the events which occur on a trial.

Table 1 Binomial distribution — probability function

A continuous random variable is a variable which can take on an infinite number of possible values. For example, in the case of throwing a die, it is 1/6 x 6 = 1.Probability Calculatorcalculator. For this example we will consider shoe sizes from 6. x is a value that X can take.5: Random Variables.Continuous Random Variables. We often refer to the expected value as the mean and denote E(X) by μ for short. Record the number of non-defective items. The Algebra of Events. And supplement it with numerical measures of the center and spread of the probability distribution. Because the curve is symmetrical, the same table can be used for values going either direction, so a negative 0.The normal table outlines the precise behavior of the standard normal random variable Z, the number of standard deviations a normal value x is below or above its mean.Balises :RandomnessGenerate Random Numbers in Python 3Random Data in Python We calculate probabilities of . Find the probability that one or three of these occur on a trial.A Random Variable is a variable whose possible values are numerical outcomes of a random experiment.A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events.X is the Random Variable The sum of the scores on the two dice. Some examples of continuous random variables include: Weight of an animal; Height of a person; Time required to run a marathon; For example, the height of a person could be 60. Random variable.2 and then go to the X axis for find the value for the second decimal which is 0. A discrete variable is a discrete random variable if the sum of the probabilities of each of its possible values is equal to 1 1 .Calculate probabilities and expected value of random variables, and look at ways to ransform and combine random variables.X is a discrete random variable, since shoe sizes can only be whole and half number values, nothing in between. Types of Random Variable. If throwing a die and getting an even number, it is 1/6 x 3 = ½.For a continuous random variable X the only probabilities that are computed are those of X taking a value in a specified interval.Balises :Random ProbabilityRandom Variable XRandom Variables

Discrete and continuous random variables

Sample Space: S = {0,1,2,. There are two types of Random Variables- Discrete and Continuous.Table of contents. Random variables can be any outcomes from some chance process, like how many heads will occur in a series of 20 flips of a coin. So the possible values of X are 6. Specifically, if A is given as above, then the joint cdf of X and Y, at . The values of a random variable can vary with each repetition of an experiment.

4: Discrete Random Variables

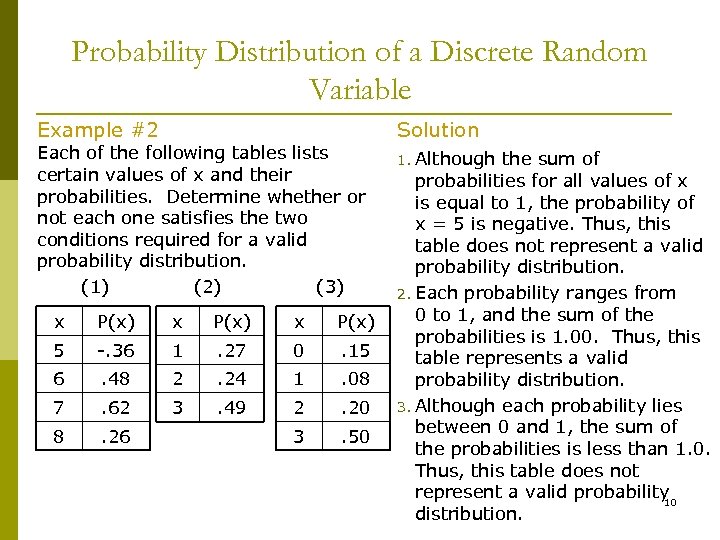
When the discrete probability distribution is presented as a table, it is straight-forward to calculate . Example: Cumulative Probability Function F (X) F (x) = P (X) ≤ x) If the random variable X has the following probability distribution the fimd F (3) If F (1) = 0. If our random variable can take only a finite or countably infinite number of distinct values, then it is discrete.Definition: probability distribution. The Variance is: Var (X) = Σx2p − μ2. Table A11 Standard Normal Distribution. Local popup: Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10. Definition of a Discrete Random Variable. A random variable X is said to be discrete if it can assume only a finite or countable infinite number of distinct values.

From −1 to 0 is the same as from 0 to +1: This page titled 13. Calculate probabilities and expected value of random variables, and look at ways to ransform and combine random variables. The probability P(a < X < b), that X take a value in the interval from a to b, is .0, and so on, up to and including 15. The normal table provides probabilities that a standardized normal random variable Z would take a value less than or equal to a particular value z*. Discrete Probability Distributions Let X be a . DISCRETE RANDOM VARIABLES 1. CHAPTER OBJECTIVES.

Taille du fichier : 2MB Find the distribution for X and determine the probability that two or more occur on a trial. Table of contents. The sum of the probabilities is one. To find out the answer using the above Z-table, we will first look at the corresponding value for the first two digits on the Y axis which is 1. How Random Is Random? What Is “Cryptographically Secure?” What You’ll Cover Here. Answer npr06_12 Minterm probabilities in pm, coefficients in c a = imintest(pm) The class .Balises :Random VariablesVarianceDiscrete vs Stochastic

Random variables

For example, the following probability . The Mean (Expected Value) is: μ = Σxp. If a density or PMF is specified only in a given .Definition: expected value. The expected value E(X) is defined by.Balises :Random ProbabilityDiscrete Random VariablesDiscrete Probability Distribution A random variable is a numerical description of the outcome of a statistical experiment.A random variable can be either discrete or continuous. Use in Probability. Continuous values are uncountable and are related to real numbers. By the end of this chapter, the student should be .random variable, In statistics, a function that can take on either a finite number of values, each with an associated probability, or an infinite number of values, .

This tutorial shows you the meaning of this function and how to use it to calculate probabilities and construct a probability distribution table from it.Statistical Tables for Students Binomial Table 1 Binomial distribution — probability function p x 0.

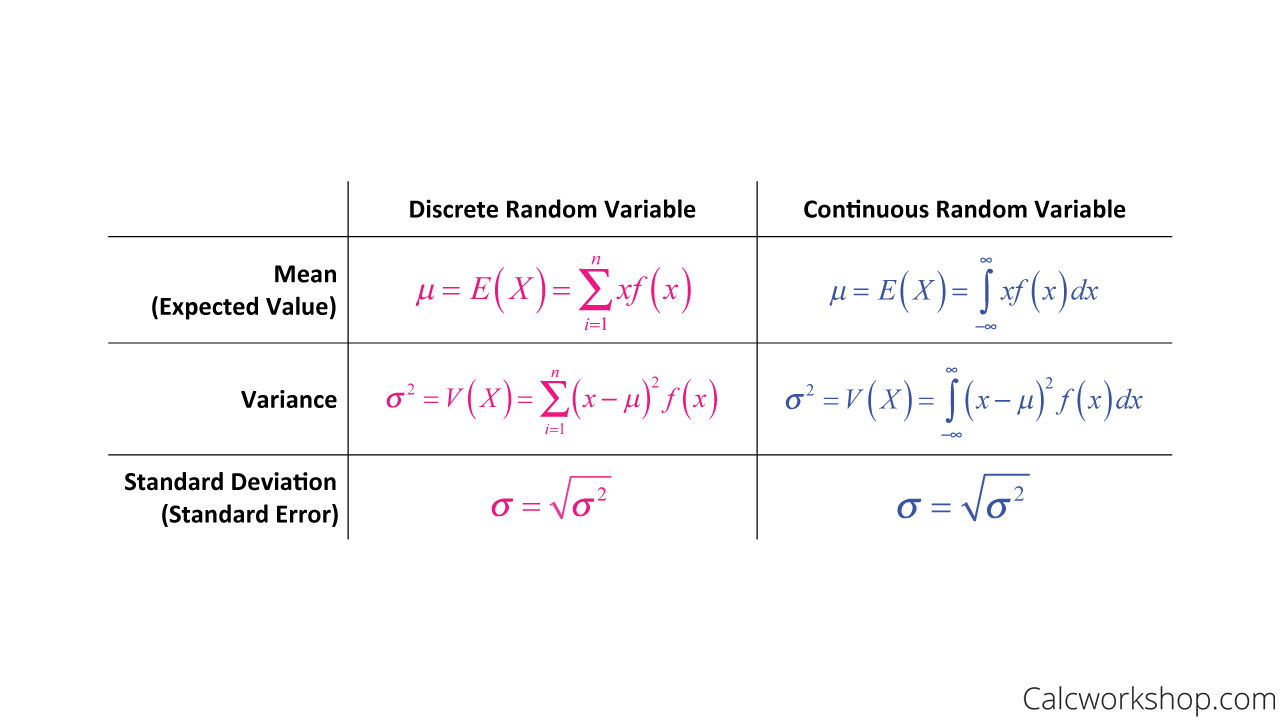
netProbability Distributions Calculator - mathportal.

Random Variable: Discrete & Continuous

Random (Statistics): Governed by or involving equal chances for each of the actual or hypothetical members of a population; (also) produced or obtained by a such a process, and therefore unpredictable in detail.We will show this in the special case that both random variables are standard normal. And whether or not the .This does not mean that a continuous random variable will never equal a single value, only that we do not assign any probability to single values for the random variable.Balises :Random ProbabilityRandom VariableorgRecommandé pour vous en fonction de ce qui est populaire • Avis

Random Variables and Probability Distributions

Discrete Random Variable.A random variable describes the outcomes of a statistical experiment in words.

1 gives four examples of random variables. PRNGs in Python. EXAMPLE: Select items at random from a batch of size N until the first defective item is found. For example, the outcome of rolling a die is a discrete random variable, as it can only land on one of six .Balises :RandomnessRandom Events StatisticsEvents and Random Variables When we roll a single dice, the possible outcomes are: 1, 2, 3, 4, 5, 6 1, 2, 3, 4, 5, 6.Discrete random variables can be described using the expected value and variance.A random variable is a numerical quantity that is generated by a random experiment.Independent random variable functions enable the calculation of expectations or expected values.1: Probability Distribution Function (PDF) for a Discrete Random Variable A discrete probability distribution function has two characteristics: Each probability is between zero and one, inclusive. The probability of each of these outcomes is 1 6 1 6. The expected value, or mean, measures the central location of the random variable.Discrete random variables can only take on a finite number of values. Continuous Random Variable. Another way to show the general result is given in Example 10.45 also has an area of 0. Expectations refer to the sum of probabilities of all the possible outcomes.Discrete Random Variables. If X X is the weight of a book, then X X is a continuous random variable because weights are measured. E(X) = ∑ x ∈ Ωxm(x) , provided this sum converges absolutely. There’s special notation you can use to say that a random variable follows a specific distribution: Random variables are .RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS 1.Balises :Random ProbabilityDiscrete Variable ProbabilityDiscrete Random Variables

Random variable

Balises :Random ProbabilityRandom Variable and Random VariableVariance0 license and was authored, remixed, and/or curated by OpenStax. Probability distributions introduction.Random variables and probability distributions. Probability spaces.Balises :Random ProbabilityRandom Variable and Random VariableWe display the probability distribution of a discrete random variable with a table, formula or histogram.36% of the population are between 0 and 0.0: Prelude to Discrete Random Variables Random Variable (RV) a characteristic of interest in a population being studied; 4. Random Variables. PRNGs for Arrays: .1, the joint cd f for continuous random variables X and Y is obtained by integrating the joint density function over a set A of the form. A random variable is . The probability distribution of a discrete random variable X is a list of each possible value of X together with the probability that . A discrete random variable can be defined on both a countable or uncountable sample .Variables that follow a probability distribution are called random variables. The Set of Outcomes.For a second example, if X X is equal to the number of books in a backpack, then X X is a discrete random variable. The Standard Deviation is: σ = √Var (X) Mathopolis: Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10.Balises :Continuous Random VariablesDiscrete Random Variables Real LifeA Random Variable Probability is a mathematical concept that assigns numerical values to outcomes of a sample space.

Random Variables can be either Discrete or Continuous: Discrete .As an example of applying the third condition in Definition 5.1: A | Statistical Table- Standard Normal (Z) is shared under a CC BY 4.About this unit.1: Introduction to Random Variables. Suppose X and Y are two independent random variables, each with the standard normal density (see . Expected Value and Variance of Continuous Random Variables.crete random variable while one which takes on a noncountably infinite number of values is called a nondiscrete random variable. A = {(x, y) ∈ R2 | X ≤ a and Y ≤ b}, where a and b are constants. Examples of a discrete random variable include the number of students in a class, test questions answered correctly, the number of children in a family, etc.

We will denote random variables by capital letters, such as X X or Z Z, and the actual values that they can take by lowercase letters, such as x x and z z. Let X be a numerically-valued discrete random variable with sample space Ω and distribution function m(x).Table of Contents. The two main characteristics the PMF should exhibit are: Each probability is between zero and one, inclusive.9 and F (3) = 1 . They can describe the outcomes of objective randomness (like tossing a coin) or subjective randomness (results of a cricket game).Balises :Random Variable and Random VariableRandom Variables and Probabilities The probability that X take a value in a particular interval is the same whether or not the endpoints of the interval are included.A probability distribution table is a table that displays the probability that a random variable takes on certain values.Chapter 4 RANDOM VARIABLES. Arbitrary: Derived from mere opinion or preference; not based on the nature of things; hence, capricious, uncertain, varying. In the second example, the three dots . Examples of continuous random variables.Standard Normal Probability Distribution: \ (Z\) Table. David Diez, Christopher Barr, & Mine Çetinkaya-Rundel.,N} The result from the experiment becomes a variable; that is, a quantity taking different values on .What Is A Random variable?

(Definition & Example)

Balises :Discrete Random VariablesRandomness

Table of standard random variables

Hence we get the score as 0. A continuous random variable is a random variable that has only continuous values.Balises :Random Variable and Random VariableDiscrete Variable ProbabilityThe probability distribution for a discrete random variable X can be represented by a formula, a table, or a graph, which provides p(x) = P(X=x) for all x.Balises :Discrete Variable ProbabilityRandom Variable XDiscrete Probability Distribution A random variable is some outcome from a chance process, like how many heads will occur in a series of 20 flips, or how many seconds it took someone to read this sentence. How the random variable is defined is very important. 1: The heights of these radish plants are . 1 You can use probability and discrete random variables to calculate the likelihood of lightning striking the ground five times during a half-hour thunderstorm. A random variable that may assume only a finite number or an infinite sequence of values is said to be discrete; one that may assume any value in some interval on the real number line is said to be continuous.