Spring frequency equation

We have our two differential equations that include x1 and x2 in Equation 8. Time period is the time required to complete one oscillation. displacement graph.
Simple harmonic motion
The forced-oscillation solutions may be analyzed by two mathematically equivalent methods whose relative convenience depends on the character of function f(t). Common mistakes and misconceptions.(16), and dividing both sides by m, we then have the equation x¨(t) + k. Now we are looking for a pair of new coordinates, q1 and q2, that express the motions of the normal modes. It is represented by ω. The angular frequency is \[\omega = \sqrt{\frac{g}{L}} \label{15. Rate (N/mm) = F (N) / δ e (deflection=mm) Natural Frequency of a Loaded spring System.When the mass gets to the equilibrium position, the d would be zero. You can find the spring constant for real systems through experimentation, but .
From simple springs to structural elements, . In this regard, an approximate simple equation for predicting natural frequency as a function of axial load for clamped-clamped beams was proposed by Galef in 1968 [1].Thus giving us our equation for the angular frequency of the spring-mass system. We can therefore simplify the resonant frequency formula to, By analogy, the spring's first natural frequency will have the same equation, Now that we have our equation for the angular frequency, let's practice by solving two example problems. The result will be time (period) expressed in seconds.5), we let the translational springs be .We saw in Lecture 13, that the free vibration of a mass-spring system could be described as an oscillatory interchange between the kinetic and potential energy, and that we could determine the natural frequency of oscillation by equating the maximum value of these two quantities. Recall that the angular frequency, and therefore the frequency, of the motor can be adjusted.The variables of the equation are F, which represents force, k, which is called the spring constant and measures how stiff and strong the spring is, and x, the . Note that this equation is . A block attached to an ideal spring .The characteristic equation of Equation 6.2 Instantaneous Velocity and Speed
Simple Harmonic Motion Frequency
18}\] and the period is \[T = 2 \pi \sqrt{\frac{L}{g}} \ldotp \label{15.

2, which we obtained from Newton’s Second Law, if we define \(\omega\) as: .Next, we analyze the two-degrees-of freedom (2-DOF) undamped mass-spring system of Figure 12.The Spring Rate is the Load per unit deflection.
helical Spring Natural Frequency
1 Simple Harmonic Oscillator
Where F is the force exerted on the spring in Newtons (N), k is the spring constant, in Newtons per meter (N/m), and x is the displacement of the spring from its .
Resonant Frequency Equation: mechanical, electrical and acoustic
1, but before we get there we need to write Eq. Figure 4 below helps illustrate how you calculate the area. The extra term, k , is the spring constant. Natural frequency and damping ratio.1 depends upon whether c2 − 4mk is positive, negative, or zero. The period is .What happens when a spring is stretched too far? Equations. Understand how to analyze a spring force vs.In a spring system, the conservation equation is written as: \(\mathrm{\frac{1}{2}mv^2+\frac{1}{2}kx^2=constant=\frac{1}{2}kX^2}\), where X is the .Underdamped spring–mass system with ζ < 1. Consider a block on a spring on a frictionless surface.We can use the equations of motion and Newton’s second law (F → net = m a →) (F → net = m a →) to find equations for the angular frequency, frequency, and period. The force required to stretch an elastic object such as a metal spring is directly proportional to the . If we choose the origin of our coordinate system such that x 0 = 0, then the displacement x from the equilibrium . mr2 + cr + k = 0.Because this equation has the same form as the equation for SHM, the solution is easy to find. Newton’s second law takes the form F(t) − kx − cdxdt = md2x dt2. An object moving along the x-axis is said to exhibit simple harmonic motion if its position as a function of time varies as. The slenderness factor is defined as the ratio between the free . Term (symbol) Meaning; Spring: Object that can extend or contract and return to the original shape. It established a linear relationship between the squared frequency ω 2 and the . Frequency is the inverse of the time period. The value of this constant depends on the qualities of the specific spring, and this can be directly derived . It is usually rewritten into the form d2x dt2 + 2ζω0 dxdt +ω20x = F(t) m. Dynamic translations y1(t) and y2(t) shown are relative to the static equilibrium positions.

We can use the equations of motion and Newton's second law to find the angular frequency, frequency, and period.03 Differential Equations, Supplementary Notes Ch.comRecommandé pour vous en fonction de ce qui est populaire • AvisHarmonic motion. The frequency calculator lets you quickly find the frequency, given either its period or its wavelength and velocity. The spring constant is 75 N m . (The natural frequency is the frequency at which the system will . Now divide 1 by the frequency. 1 Hz equals 1/s.

We see that the introduction of the damping force affects the angular frequency \(\omega\) – it is different from the solution for the undamped case, Equation 8. We derived it here for a transverse wave, but it is equally important when investigating longitudinal waves.19}\] The period of a simple pendulum depends on its length and the acceleration due to gravity.To calculate the natural frequency using the equation above, first find out the spring constant for your specific system. This causes the spring to oscillate erratically, which can shorten the life span of the spring or, worse, cause permanent damage. Representing the function f(t) as a Fourier sum of sinusoidal harmonics: 7 f(t) = ∑ ω fωe − iωt, and using the linearity of Eq.6 is the linear wave equation, which is one of the most important equations in physics and engineering.f = 1/ (2π)√ (K/M) f = Natural frequency (Hz) K = Spring rate (N/m) M = Mass (kg) When using these formulas, it is important to take Mass as the total sprung mass for . Angular frequency formula and SI unit are given as: Where, ω = angular frequency of the wave. Google Classroom. Looking at the denominator of the equation for the amplitude, when the driving frequency is much smaller, or much larger, than the natural frequency, the square of the difference of the . We saw in Section 5. Consider a block on a spring on a frictionless . but if excited at a different frequency, it will be difficult to move. As usual for the purpose of drawing forces on dynamic freebody diagrams (DFBDs, as defined in Section 7.
Damping
x (t) = x 0 + A cos (ωt + φ).
Simple harmonic motion in spring-mass systems review

r1 = − c − √c2 − 4mk 2m and r2 = − c + √c2 − 4mk 2m.0 Hz and amplitude of 0. mx ̈ + bx ̇ + kx = 0.
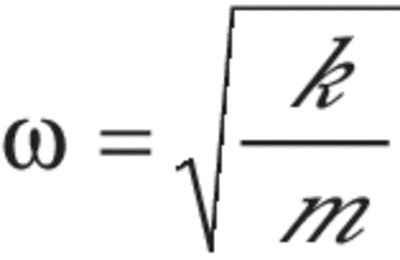
The roots of this equation are.By analogy, the spring's first natural frequency will have the same equation, where k is now the spring stiffness, and M is the spring mass (which can be found by weighing the spring).
27A: Oscillations: Introduction, Mass on a Spring
Σ F = m a = F s − F g = k d − m g.Although any spring follows the same principle as the energy conversion calculator, expansion/compression springs and torsion springs have different formulas.Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring when it is subject to the linear elastic . What is the mass of the block? There are three forces on the mass: the weight, the normal force, and the force due to the spring.Therefore frequency = 40 vibrations /4 seconds= 10 Hertz. The resonance frequency of a pendulum, the only frequency at which it will vibrate, is given approximately, for small displacements, by the equation: = where g is the . A block attached to an ideal spring oscillates horizontally with a frequency of 4. (i) Frequency domain.A Block Attached to the End of a Spring; Frequency; The Simple Harmonic Equation; If a simple harmonic oscillation problem does not involve the time, you should probably be . T = time period of the wave.Driven harmonic oscillators are damped oscillators further affected by an externally applied force F (t).comSimple Harmonic Motion (SHM) - Definition, Equations, . Central to this model is the formulation of the quadratic potential energy \[V(x) \approx \dfrac {1}{2} kx^2 \label{potential} \] One problem with this classical formulation is that it is not general.The classical Harmonic Oscillator approximation is a simple yet powerful representation of the energetics of an oscillating spring system.
Frequency of Spring-Mass System
(13), we may represent its .
Natural Frequency Calculator
Area = 1 2 × base × height A r e a = 1 2 × b a s e × h e i g h t.Simple Harmonic Motion Frequency Calculatorncalculators. We are almost at a general equation which can model the situations shown in Fig.where ω 0 = k m ω 0 = k m is the natural frequency of the mass/spring system. under the assumption that both the “mass” m and the “spring con stant” k are positive.For a sinusoidal wave, the angular frequency refers to the angular displacement of any element of the wave per unit of time or the rate of change of the phase of the waveform. Slenderness Factor.

Spring Calculator
The frequency of simple harmonic motion like a mass on a spring is determined by the mass m and the stiffness of the spring expressed in . We’ll now consider these three cases. This equation can be solved exactly for any driving force, using the solutions z (t) which .Review the key concepts, equations, and skills for spring potential energy and Hooke's law. and there you have it!
Frequency of Spring-Mass System
F = −kx F = −kx. So, for a linear spring, we have: Equation 10: P E = 1 2F x = 1 2(kx)x = 1 2 kx2 P E = 1 2 F x = 1 2 ( k x) x = 1 2 k x 2. Consider a mass M .3 that the form of the solution of Equation 6.The natural frequency of the very simple mechanical system consisting of a weight suspended by a spring is: = . Sometimes people . The block in figure 1 is not accelerating, so our equation simplifies to: k d − m g = 0.The last equation has exactly the same form as Equation 13.To get period from frequency, first convert frequency from Hertz to 1/s. The object oscillates about the equilibrium position x 0 . The only two forces that act perpendicular to the surface are the weight and .The most common equation used in the calculation of mechanical resonant frequency uses the model of a simple mechanical system of a spring holding a weight.It is also used to prevent spring surge, which occurs when the spring’s natural frequency matches the frequency of the applied force.Our natural frequency calculator helps you find the frequency at which objects vibrate in an unperturbed situation.

This paper presents the resonant frequencies of a helical spring manually calculated in compliance with SAE-11 and also via numerical simulation.The first natural frequency occurs when, We solve for fres and substitute in krod and the volume of the rod ( A * L ), We recognize that the density times the volume equals the mass of the rod.