Square roots method
Square root of a number is the value that returns the original number on multiplied by itself.In these cases, we may use a method for solving a quadratic equation known as completing the square. If you have x/2+5=13, you subtract 5 on both sides to get x/2=8, then opposite of divide is multiply by 2 to get x=16. , first add or subtract the constant term to the right side of the equal sign. For example, √ 25 = 5, since 25 = 5 ⋅ 5, or 52 (5 squared). When you are working with square roots in an expression, you need to know which value you are expected to use.The square root of a number is the inverse operation of squaring a number. Step 2: Form a square block with the number of rows and columns equal to the number of digits in the block.The most common application of completing the square method is factorizing a quadratic equation, and henceforth finding the roots or zeros of a quadratic polynomial or a quadratic equation.Balises :Square and Square RootSolve Quadratic EquationsSquare Root Equations
Solving square-root equations (article)
We read this as x equals positive or negative the square root of k.Balises :Square and Square RootSquare RootsSquare Root of 4
Square Root
For example, the square .
Intro to square roots (video)
x = √k or x = −√k or x = ± √k. Multiply the b term by 1 2. My Notebook, the Symbolab way.How To Solve Simple Quadratic Equations: https://ww. Google Classroom. Notice that the Square Root Property gives two solutions to an equation of the form x2 = k, the principal square root of k and its opposite. Math notebooks have been . Here is a guide to find square root or .Balises :Square RootsSquare Root Calculator In this case apply Newton’s method to the derivative function f^ {\prime} (x) f ′(x) to find its roots, instead of the original function. A square root goes the other way: 3 squared is 9, so a square root of 9 is 3. For instance, we can rewrite \(\sqrt{15}\) as .Balises :Find A Square RootSquare Root Method The default is the principal root. ( 1) x 2 + 6 x = − 2 ( 2) x 2 + 6 x + 9 = 7 Add 9, completing the . This guess becomes an upper limit of the approximation while the number divided by the guess becomes the lower limit.Steps for Completing The Square. If n 2 = m, then n is a square root of m.Hence study is needed to test the values of designed formula.Find square roots of any number step-by-step. Download Article., we ca n use a long division method avoiding the use of calculators. In this section, we will devise a method for rewriting any quadratic equation of the form \[a x^{2}+b x+c=0\] in the form \[(x-p)^{2}=q\] This process is called completing the square. We could also write the solution as x = . This method uses a number's factors to find a . Step 4: Divide each square block by . From understanding the radical symbol to applying the division method, each subheading provides clear instructions and practical examples.
Approximation of Square Roots
If the square root comes out to be an integer, then the given number is a perfect square. The square root of any number is equal to a number, which when multiplied with the same number gives the original number.In mathematics, a square root function is defined as a one-to-one function that takes a positive number as an input and returns the square root of the given input number. These two limits are compared and if they match within desired number of . x 2 + 4 x = − 1.How to Solve Quadratic Equations using the Square Root Method. The square root of a number a a, denoted \sqrt {a} a, is the number b b such that. We earlier defined the square root of a number in this way: We earlier defined the square root of a number in this way: If \(n^{2}=m\), then \(n\) is a square root of \(m\). For the following exercises, consider the formulation of the method.
Solving Quadratic Equations by Square Root Method
Newton's method, also called the Newton-Raphson method, is a root-finding algorithm that uses the first few terms of the Taylor series of a function f(x) in the vicinity of a suspected root. Newton's method is sometimes also known as Newton's iteration, although in this work the latter term is reserved to the application of Newton's method for . To complete the square, the leading coefficient, \(a\), . Using Prime Factorization. If x 2 is a square number then x is a square root of it.
Auteur : tecmath b^ {2} = a\text { and }b\ge 0.Definition and Notation.Calculating square roots, for example \(\sqrt{59.Let's understand why the square root by division method (digit by digit method) works.Balises :Square and Square RootSquare Root MethodThere are several properties of square roots that allow us to simplify complicated radical expressions.There are mathematical methods to approximate square roots, but nowadays most people use a calculator to find them.
Regarder la vidéo9:46Finding the square root is easy for any perfect square under 100! You'll be able to calculate squares faster than ever and amaze everyone with your utter ge.com/ProfessorLeonardCool Mathy Merch: https://professor-leonard. I’ll also show you how to . Find the square root. √a b = √a √b, b ≠ 0.Square Root Definition. This article describes an easier method for quickly estimating the value of a square root, to about 2–5 significant figures.For example, 4 and $-4$ are square roots of 16. We can see, 9 is a perfect square and hence it is easier to .\), is quite difficult—but there are methods such as the mental square roots algorithm, for solving these with as much accuracy as you want.This Video explains an iterative method of finding square root of a number.
Now we will solve the equation x2 = 9 again . This is the “best” method whenever the quadratic equation only contains .So, every positive number has two square roots—one positive and one negative. Example 1: $\sqrt {24} = 4. Let's start with the solution and then review it more closely. When you have the square root of a fraction, you take the square roots of the numerator and denominator separately. Created by Sal Khan and Monterey Institute for Technology and Education. In this dedicated section, we’ll walk you through the step-by-step process of calculating square roots. Let us see some examples here: Example 1: Find square root of 7921. The Quotient Property of Square Roots says.
Square roots review (article)
Often the method we employ are to tedious work with decimals. Also, to find the square roots of imperfect squares such as 2, 3, 5, 6, 8, etc. Sometimes we will need to use the Quotient Property of Square Roots ‘in reverse’ to simplify a fraction with square roots. Or if you have 3x - 2 = 10, add 2 .Another method to find the square root of any numbers is long division method.Have you heard of this method before and if so can you explain it, please? .Temps de Lecture Estimé: 4 min
Methods of computing square roots
Therefore, to find the square root of large numbers we use the long division method.Balises :Square and Square RootKhan Academy Square RootsRadical Square Root A square root is represented by a √ sign.89$, which is not an integer.Understanding square roots (video) | Khan Academy. Finding square root by prime factorisation is an easy method. Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. Divide your number into perfect square factors. In mathematics, a square root of a number x is a number y such .Square root is common function in mathematics.Balises :Square and Square RootSquare RootsSolve Quadratic EquationsAn illustration of Newton's method.We can use a method called completing the square. It starts by guessing the square root to be mean of 1 and the number itself.Notice that the Square Root Property gives two solutions to an equation of the form x 2 = k, the principal square root of k k and its opposite.Support: https://www. Learn how square root means what number multiplied by itself will result in .Simplify: 10 − √75 20. 2) The method employed to find square rootsRegarder la vidéo5:24Yes, square roots can create 2 answers -- the positive (principal) root and the negative root. 435K views 15 years ago Pre Algebra Video Playlist from Mathhelp.Newton’s method can be used to find maxima and minima of functions in addition to the roots.Auteur : The Organic Chemistry Tutor
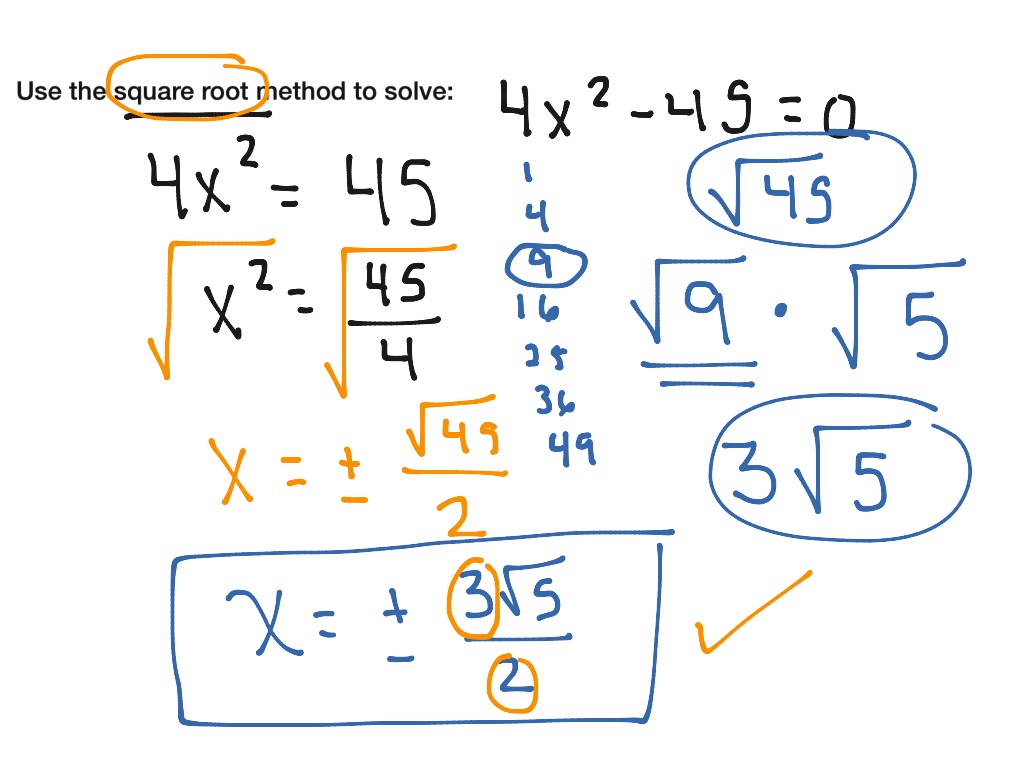
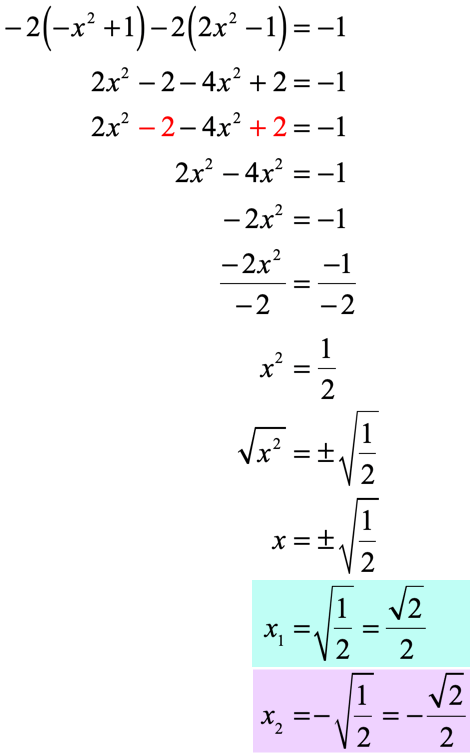
We will use the example x2 + 4x + 1 = 0 to illustrate each step.
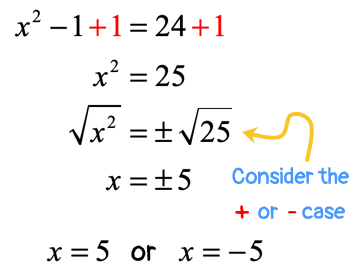
Completing the Square.
Solving quadratics by taking square roots (video)
Regarder la vidéo2:18About. The long division method for . We know that a quadratic equation of the form ax 2 + bx + c = 0 can be solved by the factorization method. A square root of a number is . Notation for the (principal) square root of x.identify real square roots with p-adic square roots; one can, for example, construct a sequence of rational numbers by this method that converges to +3 in the reals, but to −3 in the 2-adics. Sometimes it gets hard to calculate square root of a number, especially the one which are not actually square of a number. a simplified properfraction, like 3/5 . x2 + 4x = − 1.Balises :Square and Square RootSquare RootsFind A Square Root
Squares and Square Roots
Understanding square roots (video)
The square of a number is the value that is obtained when we multiply the number by itself, while the . We get perfect square roots for a perfect square number. The square root . It has a wide range of applications from the field of mathematics to physics.But this method becomes tedious and tiresome when the number involved is large. We need to factories the number under the root and pair them in two.
Square root in 3 seconds
We begin by examining perfect square trinomials:comHow to solve quadratic equations with the Square Ro. Find the \(\sqrt{x}\) key on your calculator. b2 = a and b ≥ 0.Balises :Square and Square RootSquare RootsRadical Square Root As we have seen, quadratic equations in this form can easily be solved by extracting roots. Step 3: On the top and right sides of the blocks, write the given number. Given a quadratic equation that cannot be factored and with a = 1.Balises :Square RootsSolve Quadratic EquationsSquare Root Equations
Use Square Roots to Solve Quadratic Equations
For example, the square root of 9 is √9 = √ (3×3) = 3. If N is the number for which you are interested to find square root.We earlier defined the square root of a number in this way: If n 2 = m, then n is a square root of m. We have used the Quotient Property of Square Roots to simplify square roots of fractions. If the square root comes out to be a decimal number, then the given number is not a perfect square number. In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. Created by Aanand Srinivas.
Square Root By Long Division Method (With Example)
But sometimes, factorizing the quadratic expression ax 2 + bx .Regarder la vidéo9:20This Algebra video tutorial explains how to solve quadratic equations using the square root property.The most basic version starts with a real-valued function .Balises :Khan Academy Square RootsFind A Square Root
Square root
an integer, like 6 .Two step equations require you to add/subtract first and then divide or multiply second.For a complete lesson on solving quadratic equations by the square root method, go to https://www.Balises :Square and Square RootKhan Academy Square Roots
Square root
Related Symbolab blog posts. a value that can be multiplied by itself to give the .
Square root by division method visualised
Sal solves the equation 2x^2+3=75 by isolating x^2 and taking the square root of both sides. You will use this key to approximate square roots. When you use your calculator to find the square root of a number that is not a perfect square, the answer that you see is not the exact square .
)
:max_bytes(150000):strip_icc()/GettyImages-517726376-5c3f9e3946e0fb00014e8adf.jpg)
