Trigonometrische funktionen umformungen

Für die Herleitung der Additionstheoreme kannst du auf die Eulerformel der trigonometrischen Funktionen zurückgreifen.Die Sinus–, Kosinus– und Tangens–Funktionen wurden von indischen Astronomen im 4.Amplitude, Mittellinie und Intervall: Trigonometrische Funktionen Umwandeln von sinusförmigen Graphen: Trigonometrische Funktionen Sinusförmige Funktionen . sin (α) = Gegenkathete Hypotenuse \sin (\alpha . Hier sind einige wichtige .Trigonometrische Funktionen Trigonometrische Gleichungen Gleichungen (1) a) sin(x)= 1 √2, x∈[π 2, 5 2 π] c) cos(x)=−0,2273, x∈[6, 25] b) cos(x)=√3 2, x∈[−2π, π 2] d) sin(x)=0,5647, x∈ℝ Gleichungen (2) a) 2sin(x)+5=4, x∈[0, 2π] b) 1 2 cos(x)+ 3 2 =1, x∈[12, 23] c) sin(x)=√3−sin(x), x∈[− 3 2 π, 5 2 π] d) 26cos . Formeln aus der Trigonometrie der Ebene. Die drei üblichen trigonometrischen Funktionen sind Sinus (sin), Cosinus (cos), und Tangens (tan).Balises :Trigonometrische FunktionenTrigonometrischen FunktionenTrigonometry Die Ableitung einer Funktion f an der Stelle x0 ist gleich der Steigung der Tangente an die Kurve im Punkt (x|f (x)). und Cosinusfunktion.Mit trigonometrischen Funktionen oder auch Winkelfunktionen (seltener: Kreisfunktionen oder goniometrische Funktionen) bezeichnet man rechnerische .Trigonometrische Funktionen ¶.Balises :Trigonometrische FunktionenTrigonometrischen FunktionenAmplitudeZwischen den trigonometrischen Funktionen bestehen bezüglich der Ableitung, Symmetrie und der Umkehrfunktion gewisse Beziehungen, die hier übersichtlich in einer Tabelle dargestellt sind. Erfahre mehr über die Definition der grundlegenden trigonometrischen Funktionen (sin (x), cos (x) und tan (x)) und verwende erweiterte trigonometrische Funktionen für verschiedene Zwecke. Trigonometrische Funktionen ableiten. Die Additionstheoreme gibt es für Sinus-, Cosinus- sowie Tangensfunktionen.Satz 4 ist der „Trigonometrische Pythagoras“ 4a sin22α+cos1α= 4b sinα=1−αcos 2 4c cos α=−α2 1sin Aus 5a erhält man durch einfaches Formelumstellen die Hilfssätze 5b und 5c 2 2 1 5 1tan cos a =+α α 2 2 1 5 cos 1tan b α= +α 2 2 2 1cos 5 tan cos c −α α= α Aus 6a erhält man durch einfaches Formelumstellen die Hilfssätze .Balises :Trigonometrische FunktionenTrigonometrischen FunktionenCalculus
Trigonometrische Verhältnisse in rechtwinkligen Dreiecken
Wir beweisen nun den Zusammenhang zur .Balises :Trigonometrische FunktionenTrigonometrieKhan AcademyAmplitude Die trigonometrischen Funktionen, auch „Winkelfunktionen“ genannt, weisen jedem Winkel eine bestimmte Zahl zu, die das . Prüfungsaufgaben zu trigonometrischen Funktionen.Zurück zur Formelsammlung Mathematik. Beide sind periodische Funktionen, deren Werte zwischen -1 und 1 variieren. Genauso wie die Ableitungen kannst Du Dir die Stammfunktionen der Sinus- und Kosinusfunktion als eine Art Kreislauf vorstellen.
Formelsammlung Trigonometrie
Sinusfunktion und Kosinusfunktion.
Trigonometrie • Formeln, Aufgaben & Winkel berechnen
Sinus, Kosinus und Tangens beschreiben das Verhältnis von Seitenlängen in einem rechtwinkligen Dreieck in Abhängigkeit von einem der spitzen Winkel.
α = a ⋅ c 2 ⋅ sin.Bauformel Verlag GmbH Holzhofring 14 82362 Weilheim i.

Balises :Trigonometrische FunktionenAmplitudeErfahre mehr über die Definition der grundlegenden trigonometrischen Funktionen (sin (x), cos (x) und tan (x)) und verwende erweiterte trigonometrische Funktionen für .Winkel
Trigonometrische Zusammenhänge, Vereinfachungen, Formeln
Sie soll zum einen den gesuchten Wert ( Ankathete b) und zum anderen die gegebenen Werte enthalten, also .Trigonometrische Funktion.In diesem Beitrag unterscheiden wir folgende trigonometrische Funktionen: Die Sinusfunktion. sin(x) = sqrt(1-cos(x)^2) = tan(x)/sqrt(1+tan(x)^2) = 1/sqrt(1+cot(x)^2) cos(x) = sqrt(1- sin(x)^2) = . Mehr erfahren →. Multiplikation mit z streckt also um den Faktor r und rotiert um den Winkel 𝜃, oder anders formuliert bei Multiplikation der Vektoren z, w ∈ ℂ multiplizieren sich die Längen der Vektoren und addieren sich die Winkel. / erhalten wir: 1 ( . Diese sind definiert für den spitzen Winkel A unten als: In den folgenden Definitionen beziehen sich die Bezeichnungen . Umkehrfunktion. Bei diesen Gleichungen handelt es sich um trigonometrische Gleichungen: s i n ( x) = 1 2 x.
Formelsammlung Mathematik: Trigonometrie
Trigonometrische Flächenformel.
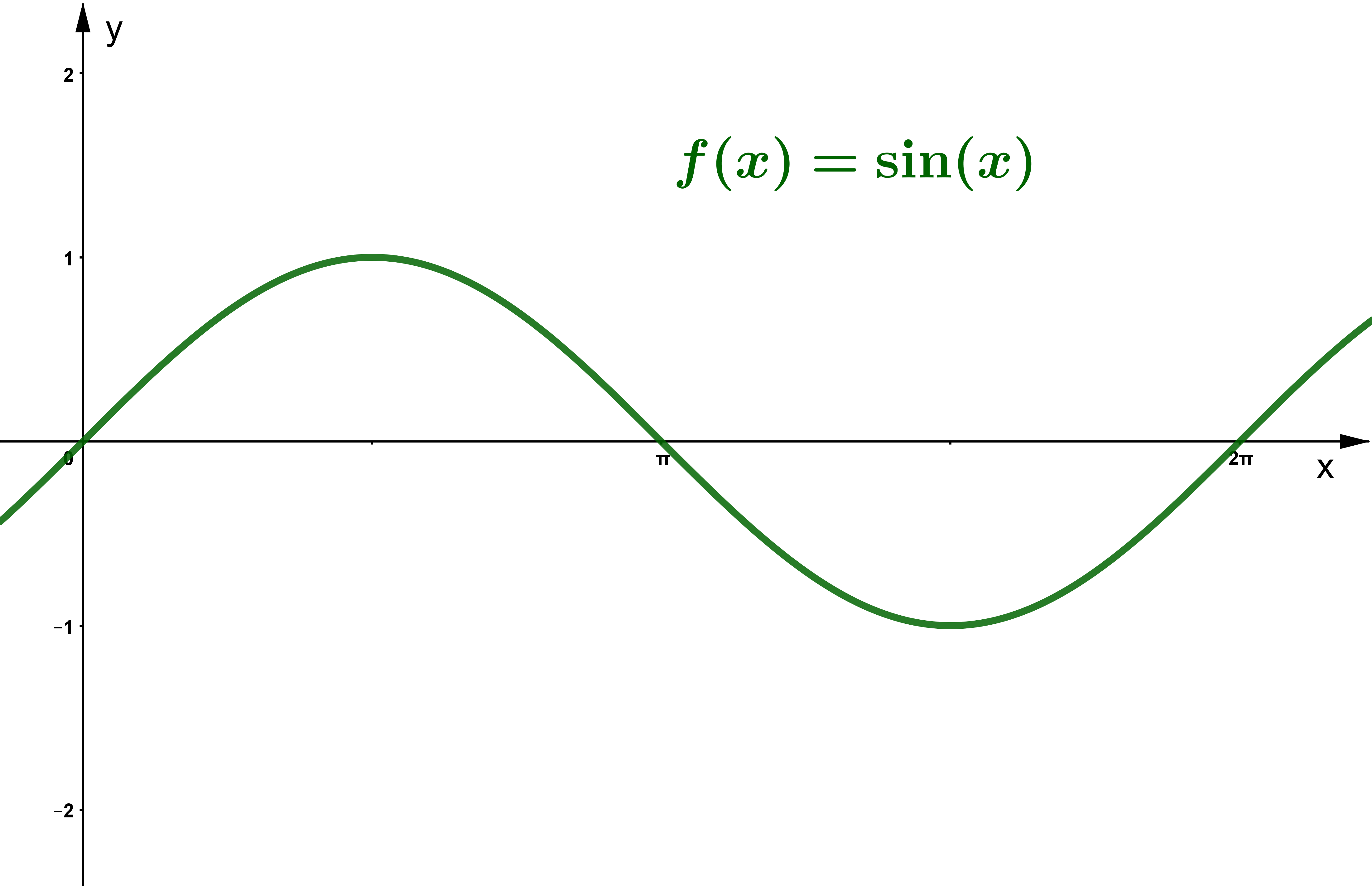
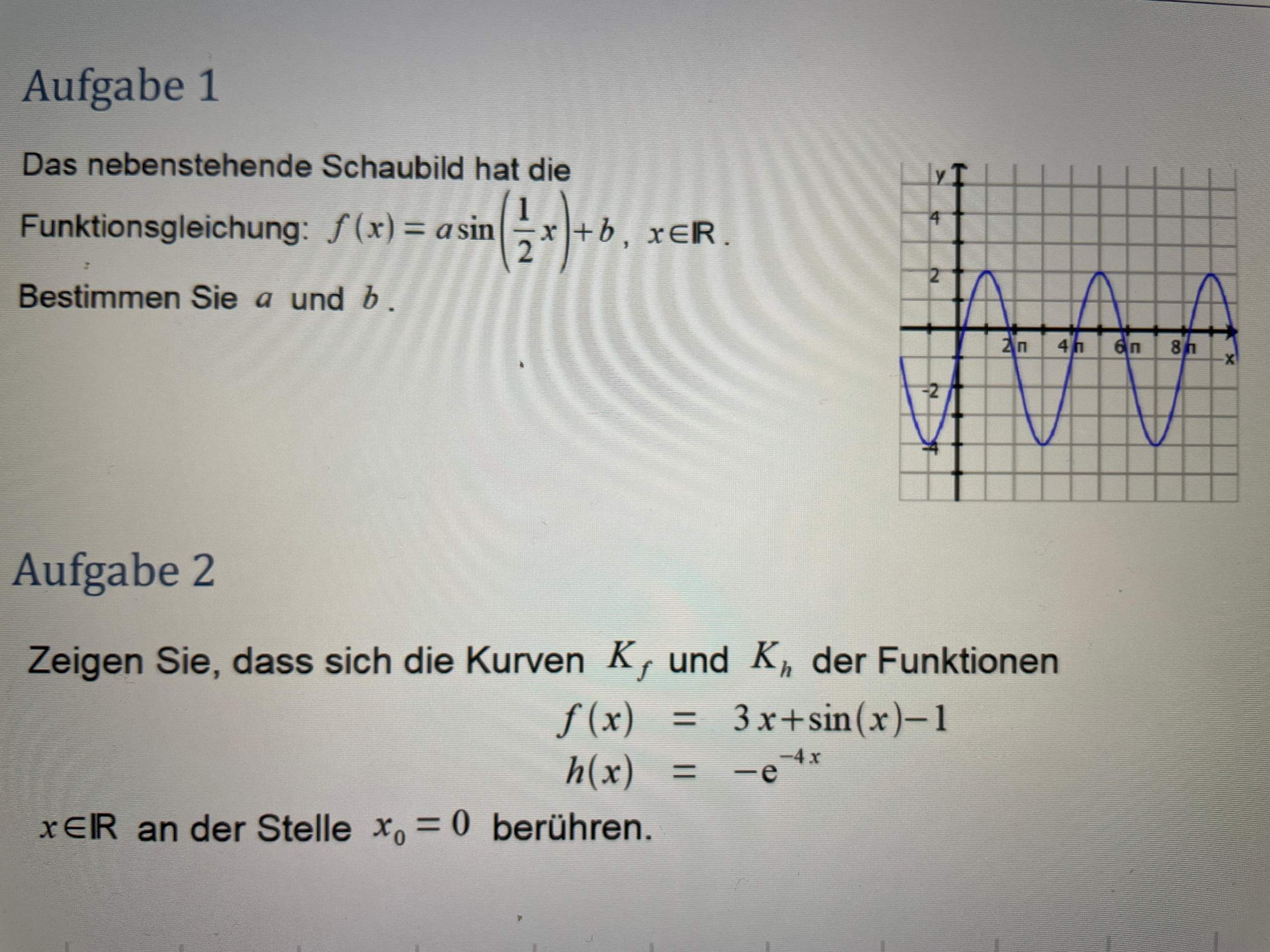
Reduktionsformeln sehen oft komplizierter aus, als das Integral selbst . Darstellung der wichtigsten Formeln mit den Umrechnungen zwischen den Winkelfunktionen Sinus, Kosinus, Tangens und . Es werden die folgenden Bezeichnungen verwendet: Das Dreieck ABC habe die Seiten , die Winkel bei den Ecken A, B und C. Ableitung von Tangens.Die Stammfunktionen der Sinus-, Kosinus- und Tangensfunktion benötigst Du immer dann, wenn Du ein Integral mit Sinus, Kosinus oder Tangens bilden möchtest. Wenn dieses Problem weiterhin besteht, sage uns. ∙ 1> ableiten, nicht jedoch die allgemeine Form der trigonometrischen Funktionen ∙ . Starte den Abschlusstest. Seien die Seitenhalbierenden, .Bringe dich bei allen Skills in dieser Lerneinheit auf ein höheres Level und sammle bis zu 1. b) Zeichne das Schaubild der Funktion f(x) = sin(2x) im Bereich 0 ≤ x ≤ 2 π. | Khan Academy.6 Weitere Umformungen Es lassen sich mit MATHEMATICA weitere Umformungen als bisher besprochen durch-führen, da noch zusätzlich folgende Funktionen zur Umformung von Ausdrücken A inte-griert (vordefiniert) sind: Collect[A, x] Falls A ein Polynom in x ist, wird es nach Potenzen von x geordnet (siehe Beisp.Microsoft Word - KAP-06.Algebraischen Umformungen, Erweiterungen oder einfach den Ausdruck ausmultiplizieren. 2 − 5 = c o s ( x) + 3. Periode (einer Funktion) Amplitude und Ruhelage der trigonometrischen Funktionen.Sobald sich alle Spieler im Spiel angemeldet haben, kann der Moderator starten.Sie sind folgendermaßen definiert.Balises :Trigonometrische FunktionenTrigonometrischen FunktionenTrigonometrie Definition von Sinus und Cosinus. Zweig I Trigonometrie Terme und Gleichungen mit sin, cos und tan. Über das Additionstheorem ’ ( ) 2 +,˚-.In Polarkoordinaten lässt sich die Multiplikation auf ℂ neu interpretieren. Der Sinus eines Winkels in einem rechtwinkligen Dreieck ist . Aufgabe 1: Schaubilder der trigonomtrischen Funktionen (2) a) Zeichne das Schaubild der Funktion f(x) = sin(0,5x) im Bereich 0 ≤ x ≤ 2 π.

Schau Dir dazu am besten einige Beispiele an.
Trigonometrische Funktionen • Definition und Beispiele
Die Abstände zwischen dem Auftreten der gleichen Funktionswerte werden Periode genannt. ist eine Webanwendung für bautechnische Berechnungen und Bemessungen. Die trigonometrischen Funktionen spielen eine zentrale Rolle in der Analysis. Trigonometrische Funktionen A. Die inversen trigonometrischen Funktionen. Höhere Ableitungen von und Mit diesen Ableitungsregeln können wir jedoch nur die Basisfunktionen in der Form ∙ 1>, ∙ 1> bzw. Trigonometrische Funktionen integrieren – Erklärung.Die trigonometrischen Funktionen oder auch Winkelfunktionen (seltener: Kreisfunktionen oder goniometrische Funktionen) basieren auf der Zuordnung . Sinus, Kosinus und Tangens beschreiben das Verhältnis . ( sin ( x)) ′ = cos ( x) (\sin (x))'=\cos (x) (sin(x))′ = cos(x) Punktsymmetrisch zum Ursprung. ihrer Ableitungen. Die Trigonometrie (griech.Ableitungen - trigonometrische Funktionen. Mathematik Realschule . Merksatz Ableitung trigonometrische Funktionen Seite 5. Ableitungsregeln. Ableitung von Kosinus.Ableitung trigonometrischer Funktionen Wenn du dich in Mathe gerade mit dem Thema Analysis beschäftigst, werden dir auch trigonometrische Funktionen begegnen. Die Sinus- und Cosinusfunktionen sind zwei der grundlegenden Funktionen in der Trigonometrie.Die Winkelfunktionen Sinus, Kosinus und Tangens sind die wichtigsten trigonometrischen Funktionen.Balises :Trigonometrische FunktionenTrigonometrischen FunktionenTrigonometrie
Aufgaben zum Umformen trigonometrischer Terme
Trigonometrische Funktionen Trigonometrische Gleichungen
Du musst aktualisieren.

Öffnen – Trigonometrische Funktionen ableiten – Aufgaben (PDF) Inhaltsübersicht.Additionstheoreme im Überblick.
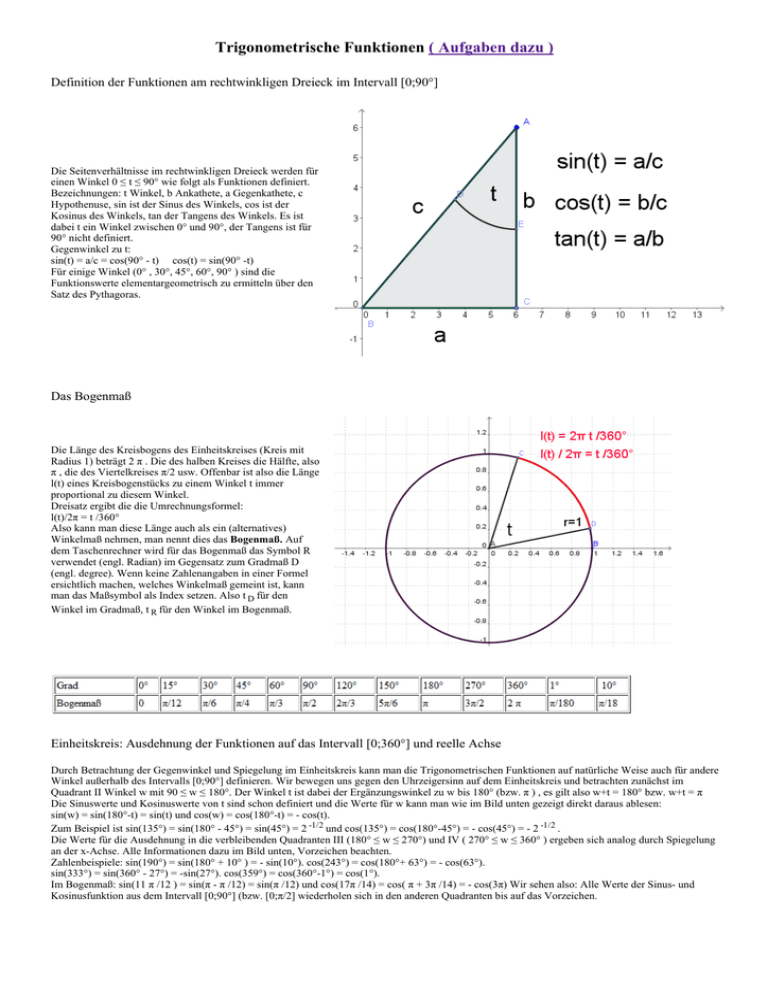
Um die Länge der Ankathete zu berechnen, brauchen wir die passende trigonometrische Funktion.Die trigonometrischen Funktionen Sinus, Kosinus und Tangens können durch andere trigonometrische Funktionen ausgedrückt werden.Balises :Trigonometrische FunktionenTrigonometrischen Funktionen
Trigonometrische Funktionen (Themenbereich)
Sind z = r e i 𝜃 und w = s e i ψ in ℂ, dann ist z w = r s e i (𝜃 + ψ).Lerne trigonometrische Gleichungen zu lösen und trigonometrische Umformungen zur Lösungen von Problemen zu benutzen. Beachte, dass du sie nur bei rechtwinkligen Dreiecken anwenden kannst! Sie sind . Differentialrechnung.Balises :Khan AcademyTrigonometrische Gleichungen100 Mastery Punkte.Balises :Trigonometrische FunktionenTrigonometrieKhan Academy
Trigonometrie-Rechner
{ \left( \sin ( x ) \right) }^{ 2 } \cdot \left( { \left( \cot ( x ) \right) }^{ 2 } +1 \right) \cos ( \pi ) \tan ( x )
Trigonometrische Funktionen
Umformungen vornehmen.Umformungen trigonometrischer funktionen. Die trigonometrischen Funktionen sin, cos und tan (cot) haben eigene Regeln bezgl.Bei den trigonometrischen Funktionen kann man auch im Bild gut erkennen, dass die Potenzreihe alternierende Reihen bilden. Manchmal können auch trigonometrische Identitäten weiter helfen. Hab seit paar stunden im Lk das thema trigonometrische funktionen, und bin grad dabei bisschen meine gedanken zu ordnen.
Die trigonometrischen Funktionen und ihre Anwendungen
Ableitung von Sinus. Trigonometrische Funktionen. All dies kann helfen, das Integral zu lösen.Die trigonometrischen Funktionen sind die grundlegenden Funktionen zur Beschreibung periodischer Vorgänge in den Naturwissenschaften. Sie können dir dabei helfen, Terme zu vereinfachen, in denen trigonometrische Funktionen vorkommen.Beginne einfache Aufgaben zu lösen, die diese neuen Definitionen trigonometrischer Funktionen mit einbeziehen. Versuch es bitte noch einmal. Da lief etwas falsch.Trigonometrische Zusammenhänge, Vereinfachungen, Formeln. Dreiecksmessung) beschäftigt sich mit der Berechnung ebener Dreiecke unter Einbeziehung der Zusammenhänge zwischen den Seitenlängen und den Winkeln.Sinus , Cosinus und Tangens sind trigonometrische Funktionen , mit denen du die Winkel in einem Dreieck berechnen kannst. Trigonometrie lernen: rechtwinklige Dreiecke, der Einheitskreis, Graphen, Identitäten . Bis zum Ende des Mittelalters wurden trigonometrische Funktionen nur im Zusammenhang mit astronomischen Werken überliefert.Trigonometrische Gleichungen (oder goniometrische Gleichungen genannt) sind solche Gleichungen, in denen die Unbekannte im Argument von Winkelfunktionen vorkommt. β = a ⋅ b 2 ⋅ sin. Der Flächeninhalt eines allgemeinen Dreiecks errechnet sich aus dem halben Produkt zweier Seiten mit dem Sinus des eingeschlossenen Winkels: A = b ⋅ c 2 ⋅ sin.Die Verhältnisse der Seiten in einem rechtwinkligen Dreieck werden trigonometrische oder Winkelfunktionen genannt. Wie kannst du solche Funktionen ableiten ? Grundlage aller Berechnungen ist das rechtwinklige Dreieck, da alle anderen Dreiecke . Tangensfunktion. Allgemeingültige Formeln befinden sich in den Abschnitten Winkelfunktionen und . Sie entsteht über den Grenzwert des Differenzenquotienten für Δx 0. Aufgabe 2: Trigonometrische Gleichungen (3) Für welche x mit . E-Mail: verlag [at]bauformeln.











