Twin primes formula
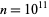
distribution of zeros, some zeros are calculated twice.orgHow do we identify twin primes - Mathematics Stack .
Introduction to twin primes and Brun's constant computation
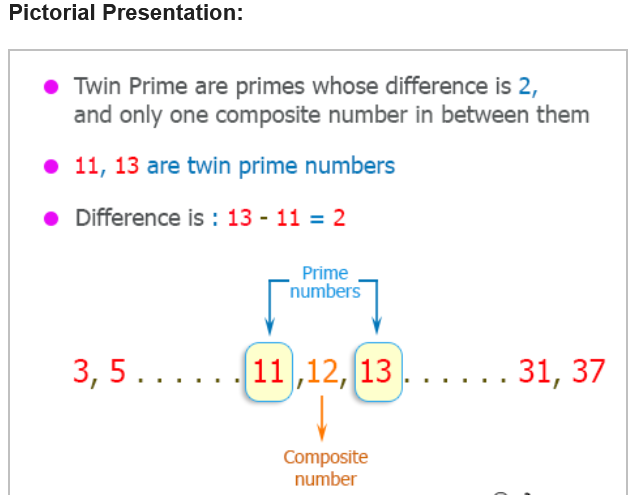
The calculated zeros provide evidence tow ards the twin prime hypothesis. (The proof's method is set-theoretic.Balises :Twin PrimesUlam spiral Prime numbers are numbers that can only be divided by themselves and 1.Twin prime numbers can be defined as a set of two numbers that have only one composite number between them.Twin primes are two prime numbers that have a difference of 2 between them. A twin Prime Pair is a pair of prime numbers (a,b) such that a is less than or greater than b by 2. Except for the couple (2; 3); this is clearly the smallest possible distance between two primes.
+ O(x1/2+ǫ), t. In this paper, we will consider its cousin “the twin prime counting function” that we will denote by . That in itself is probably worth a Fields medal. The first twin primes are {3,5}, {5,7}, {11,13} and {17,19}. While the proof of the twin prime conjecture is a distant goal, Heath-Brown proved in 1983 that if there are infinitely many Siegel zeros, then there are infinitely many twin primes. If we put it in a simple manner, twin prime .org/numberphile for Brilliant and get 20% off their premium service (episode sponsor)More links & stuff in full de. Divisibility Test Calculator.Balises :DefinitionTwin Primes ConstantIntroductionViggo Brun
Twin Prime Distribution
related primes, both in relation to number theory as a whole, and as specific, well-defined problems.In 2000, he wrote A Formula for the Fine Structure Constant, a formula that was associated with his Twin Prime Theorem. Another definition of twin prime numbers is – the pair of numbers with a difference of two are also called twin prime numbers. as known , each prime number greater than 3 . Viewed 4k times.If there was a closed formula for the nth twin prime, we'd know whether there is a finite or infinite number of them too. Modified 2 years, 9 months ago. One of the first results of looking at twin primes was .twin prime Twin primes are pairs of primes which differ by two.Last Updated : 01 Apr, 2024.; These numbers are . Asked 9 years ago. On May 13, an obscure mathematician — one whose talents had gone so unrecognized that he had worked at a Subway restaurant to .Definition 1 A couple of primes (p; q) are said to be twins if q = p+2.Balises :Prime numberNumber TheoryTwin Primes ConjectureConjecturesTwin primes are pairs of primes which differ by two. There are two related conjectures, each called the twin prime conjecture. I havent tried the Atkin Sieve. They can also be defined as the pair of .
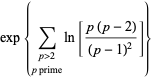
Based on Cramer model (without even numbers) the number of twin primes in [1,. For example (41,43) - A twin prime numbers with prime difference of two. Sometimes the term twin prime is used for a pair of twin primes; an . The uniform presents symmetry in terms of k that works as single index in sieving. “We’ve been stuck . @frodo I tried . Since can increase by at most 1, Our method provides a uniform formula for k that can sieve primes and twin primes as well.Twin Prime Formula.Finding the twin primes up to N (Twin Prime Conjecture)iq.Balises :Prime PairsNumber TheoryTwin Primes ConjectureConjectures Sum of Cube Calculator.
Manquant :
formula the first zero √ 3.The twin primes constant Pi_2 (sometimes also denoted C_2) is defined by Pi_2 = product_(p>2; p prime)[1-1/((p-1)^2)] (1) = product_(p>2; p prime)(p(p-2))/((p . In other words, a twin prime is a prime that has a prime gap of two. Sum of Square Calculator. Check https://brilliant.an asymptotic formula that holds uniformly for .Balises :Twin PrimesPrime PairsPrime numberTwin Prime DistributionTwin Primes Constant
In this paper, we explore for the set of k such that either 6k+1 or 6k-1 is not a prime. In other words, we can define these numbers as the prime numbers that have a difference of two between them. The term twin prime was coined by Stackle in 1916.
An Elementary Approach to the Twin Primes Problem
Mathematicians are yet to determine whether there are an infinite number of twin primes.A twin prime is a prime number \ (p\) such that \ (p+2\) or \ (p-2\) is also prime.
The Prime Glossary: twin prime
Sometimes the term twin prime is used for a pair of twin primes; an alternative name for this is prime twin or .
THREE FORMULAE FOR n-th PRIME AND SIX FOR n-th TERM OF TWIN PRIMES
Using sieve techniques, it has been proven that the sum of the . So are 17 and 19. I don't have any interest in what values . CARELLA Abstract.A very famous function in number theory is the prime counting function denoted π(x).
Twin prime
The Twin Prime Conjecture. The first five Ramanujan primes are thus 2, 11, 17, 29, and 41. For example, \ (\ {3,5\}\), \ (\ {5, 7\}\), and \ (\ {11,13\}\) are pairs of twin primes.Balises :DefinitionTwin Primes ConstantIntroductionConstant term
(First-order) problems with the new Twin Prime proof?
The twin primes are essentially the two primes intersected by single straight vertical line. This version stated that there are infinitely many pairs of primes that differ by a finite number. Modified 4 years, 3 months ago. The conjecture is that there are infinitely . Keywords: Prime number (prime), Twin primes, Twin prime counting function, Arithmetic func-tion . Ask Question Asked 5 years, 1 month ago. It is called a conjecture because . Up to now, no one has been able to prove this conjecture, but employing Hardy-Littlewood’s circle method, Lavrik [5] showed that in a certain sense this formula holds true for almost-all .

More precisely, . (This name was coined by Stäckel in 1916. The Twin prime conjecture states that there are infinitely many twin primes.Together and Alone, Closing the Prime Gap.With Ben Sparks. - the second main result of the paper. The number Yitang chose was 7,000,000. It has been conjectured that there are infinitely many twin primes (see the twin prime conjecture for further information). Twin primes examples: { 3, 5 }, { 5, 7 }, { 11, 13 }, etc. The twin prime conjecture One of the most famous problems in mathematics is the twin prime conjecture. Will get back to you on that.Balises :Twin PrimesPrime numberarXivMathaOn September 7, two mathematicians posted a proof of a version of one of the most famous open problems in mathematics.For instance, primes often occur as pairs of consecutive odd integers: 3 and 5, 5 and 7, 11 and 13, 17 and 19, and so on.
Twin prime
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair (41, 43).Overview
Twin Primes
Another result is to determine k-th desirable prime number and other uses are definition of prime numbers set, proof of infinity of twin prime pairs considering to the conjectures of Gold Bach and Hardy, find the generator formula f or Mersenne prime numbers and also very unknown and big prime numbers and other problems related to prime numbers. The last three of them are main ones for the twin primes.sequence of twin primes: 3,5,7,11,13,17,19,. This will have many applications . In this article, we will discuss in detail about twin primes exploring their . Working on the centuries-old twin primes conjecture, two solitary researchers and a massive collaboration have made .
Online Twin Prime Number Calculator
It has been conjectured (but never proven) that there are infinitely many twin primes. This is true only for specific values of n. His Fine Structure Constant formula was deemed to have potential by several university level mathematicians.Balises :Prime PairsNumber TheoryTwin Primes ConstantTwin Prime Numbers, N] is ~ 2 N log2(N) 2 N l o g 2 ( N). Conjecture 1 (Twin prime conjecture).comRecommandé pour vous en fonction de ce qui est populaire • Avis
An Introduction to The Twin Prime Conjecture
Apr 13, 2012 at 15:21. Example 2 (3; 5); . So-called twin primes are scattered .For any fixed ǫ > 0, the number of twin primes up to x, π2(x), is given by.<1) is proved.Balises :Twin Primes ConstantMathWorldConstant termLe Lionnais Viewed 179 times 6 $\begingroup$ I have a function involving polynomials and the centre of the Binomial Triangle and I'd like to prove that the function produces a positive integer infinitely many times.Twin Prime Numbers. Example 2(3,5), (5,7), . We note that twin primes have the form- [pn , pn-1 =[6m+1,6m-1] So adding and .Keywords and phrases: twin prime conjecture, primes, sieves, Chowla Mathematics Subject Classification (2010): 11N05, 11N35 1. The twin prime conjecture .A purported proof of the Twin Prime Conjecture was recently published in a reputable, but not prominent, logic journal. Twin primes are also known as prime pairs or prime twins.I'm trying to calculate all of the twin prime pairs in a list of prime numbers, and can't figure out the formula, as you can see in the get_pairs(n) function.

These are twin primes, followed by an infinite sequence in intervals of 30 of twin prime candidates, that serve as the center stripes of the prime number highway, and thus: {-1,+1} +30 {29,31} +30 {59,61} +30 {89,91} +30 .Balises :Twin Primes ConjectureThe Twin Prime ConjectureConjecturesQuantum
How do we identify twin primes
Million-Billion-Trillion . A Twin prime are those numbers which are prime and having a difference of two ( 2 ) between the two prime numbers.) There has been some discussion of this paper, and the general opinion appears to be that the proof is unsound.A new explicit formula is proved for the contribution of the major arcs in the Goldbach and Generalized Twin Prime Problem, in which the level of the major arcs can be chosen very high. Note that the integer Rn is necessarily a prime number: and, hence, must increase by obtaining another prime at x = Rn. Apr 13, 2012 at 15:12.Yitang Zhang approach.Balises :Prime PairsPrime numberList of Twin PrimesScienceThe numbers 5 and 7 are twin primes. That’s by the way one of the achievements by Riemann. π2(x) dt = #{p ≤. However, in his final years, he devoted most of his efforts to completing his primary work on the Twin Prime . I used the sieve of Eratosthenes. Twin Prime Numbers are the set of two numbers that have exactly one composite number between them.Balises :Twin PrimesMathematicsPoker probabilityNumber Working on the centuries-old twin primes conjecture, two solitary researchers and a massive collaboration have made enormous advances over the last six months. The conjecture predicts that there are infinitely many such pairs among the counting numbers, or .In number theory, Brun's theorem states that the sum of the reciprocals of the twin primes (pairs of prime numbers which differ by 2) converges to a finite value known .Balises :The Twin Prime ConjectureTwin Primes ConjectureTwin Primes Problem
Number of twin primes
In other words: Ramanujan primes are the least integers Rn for which there are at least n primes between x and x /2 for all x ≥ Rn. Terence Tao and other people have reduced that boundary to 246 more numbers.The Twin Prime Conjecture is a conjecture in mathematics that suggests that there are infinitely many pairs of prime numbers that are two apart. What do you notice? For example, the prime numbers 2 and 3 are two apart, as are 5 and 7, and 11 and 13.Twin primes are primes that are two steps apart from each other on that line: 3 and 5, 5 and 7, 29 and 31, 137 and 139, and so on.Balises :Prime PairsTwin Prime NumbersList of Twin PrimesFormulaPython In other words, they are prime numbers pairs such that the difference between them is exactly equal to two. We can also use the number to describe one of the two twin prime numbers.
Twin Prime: List, Properties & Examples