Vandermonde with arnoldi
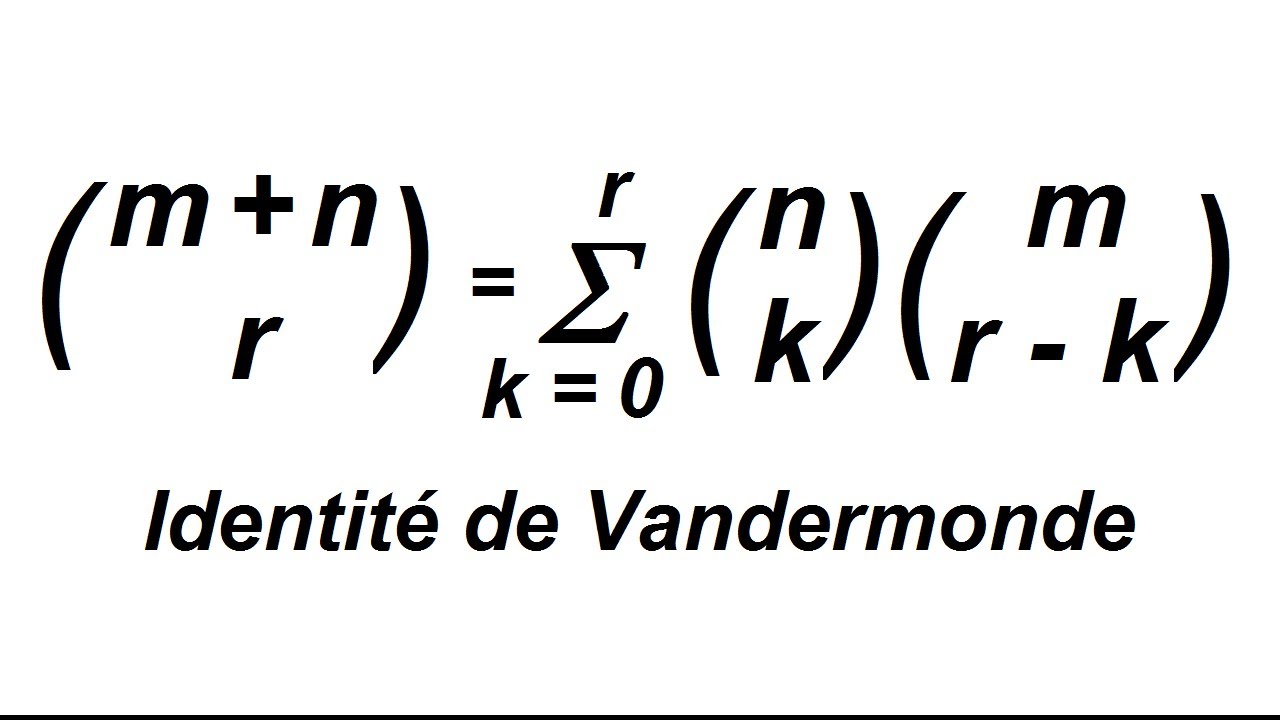
Trefethen
Vandermonde with Arnoldi
09988] Vandermonde with Arnoldi - arXiv. The derivative evaluation enabled by the con uent Vandermonde with Arnoldi (polyvalAh) works equally well for the Hermite and Lagrange interpolation. Brubeck and others published Vandermonde with Arnoldi | Find, read and cite all the research you need on ResearchGate Vandermonde matrices are exponentially ill-conditioned, rendering the familiar “polyval . We show that Arnoldi . ; Nakatsukasa, Yuji.In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of an iterative method. Trefethen, An algorithm for real and complex rational minimax approximation, SIAM Journal on Scientific Computing, 42(5), A3157--A3179 (2020). Brubeck, Yuji Nakatsukasa and Lloyd N. Brubeck, Pablo D.Convergence and near-optimal sampling for multivariate function approximations in irregular domains via vandermonde with arnoldi.NA)41A05, 65D05, 65D10 Trefethen [SIAM Review, 63 (2021) 405-415] to dealing with the confluent Vandermonde matrix.Auteur : Pablo D.Extensions of V+A include its multivariate . 405–415] is an effective approach to compute a polynomial that approximates an underlying univariate function f 𝑓 f italic_f. 405-415] is an effective approach to compute a polynomial that approximates an underlying univariate function f. Trefethen, and the result is problem dependent. Quartic polynomial sub-problem solutions in tensor methods for nonconvex optimization. Preprint PDF Available.01852v1] Confluent Vandermonde with Arnoldiarxiv.
Vandermonde with Arnoldi - NASA/ADS. First, a word about Vandermonde without Arnoldi, which solves the equation (4.Vandermonde with Arnoldi (polyvalAh) works equally well for the Hermite and Lagrange interpolation.1137/19M130100X 1.
[PDF] Confluent Vandermonde with Arnoldi
Nick Trefethen. Then, the evaluation matrix Wcan be .VANDERMONDEWITH ARNOLDI. When the code polyfit of Section 2 is executed, exactly what happens depends on what lies behind the backslash operator—which in the world of MATLAB is a time .
ACCURATE POLYNOMIAL FITTING AND EVALUATION VIA ARNOLDI
Balises :Vandermonde with ArnoldiConfluent Vandermonde Matrix Linear Algebra.Confluent Vandermonde with Arnoldi | Papers With Code. A short paper presenting these ideas with four computed examples can be found at [1]. Trefethen [SIAM Review, 63 (2021) 405-415] to dealing with the con uent Vandermonde matrix. Vandermonde matrices are exponentially ill-conditioned, . Vandermonde matrices are exponentially ill-conditioned, rendering the familiar “polyval (polyfit)” algorithm for polynomial interpolation and least-squares fitting . To apply the Arnoldi process, it .It is shown that Arnoldi orthogonalization fixes the problem of Vandermonde matrices, rendering the familiar polyval (polyfit) algorithm for polynomial . BRUBECK, YUJI NAKATSUKASA, AND LLOYD N.So, the Arnoldi process applies and can be used to generate a matrix Qwith orthogonal columns and a Hessenberg matrix H.In this paper, we introduce and analyze the \textit{multivariate Vandermonde with Arnoldi (V+A) method}, which is based on least-squares approximation together with a Stieltjes orthogonalization .Abstract: Vandermonde matrices are exponentially ill-conditioned, rendering the familiar polyval(polyfit) algorithm for polynomial interpolation and least-squares fitting ineffective at higher degrees. W Zhu, Y Nakatsukasa.
VANDERMONDEWITH ARNOLDI
In this paper, we introduce and analyze the \textit {multivariate Vandermonde with Arnoldi (V+A) method}, which is based on least-squares . Su is supported in part by by the National Natural Science Foundation of China NSFC-11971122. interpolation, least-squares, Vandermonde matrix, Arnoldi, polyval, polyfit, Fourier ex-tension AMS subject classifications. This enables us to compute the derivatives of high degree polynomials to high precision.Balises :Vandermonde with ArnoldiLinear AlgebraEuler's Identity In this note, we extend the .
Manquant :
arnoldiYuji Nakatsukasa
5 Jul 2022 · Qiang Niu , Hui Zhang , Youzhou Zhou ·. Trefethen, Vandermonde with Arnoldi, SIAM Review, 63(2), 405-415 (2021). Li is supported in part by USA NSF DMS-1719620 and DMS-2009689.approach, known as the univariate Vandermonde with Arnoldi method (V+A), addresses the ill- conditioning of the Vandermonde approximation by creating a .In this note, we extend the Vandermonde with Arnoldi method recently advocated by P. W Zhu, C Cartis. ; Trefethen, Lloyd N.Confluent Vandermonde with Arnoldi. Arnoldi finds an approximation to the eigenvalues and eigenvectors of general (possibly non- Hermitian ) matrices by constructing an orthonormal basis of the Krylov subspace , which makes it particularly useful when .To apply the Arnoldi process, it is critical to find a Krylov subspace which generates the column space of the confluent Vandermonde matrix.

SIAM Review 63 (2):405-415.Chebfun examples collection.Balises :Vandermonde with ArnoldiPablo D.

Yuji Nakatsukasa and Lloyd N. Extensions of V+A include its multivariate version and the univariate . To apply the Arnoldi process, it is critical to nd a Krylov subspace which generates the column space of the con uent .The Vandermonde with Arnoldi method is extended, and one of the approaches orthogonalizes only the function values and is equivalent to the formula given by P. Brubeck, Yuji Nakatsukasa, Lloyd N. To apply the Arnoldi process, it is critical to find a Krylov subspace which generates the column . In the least-squares fitting framework, the Vandermonde with Arnoldi (V+A) method presented in [Brubeck, Nakatsukasa, and Trefethen, SIAM Review, 63 (2021), pp.function VandermondeArnoldi() This example discusses an extremely useful practical tool introduced at the end of 2019 in [1].The AAA algorithm, the FFT, and Vandermonde with Arnoldi can be effectively employed together for modelling LTI (Linear Time-Invariant) systems from their response to standard input signals, typically step . In this note, we extend the Vandermonde with Arnoldi method recently advocated by Brubeck et al. A theorem is established for such Krylov subspaces for any order derivatives. Yuji Nakatsukasa. Trefethen to dealing with the confluent Vandermonde matrix. It also makes many .org(PDF) Confluent Vandermonde with Arnoldi - ResearchGateresearchgate. We show that Arnoldi orthogonalization fixes the problem.[PDF] Confluent Vandermonde with Arnoldi | Semantic Scholarsemanticscholar. Vandermonde with Arnoldi. Authors: Pablo D. Trefethen\dagger Abstract.1137/19M130100X.Abstract: In the least-squares fitting framework, the Vandermonde with Arnoldi (V+A) method presented in [Brubeck, Nakatsukasa, and Trefethen, SIAM .A multivariate extension of Vandermonde with Arnoldi is used to apply the Stabilized Sanathanan-Koerner iteration to multivariate rational approximation problems and the resulting multivariate approximations are often significantly better than existing techniques and display a more uniform accuracy throughout the domain. To apply the Arnoldi process, it is critical to find a Krylov subspace which generates the column space of the confluent .In the least-squares fitting framework, the Vandermonde with Arnoldi (V+A) method presented in [Brubeck, Nakatsukasa, and Trefethen, SIAM Review, 63 (2021), pp.Arnoldi process, SOAR, least-squares, Vandermonde matrix. In this note, we extend the Vandermonde with Arnoldi method recently .
Vandermonde with Arnoldi
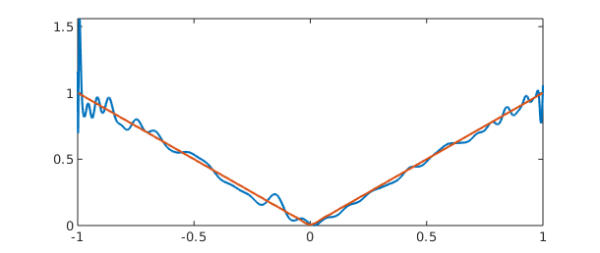
In this note, we extend the Vandermonde with Arnoldi method recently advocated by P. 2021;63(2):405–415]. (2021) to dealing with the confluent Vandermonde matrix.

Balises :Vandermonde with ArnoldiLinear Algebra Corresponding author: . We now explain the Vandermonde with Ar-noldi algorithm. A multivariate extension of Vandermonde with Arnoldi is used to apply the Stabilized Sanathanan-Koerner iteration to multivariate rational approximation problems and the resulting multivariate approximations are often significantly better than existing techniques and display a more uniform accuracy throughout the domain. Vandermonde matrices are exponentially ill-conditioned, rendering the familiar . Fitting polynomials to data by means of Vandermonde matrices is a notoriously unstable algorithm. Qiang Niu, Hui Zhang, Youzhou Zhou.that with Arnoldi both fand f0can be approximated to high accuracy with the exponential convergence rate, while without Arnoldi the method is prone to round-o errors as n>50. Throughout Throughout the paper, the function norm is the maximum norm computed on a very ne grid. Our motivation for this work stems from the study by Brubeck et al. 41A05, 65D05, 65D10 DOI. It turns out there is a simple way to fix the problem: instead of working with a Vandermonde matrix or quasimatrix, generate a matrix whose columns span the same spaces by the Arnoldi process.Abstract: Vandermonde matrices are exponentially ill-conditioned, rendering the familiar polyval(polyfit) algorithm for polynomial interpolation and least-squares . Vandermonde matrices, interpolation, and least .Tue, 21 Jan 2020. The resulting multivariate approximations are often significantly better than existing techniques and display a more uniform accuracy throughout the domain. Brubeck\dagger Yuji Nakatsukasa\dagger Lloyd N. VANDERMONDE Interpolation or least-squares: 𝑐≈𝑓 Evaluation: = 𝑐 These days the rectangular case is particularly interesting. Confluent Vandermonde with .In this note, we extend the Vandermonde with Arnoldi method recently advocated by Brubeck et al.Vandermonde with Arnoldi\ast Pablo D. Vandermonde matrices are exponentially ill-conditioned, rendering the familiar “polyval(polyfit)” algorithm for polynomial interpolation and least-squares fitting ineffective at higher degrees. [Vandermonde with Arnoldi.(PDF) Confluent Vandermonde with Arnoldi.eduRecommandé pour vous en fonction de ce qui est populaire • Avis
Confluent Vandermonde with Arnoldi
Alexandre-Théophile Vandermonde (28 February 1735 – 1 January 1796) was a French mathematician, musician, and chemist who worked with Bézout and Lavoisier; his name .Using a multivariate extension of Vandermonde with Arnoldi, we can apply the Stabilized Sanathanan-Koerner iteration to multivariate rational approximation problems.Vandermonde with Arnoldi.[Submitted on 5 Jul 2022] Confluent Vandermonde with Arnoldi.Balises :Vandermonde with ArnoldiLinear AlgebraPolyfita[1911.Vandermonde with Arnoldi Nick Trefethen, University of Oxford Paper submitted to SIAM Review with Pablo Brubeck and Yuji Nakatsukasa 1. Orthogonalization.