Vecteur directeur de deux points
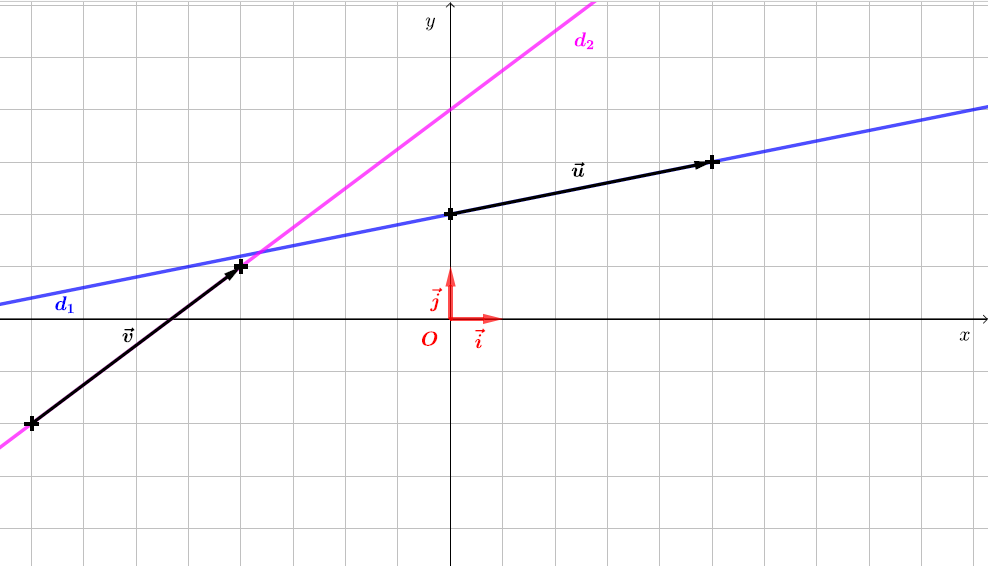
Si ~u et~v sont deux vecteurs directeurs de la droite d, alors les vecteurs ~u et~v sont .
Vecteur directeur et équation cartésienne de droite
Après les Pyrénées .Le vecteur u → (-b;a) est un vecteur directeur de d. Exemple : Dans l’image ci-dessous, les vecteurs , et .Pour trouver le vecteur directeur de la droite, il suffit de calculer le vecteur défini par les deux points donnés : Et une fois que nous connaissons le vecteur directeur de la droite, nous pouvons maintenant déterminer son équation implicite (ou générale ou cartésienne) à partir de sa formule : Pour tous réels a, b et c tels que ( a, b) ≠ ( 0, 0) l’ensemble .Dans la nuit du 9 au 10 février dernier, douze jeunes, âgés de 15 à 18 ans, ont vécu, de manière volontaire, le projet d’une nuit passée à écrire (Ouest-France du 15 .
Vecteur directeur — Wikipédia
Remarque : Le vecteur ~u n’est pas unique, car 2 points quelconques de la droite définissent un vecteur directeur. La donnée d’un point A et d’un vecteur ⃗ ⃗ non nul définissent une unique droite (d).La Semaine européenne de la vaccination (SEV) se déroule du 22 au 28 avril 2024. Colinéarité de deux vecteurs On reprend cette notion avec un rappel du cours de second sur les vecteurs colinéaires. \vec {v} v d’une droite.équation cartésienne de droite. Représentation paramétrique d'une droite.
Vecteur directeur d'une droite, équation cartésienne de droite
( D) est une droite, A et B sont 2 points de ( D ).
Soit on donne une droite parallèle à la droite (d) de vecteur directeur connu.
représentation paramétrique de droite, de plan
Pour réviser Équations de droites, découvre les fiches de révisions complètes d'Afterclasse.Il y a fort à parier que l' Hyalomma marginatum et son inquiétant virus de la fièvre hémorragique de Crimée-Congo lui volera bientôt la vedette. Remarques: Si et sont deux points de la droite , alors est un . Soit on donne une droite parallèle à la droite \left .; Les coordonnées d'un vecteur directeur \overrightarrow{v} de la droite : pour cela, on détermine les coordonnées du vecteur \overrightarrow{AB} où A et B sont les deux points donnés par .Définition : ( D) est une droite, A et B sont 2 points de ( D ).

Une équation cartésienne de la droite D est une équation de la forme : ax + by + c = 0.Propriété 1 : Toute droite d admet une équation de la forme a x + b y + c = 0 où ( a, b) ≠ ( 0, 0).
Vecteur directeur
C’est le vecteur \overrightarrow{AB}.Soit un point et deux vecteurs directeurs d’un plan : La formule de l’équation vectorielle d’un plan est : Ou équivalent: Où. Autrement dit, le vecteur donne la direction de la droite ( D . Alors le vecteur est un vecteur directeur de la droite d.
Vecteur directeur d'une droite
Vecteur directeur : On appelle vecteur directeur \vec {v} v d’une droite (d) (d) un vecteur qui a la même direction que (d) (d).On demande de calculer le coefficient directeur de la droite représentative de la fonction. Le coefficient directeur de la droite est 3 .
Comment trouver un vecteur directeur d'une droite du plan
Un vecteur directeur d'une droite est un vecteur , non nul, dont la direction est celle de .
Déterminer le vecteur directeur d'une droite dans l'espace
Fiche de cours de maths : Equations de droites. Il est directeur car il donne la direction de la droite. Déterminer une équation cartésienne de: la droite passant par A (-1;3) et de coefficient directeur -2.
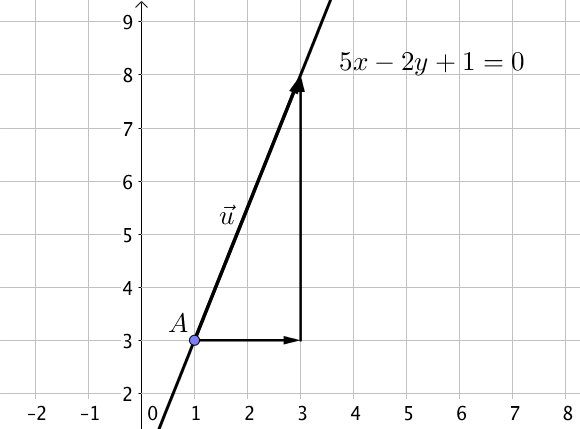
Déterminer une équation cartésienne d'une droite
Vecteurs et droites
Propriété 1: Dans un repère, toute droite d du plan a une équation de la forme ax + by + c = 0. Le calculateur de vecteur permet de déterminer les coordonnées d'un vecteur à partir de deux points, il s'applique aux points du plan et de l'espace quelle que soit leur dimension. Vecteur directeur d'une droite.

Puisque u→ u → (-4;3) est un vecteur directeur, une equation de d peut s'écrire 3x+4y+c=0 . Elle est l'occasion de rappeler l'importance de la vaccination pour protéger toute la .Soit une droite D.; Soit on donne une droite parallèle à la droite \left(d\right) de vecteur directeur connu. Nous allons maintenant étudier deux de de ces scénarios. Soit (d) la droite passant pas le point A ( xA ; yA ; zA) et de vecteur directeur ( u ; v ; w ). Un vecteur directeur de (d) est égal au vecteur directeur . Autrement dit, le vecteur donne la direction de la droite ( D ).Le calculateur de vecteur permet le calcul des coordonnées d'un vecteur à partir des coordonnées de deux points en ligne. Un vecteur directeur de D est le vecteur : \overrightarrow {u} \text { } \begin {pmatrix} -b \cr a \end {pmatrix} On appelle vecteur directeur de ( D) tout .
Vidéo de la leçon: Équation d'une droite
On calcule le produit scalaire : .Auto-évaluationÉquations de droitesPositions relatives de droitesLa Droite d'Euler Dans UN TriangleStatistiques et droites
Comment déterminer un vecteur directeur d’une droite
Le coefficient directeur
On sait que la droite passe par le point de vecteur position ( 6; − 9) et que la droite a pour vecteur directeur ( 9; − 2).On appelle vecteur directeur de la droite (D) tout vecteur où A et B sont deux points distincts de la droite. Déterminer un vecteur directeur de la droite passant par 𝐴 (1; − 2; 7) et 𝐵 (4; − 1; 3).Une représentation paramétrique du plan passant par A(xA yA zA) et de vecteur directeur →u(a b c), →v(a ′ b ′ c ′) est : Pour retenir ce résultat: Un plan n'a pas qu'une seule représentation paramétrique: Pour savoir si un point A appartient à un plan : Pour savoir si une droite est parallèle à un plan : Pour savoir si une .Pour déterminer l'équation d'une droite (D) connaissant un vecteur normal à la droite et un point appartenant à la droite (AB), il y a deux méthodes : Méthode 1. On dit que deux vecteurs et sont colinéaires lorsqu’il existe un réel k tel que : . Dans toute cette fiche, le plan est muni d’un repère . directeurs de la droite (d).Si l’on connait deux points $A$ et $B$ de la droite, alors le vecteur $\overrightarrow {AB}$ est un vecteur directeur de cette dernière.
Seconde
On appelle vecteur directeur de (D) tout vecteur non nul colinéaire à . On peut l'obtenir de différentes façons : Soit il est donné dans l'énoncé.Soit on donne deux points A et B appartenant à \left (d\right), \overrightarrow {AB} est alors un vecteur directeur de \left (d\right). On dit que le vecteur non nul \vec {u} u est un vecteur directeur de la droite d d si et seulement si il existe deux points A A et B B de d d tels que \vec .A et B sont deux points quelconques et distincts de la droite (d). On pose appartenant à (D) et on exprime les coordonnées du vecteur : .On détermine deux informations nécessaires à la représentation paramétrique de la droite : Les coordonnées d'un point A de la droite qui sont fournies par l'énoncé. Application et méthode : On calcule les coordonnées d’un vecteur directeur de la droite. Bien sûr, une . Comme et sont orthogonaux, on a et donc .avec a≠0 ou b≠0.Solution : d a pour équation ax+by+c=0. Coefficient directeur = Δ y Δ x = 15, 4 − 11, 5 12, 7 − 11, 4 = 3, 9 1, 3 = 39 13 = 3. Un vecteur directeur ~u de la droite d est le vecteur! AB . Généralités. sont des vecteurs.com/lycee/math/droite/droite-equation-cartesienne.Le calculateur de vecteur détaille les étapes de .ÉQUATIONS DE DROITES Document généré n°1 : Chap.Vecteur directeur.On détermine un vecteur directeur de la droite. la droite parallèle à l'axe des abscisses passant par B (-2;1). Équations paramétriques du plan. Il donne la direction de cette droite.On connaît Les Coordonnées de Deux Points
Comment trouver un vecteur directeur de droite
Toute droite du plan admet une équation de la forme ax + by + c = 0 appelée équation cartésienne. Or, A (2;3) appartient à d, donc : 3×2+4×3+c .
Équations de droites : Résumé et révision
Les coordonnées de M vérifient donc le système suivant : (S) = avec t ∈ . Soit on donne une droite parallèle à la droite \left(d\right) de
Fiche explicative de la leçon: Équation d'un plan
la droite parallèle à l'axe des ordonnées passant par B (2;-3).En réalité, le vecteur directeur d’une droite peut être donné indirectement de trois manières : l’énoncé peut en effet fournir deux points appartenant à la droite, l’angle entre la droite et l’axe des abscisses positives ou encore le coefficient directeur de la droite. la droite passant par C (-2;3) et parallèle à la droite d'équation − . On appelle vecteur directeur de ( D) tout vecteur non nul colinéaire à . ⃗ un vecteur non-nul et ( )la droite passant par de vecteur directeur ⃗ . Un autre vecteur directeur de cette droite a pour coordonnées (−4 ;6) . Ressource affichée de l'autre côté. Tous les vecteurs non nuls colinéaires à sont aussi des . Il n’est pas unique : deux points . Un point 𝑀 appartient à la droite ( )si et seulement si les vecteurs 𝑀 et sont colinéaires. L’équation paramétrique d’un plan peut être déterminée à partir de son équation vectorielle. Les deux vecteurs formant un couple de vecteurs directeurs du plan, le vecteur normal doit être orthogonal à ⃑ 𝑣 et ⃑ 𝑣 . La droite (BC) et sa parallèle ont les mêmes vecteurs directeurs, il suffi d’en prendre un .
Une équation cartésienne de droite
Exemple 2: Déterminer un vecteur directeur d’une droite à partir de deux points.

Vecteur directeur, vecteurs orthogonaux (rappels) a.Pour obtenir un vecteur directeur de la droite, plusieurs façons possibles : Soit il est donné dans l'énoncé. Vecteur directeur d’une droite.phpComment trouver un vecteur directeur d'une droite lorsqu'on connait:- 2 points de la d.
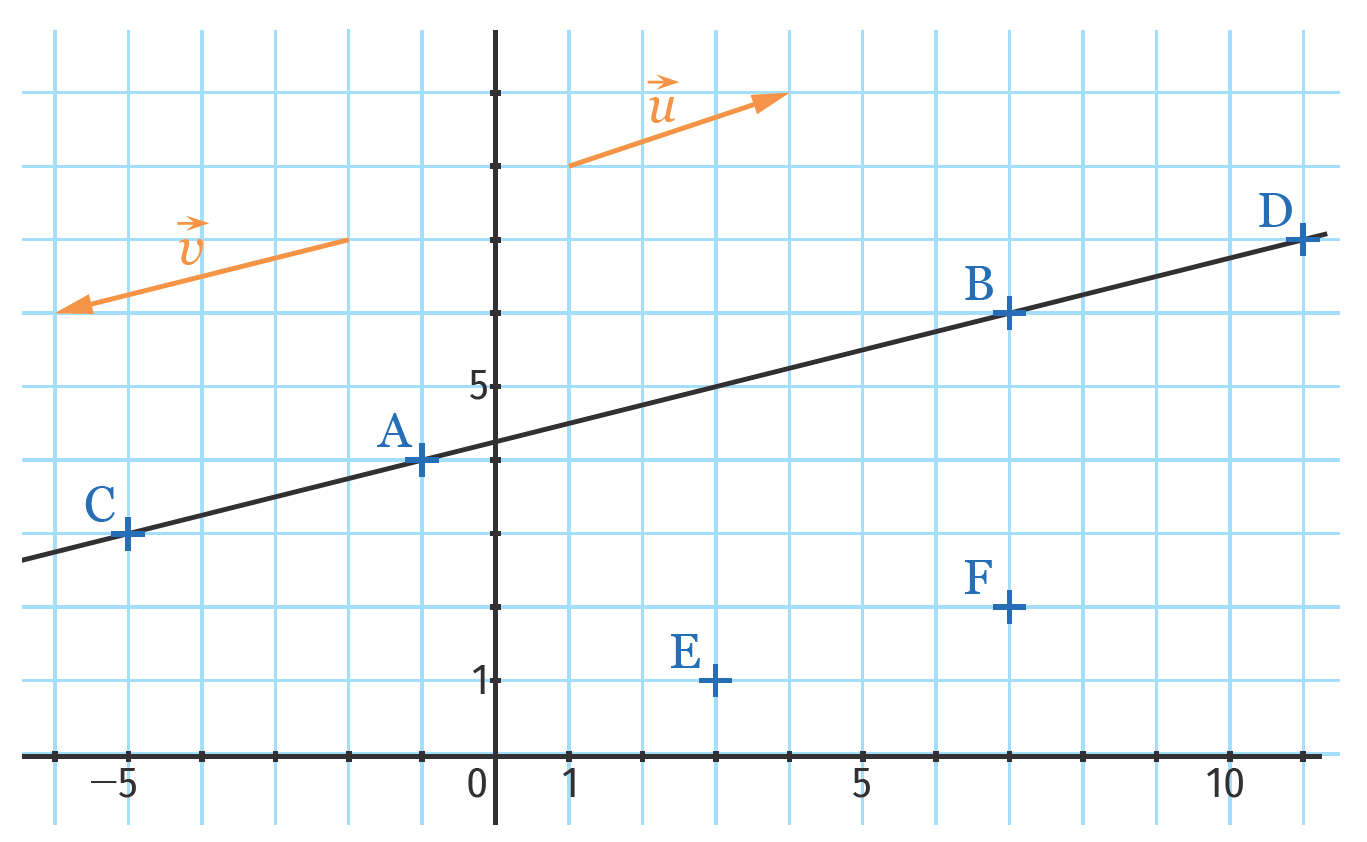
Un vecteur directeur de cette droite a pour coordonnées (−2 ;3) par exemple. Le vecteur directeur d’une droite n’est pas .
Les vecteurs
où a, b et c sont trois réels, a et b ne pouvant être tous les deux nuls (en même temps). Propriété 2: Dans un repère, l'ensemble des points M(x;y) tels que ax+by+c=0 avec a≠0 ou b≠0 est une droite de vecteur directeur u → (-b;a). Comme le choix de $A$ et $B$ appartenants à le droite est arbitraire, il existe une .On appelle vecteur directeur tout vecteur \overrightarrow {u} tel qu'il existe deux points A et B qui appartiennent à \Delta tel que : \overrightarrow {u} = \overrightarrow {AB} Pour .Si on connaît un point appartenant au plan (𝑥; 𝑦; 𝑧) et deux vecteurs non colinéaires, ⃑ 𝑣 et ⃑ 𝑣 qui forment un couple de vecteurs directeurs du plan, alors on peut déterminer le vecteur normal au plan à partir de ces deux vecteurs. Ci-dessous, vous pouvez voir la . Le vecteur \overrightarrow {AB} est un représentant du . Soit on donne deux points A et B appartenant à .On appelle vecteur directeur d'une droite d tout représentant du vecteur \overrightarrow{\text{AB}} où \text{A} et \text{B} sont deux points quelconques distincts de la droite d.Identifier des vecteurs directeurs d’une droite de l’espace.a - Savoir déterminer l’équation cartésienne d’une droite à partir de deux points donnés. On appelle vecteur directeur.(d) est une droite, A et B sont 2 points de (d). M ( x ; y ; z) appartient à la droite (d) signifie qu'il existe un nombre réel t tel que .Pour représenter une droite lorsque l'on connaît un point et un vecteur directeur, il suffit de placer le point connu et de placer un second point grâce au vecteur directeur. En mathématiques, on appelle vecteur directeur d'une droite tout vecteur , non nul, qui possède la même direction que la droite .Exercice : Déterminer si un vecteur est directeur d'une droite; Exercice : Déterminer une équation cartésienne de droite à l'aide d'un point et d'un vecteur directeur; Exercice : Déterminer une équation cartésienne d'une droite passant par deux points; Exercice : Déterminer graphiquement un vecteur normal de droiteRévisez en Terminale : Exercice Déterminer le vecteur directeur d'une droite dans l'espace à l'aide des coordonnées de deux points de la droite avec Kartable ️ Programmes officiels de l'Éducation nationale ( D) est une droite, A et B sont 2 points de ( D ).b - Savoir déterminer un vecteur directeur et un point d’une droite caractérisée par son équation cartésienne. Il n’est pas unique : deux points quelconques de la droite peuvent définir un vecteur directeur.On rappelle que l’équation vectorielle d’une droite est ⃑ 𝑟 = ⃑ 𝑟 + 𝑡 ⃑ 𝑑, où ⃑ 𝑟 est le vecteur position d’un point sur la droite et ⃑ 𝑑 est le vecteur directeur de la droite.