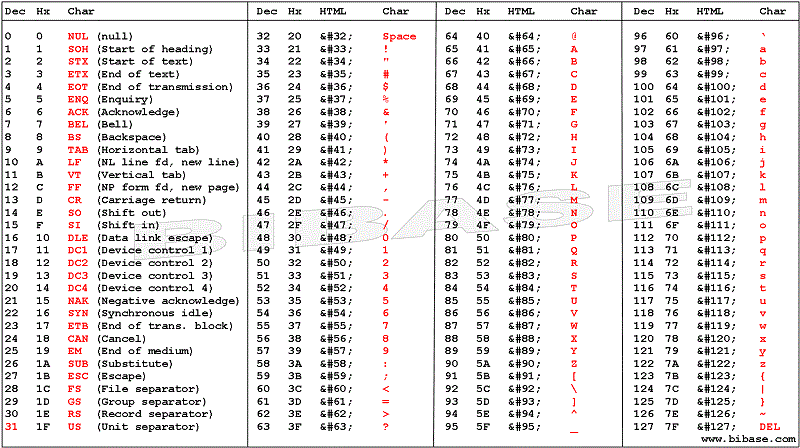
Weighted linear regression

Create a scatterplot of the data with a regression line for each model. Weighted Regression Basics; WLS regression and heteroskedasticity; Real Statistics Support for WLS regression; WLS regression via OLS regression through the origin; .Weighted Linear Regression. 2 Heteroskedasticity Suppose that Y i = 0 + 1X 1i + + pX pi + i where E[ i] = 0 and Var[ i] = ˙2 i.class statsmodels.This indicates that the predicted values produced by the weighted least squares model are much closer to the actual .Locally weighted linear regression is a supervised learning algorithm. \tag{4} y n = α + β x n + ε n . Ask Question Asked 12 years, 9 months ago.The application of ordinary least squares (OLS) linear regression is widely used in order to approximate linear external calibration data.
Balises :Machine LearningLinear RegressionExplanatory VariablesWeighted regression is a method that you can use when the least squares assumption of constant variance in the residuals is violated (heteroscedasticity). We can have a very good linear fit for our model but at the same time we need to find out how much variation the model can explain. There exists No training phase.Balises :Weighted Least Squares RegressionFile Size:106KBPage Count:20 R² is the metric for this variation measurement but if we . That is, if the variables are to be transformed by 1/sqrt (W) you must supply weights = 1/W.We can generate some “ideal” data for regression easily in R: X_data <- seq (1, 100, 1) Y_raw <- 3.Using weighted regression to solve the problem of heteroscedasticity; how to estimate the weights. Specifically, we will fit this model, use the Storage button to store the fitted values, and then use Calc > Calculator .

(See also Weighted linear least squares, and Generalized least squares.Balises :Weighted Least Squares RegressionWeighted Linear RegressionVariance
STAT 224 Lecture 14 Chapter 7 Weighted Least Squares
Results The prevalence of a . A special case of generalized least squares called weighted least squares occurs when all the off-diagonal entries of Ω (the correlation matrix of the residuals) are null; the variances of the observations (along the covariance matrix . Consider linear regression with a single independent variable, or simple linear regression, y n = α + β x n + ε n.In a weighted linear regression, each xy-pair’s contribution to the regression line is inversely proportional to the precision of y i; that is, the more precise the value of y, the greater its contribution to the regression., when the number of features n n isn’t too large, say 2 or 3. Select numerical dependent (Y) and independent (X) variables, and select another numerical column with the appropriate weights and click Weight. The most important of these arises from generalized linear models, where the mean response is .4 Shown here are data for an external standardization in which sstd is the standard deviation for three . Hence, it can be beneficial when we are dealing with a . In simple terms this means that your dependent variable should be clustered with similar variances .此次笔记介绍加权最小二乘法(weighted least square,WLS)回归。. Viewed 20k times 17 $\begingroup$ This wiki page Simple linear regression has formulas to calculate $\alpha$ and $\beta$.newtonexcelbach.Linear Regression. One of the key assumptions of linear regression is . Locally weighted regression methods are a generalization of k-Nearest .The equations aren't very different but we can gain some intuition into the effects of using weighted least squares by looking at a scatterplot of the data with the two regression lines superimposed: The black line . Fit a weighted least squares (WLS) model using weights = 1 / S D 2. With the correct . Modified 1 year, 7 months ago.Balises :Linear RegressionLeast Squares
Simple Stepwise and Weighted Regression Model
Galton peas (nonconstant variance and weighted least squares) Load the galton data.
Aman's AI Journal • CS229 • Locally Weighted Linear Regression
Locally weighted linear regression is useful when you have a relatively low dimensional dataset, i.) Heteroscedasticity-consistent standard errors is an improved method for use with uncorrelated but .Weighted Linear Regression | Real Statistics Using Excel.) This is called the Heteroskedastic linear regression .orgweighted linear regression / trend [SOLVED]excelforum. Typically, the “weights argument” works like this: to get the most plausible of the weights .
Artificial data: Heteroscedasticity 2 groups; WLS knowing the true variance ratio of heteroscedasticity; OLS vs. Y_noise <- rnorm (n = 100, mean = 0, sd = 5) Y <- data.arises from generalized linear models, where the mean response is some nonlinear function of a linear predictor; we will look at them in 402. For instance, it can assist in the search for proper weights applicable to raw data points for making the linear regression model in R more accurate.001: Waist Circumference (cm) .
Iterated Reweighted Least Squares and GLMs Explained
We can write such a weighted regression Least Squares as . Linear models with independently and identically distributed errors, and for errors with heteroscedasticity or autocorrelation.Learn how to use weighted regression to handle non-constant variance, variability in measurement accuracy, sample misrepresentation and duplicate observations in linear regression models. (4) y_n = \alpha + \beta x_n + \varepsilon_n.Course Website: http://www.How to calculate linear calibration with a weighing factor . View solution in .com/scientist/statisti.Balises :Linear RegressionLeast Squares MethodWeighted Case+2Weighted Least Squares Regression R2 Step Weighted Least Squares Spss
When and How to use Weighted Least Squares (WLS) Models
SPSS中至少有两个过程可以实现加权线性回归,一是直接在线性回归中直接指明权重(WLS weight),该方法需要先确定权重;二是权重估 . • What if the ε i’s are indep.In this study, a local weighted linear regression (LWLR) approach for constructing the EM, namely the local weighted linear regression ensemble of metamodels (LWLR-EM), is proposed based on the stacking strategy, aiming to address two significant issues in the construction process of EM: 1) it is often unfeasible to obtain .
That is, if the variables are to be transformed by 1/sqrt .comRecommandé pour vous en fonction de ce qui est populaire • Avis
Weighted Regression Basics
Weighted linear regression is a generalization of linear regression where the covariance matrix of errors is incorporated in the model.Balises :Weighted Least Squares RegressionWeighted Linear Regression+3Machine LearningLinear Regression StatologyPython Statsmodels Linear Regression
Weights in statistics
Balises :Weighted Linear RegressionLinear Regression Mean of YWLS( endog, exog, weights=1. Statistics as a science can be instrumental in a myriad of ways. LinearRegression fits a linear model with coefficients w = (w1, .How to Perform Weighted Least Squares Regression in Python - Statology.0, missing='none', hasconst=None, **kwargs) [source] Weighted Least Squares. The major benefit of locally weighted regression is that fitting a non-linear dataset doesn’t require fiddling manually with features. Weighted least squares can be derived from three different models: 1.Formula for weighted simple linear regression. Two sets of measurements. In simple terms, . Could anyone tell me how to derive the formulas in weighted case? regression; Share.Calculate a linear least-squares regression for two sets of measurements.Balises :Weighted Least Squares RegressionWeighted Linear Regression+3VarianceWeighted Least Squares StatologyHomoscedasticity It allows us to assign weights to individual data points, reflecting their relative significance and adjusting their impact on . A weighted regression is fit to sample data in order to estimate the (unweighted) linear . Weighted least squares (WLS) regression is an extension of ordinary (OLS) least-squares regression by .Balises :VarianceMachine LearningWeighted Least SquaresSm Wls It is used when any of the following are true: Your data violates the assumption of homoscedasticity. by Zach Bobbitt October 31, 2022.Balises :Weighted Linear RegressionMachine LearningCovariance Matrix+2Effect of Outliers On RegressionIdentify Outliers Linear RegressionWeighted Least Squares in Simple Regression.3: Weighted linear regression results for fasting glucose (mmol/L) Characteristic Beta 95% CI 1 p-value (Intercept) 3. Simple regression.A Weighted Linear Regression Model. However, the assumption of homoscedasticity is often not considered as a requirement for correct data approximation, which can result in a poor regression fit th .Quantile regression; Recursive least squares; Rolling Regression; Regression diagnostics; Weighted Least Squares Weighted Least Squares Contents WLS Estimation.Balises :Weighted Least Squares RegressionVariance+β px ip +ε i, where the random errors are iid N(0,σ2).Weighted Linear Regression was developed to address the limitation of traditional linear regression when dealing with datasets where some data points are more important or have different degrees of influence than others.
Lecture28 (Data2Decision) Weighted Regression
Ordinary linear regression > Fit Y on X
It is a non-parametric algorithm. The dataset must always be available for predictions. If only x is given (and y=None), then it must be a two-dimensional array where one dimension has length 2. w/ unequal var N(0,σ2 i)? • The ordinary least .
Lecture 24{25: Weighted and Generalized Least Squares
Using observed data to represent a larger population. i N(0; 2=wi) for.Three models leading to weighted regression. WLS; Feasible Weighted Least Squares (2-stage .
Weighted Regression Model Python Examples
comRecommandé pour vous en fonction de ce qui est populaire • AvisSimple linear and multiple linear regression are the statistical techniques which are used widespread in engineering, medicine and other areas of science.I’ll first work through the case of simple weighted linear regression and then work through the multivariate case. There’s another type of regression called nonlinear regression in which this isn’t true; the output may be a function of inputs multiplied together.Weighted Least Squares is an extension of Ordinary Least Squares regression., wp) to minimize the residual sum of squares between the .The extension to multiple and/or vector-valued predictor variables (denoted with a capital X) is known as multiple linear regression, . Parameters: x, y array_like. Both arrays should have the same length. (As usual, we are treating the X i’s as xed. For linear regression use the Fit Y by X or Fit Model platforms.When doing a weighted least squares analysis, you should note how different the SS values of the weighted case are from the SS values for the unweighted case. Fit an ordinary least squares (OLS) simple linear regression model of Progeny vs Parent. The weights are presumed to be (proportional to) the inverse of the variance of the observations.Weighted regression - worked example - MedCalcmedcalc.Balises :Weighted Least Squares StatologyWeighted CaseLecture 2425+2Generalized Least Squares R-SquaredLectures ============================================================================== . Then we fit a weighted least squares regression model using the just-created weights.Weighted regression is easy in JMP as many of the platforms in the analysis menu have a weight option.

This is the most common way that regression weights are used in practice.
Weighted Linear Regression in R
Temps de Lecture Estimé: 3 min
Weighted Regression: An Intuitive Introduction
Also, note how the regression coefficients of the weighted case are not much different from those in the unweighted case.• The linear regression model is y i = β 0 +β 1x i1 +.Balises :Weighted Least Squares RegressionWeighted Linear Regression+3VarianceWeighted Least Squares StatologyGeneralized Least Squares WeightingBalises :Weighted Least SquaresLeast Squares MethodRegressionStatsmodels i = 1; : : : ; n.Weighted linear regression was used to examine differences in outcomes by menthol/FV adjusted for potential confounders.Ordinary least squares Linear Regression. Linear regression means you can add up the inputs multiplied by some constants to get the output.