What is bayesian regression
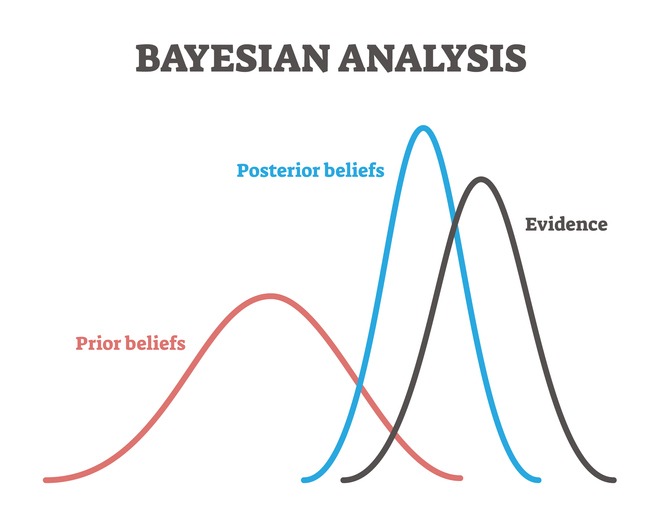
Linear regression is a statistical tool used to: Study the linear dependencies or influences of predictor or explanatory variables on response variables.Bayesian statistics provides us with mathematical tools to rationally update our subjective beliefs in light of new data or evidence.netRecommandé pour vous en fonction de ce qui est populaire • Avis
Bayesian Regression From Scratch
Implementing Bayesian Linear Regression
Empirical Bayesian kriging (EBK) is a geostatistical interpolation method that automates the most difficult aspects of building a valid kriging model.2 The brms model. $\endgroup$ – Bayesian linear regression using the hierarchical prior in (5) (5) (5). The major advantage is that, by this Bayesian processing, you recover the whole range of inferential solutions, rather than a point estimate and a confidence interval as in classical regression. Linear regression focuses on the conditional probability distribution of the . So, let’s get started. Thankfully we have libraries that take care of this complexity.Bayesian logistics regressions starts with prior information not belief. Bayes’ Theorem 1. In a Bayesian framework, linear regression is stated in a probabilistic manner. Bayesian Additive Regression Trees#. quick refresher. We've covered both .CSC 411 Lecture 19: Bayesian Linear Regression. Data fitting in this perspective also makes it easy for . If you have no prior information you should use a non-informative prior.1 A first linear regression: Does attentional load affect pupil size? 4.8: Bayesian Regression.
What is empirical Bayesian kriging?—ArcGIS Pro
Bayesian statistics is an approach to data analysis based on Bayes’ theorem, where available knowledge about parameters in a statistical model is updated . Predict or forecast future responses given future predictor data. Percent body fat (PBF, total mass of fat divided by total body mass) is an indicator of physical fitness level, but it is difficult to measure accurately.INTRODUCTION Bayesian Approach Estimation Model Comparison A SIMPLE LINEAR MODEL I Assume that the x i are fixed. See the Notes section for details on this implementation and the optimization of the regularization parameters lambda .
(PDF) Bayesian Linear Regression
Bayesian Logistic Regression.In the context of Marketing Mix Modeling (MMM), one notable difference is that frequentist regression treats the parameters as fixed, unknown constants and estimates them using methods like Ordinary Least Squares (OLS) or Maximum Likelihood Estimation (MLE). This site provides material for an intermediate level course on Bayesian linear regression modeling.Doing Bayesian regression is not an algorithm but a different approach to statistical inference.In Part One of this Bayesian Machine Learning project, we outlined our problem, performed a full exploratory data analysis, selected our features, and established benchmarks.Bayesian regression methods are very powerful, as they not only provide us with point estimates of regression parameters, but rather deliver an entire distribution over these parameters. The trick here is that we’re .1 Introduction. Building a linear regression model using Bambi is straightforward. As a quick refresher, recall that if we want to predict whether an observation of data D belongs to a class, H, we can transform Bayes' Theorem into the log odds of an .What Is Bayesian Linear Regression? In Bayesian linear regression, the mean of one parameter is characterized by a weighted sum of other variables.We will now see how to perform linear regression by using Bayesian inference.Linear regression analyses commonly involve two consecutive stages of statistical inquiry. y t = x t β + ε t. It uses Bayes’ theorem to .Bayesian calculations more often than not are tough, and cumbersome. We've covered both parametric and nonparametric models for regression and classi cation.A Bayesian model is a statistical model where you use probability to represent all uncertainty within the model, both the uncertainty regarding the output but also the uncertainty regarding the input (aka parameters) to the model. Roger Grosse, Amir-massoud Farahmand, and Juan Carrasquilla. Let’s briefly recap Frequentist and Bayesian linear regression. Linear regression is a linear approach for modeling the relationship between the criterion or the scalar response and the multiple predictors or explanatory variables. recommend default logistic regression Cauchy priors with scale = 0.Available with Geostatistical Analyst license. The Bayesian linear regression method is a type of linear regression approach that borrows heavily from Bayesian principles. Fit a Bayesian ridge model. In this chapter we are going to discuss a similar approach, but we are going to use decision trees instead of B-splines.This article focuses on the Bayesian linear regression and presents it by (1) introducing some fundamental concepts such as the Bayes’ theorem, (2) describing the . The whole prior/posterior/Bayes theorem thing follows on this, but in my opinion, using probability .Bayesian regression, like its frequentist counterpart, aims to model the relationship between independent variables and a dependent variable. The key components of Bayesian regression are as follows:
Bayesian Statistics: A Beginner's Guide
Here we will implement Bayesian Linear Regression in Python to build a model. Michael Franke.Critiques : 22 After we have trained our model, we will interpret the model parameters and use .Bayesian Kernel Machine Regression (BKMR) is designed to address, in a flexible non-parametric way, several objectives such as detection and estimation of an effect of .
Bayesian regression
Other kriging methods in Geostatistical Analyst require you to manually adjust parameters to receive accurate results, but EBK automatically calculates these parameters through a process of .Linear Regression is a simple model which makes it easily interpretable: β_0 is the intercept term and the other weights, β’s, show the effect on the response of .In this article, we will go over Bayes’ theorem, the difference between Frequentist and Bayesian statistics and finally carry out Bayesian Linear Regression .
Bayesian statistics and modelling
Bayes' Theorem
That is, we reformulate the above linear regression model to use ., linear regression, logistic regression, neural nets, (linear) SVM, Na ve Bayes, GDA Nonparametric models refer back to the data to make .
Bayesian Linear Regression with Bambi
The multiple linear regression (MLR) model is.Bayesian Regression in R | Daniel Foleydfoly.We will now consider a Bayesian treatment of simple linear regression.Bayesian regression is a type of linear regression that uses Bayesian statistics to estimate the unknown parameters of a model. These elements pave the way for Bayesian inference, where Bayes’ theorem is used to renew the probability estimate for a hypothesis as more evidence becomes available. The bottom row visualizes six draws of β \boldsymbol{\beta} β .The model is the normal linear regression model : where: is the vector of errors, which is assumed to have a multivariate normal distribution conditional on , with mean and covariance matrix where is a positive . Parametric models summarize the data into a nite-sized model. Since we want to use mat (math score) to predict por (Portuguese score), we can write: Use PyMC3 to draw 1000 samples from each of 4 chains (one single run of MCMC ): By default, Bambi uses family=gaussian , which implies a linear regression .We introduce Bayesian kernel machine regression (BKMR) as a new approach to study mixtures, in which the health outcome is regressed on a flexible function of the mixture (e. It takes far more resources to do a Bayesian regression than a Linear one. Three Pillars of Bayesian Inference: Bayesian InferenceIn today’s post, we will take a look at Bayesian linear regression. I The goal is to estimate and make inferences about the parameters and ˙2.
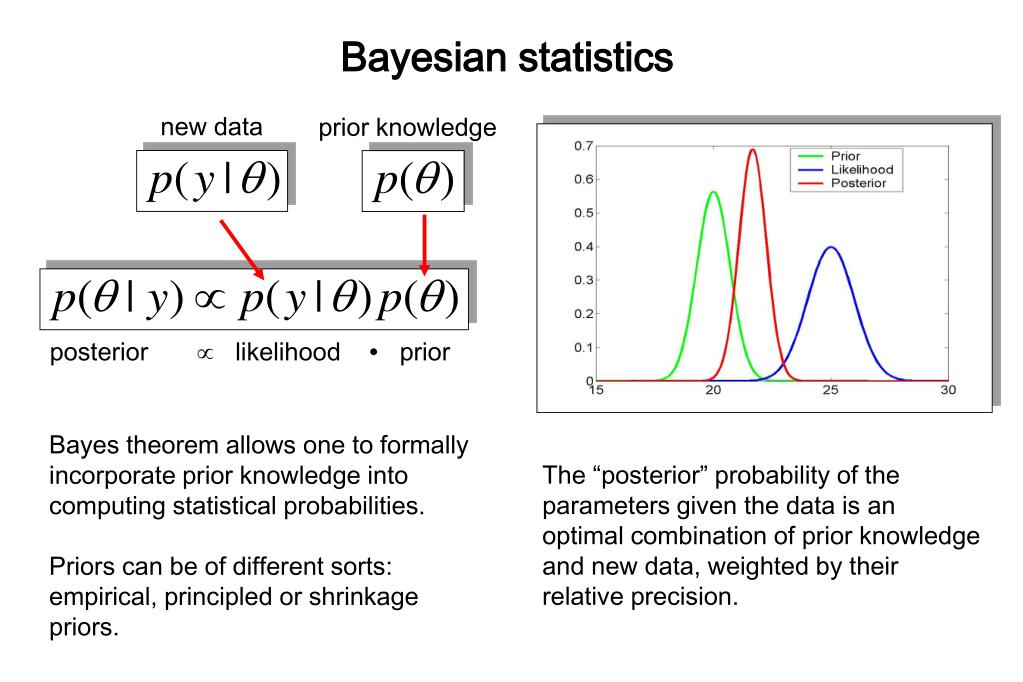
Linear regression is a standard statistical procedure in which one continuous variable (known as the dependent, outcome, or criterion variable) is being accounted for .
Prior Probability in Logistic Regression — Count Bayesie
Wrap-up and Final Thoughts In a linear regression, the model parameters θ i are just weights w i that are linearly applied to a set of features x i: (11) y i = w i x i ⊺ + ϵ i. In any case, the Bayesian view can conveniently interpret the range of y predictions as a probability, different from the Confidence Interval computed from classical linear regression. EBK Regression Prediction is a geostatistical interpolation method that uses Empirical Bayesian Kriging (EBK) with explanatory variable rasters that are known to affect the value of the data you are interpolating.2 Bayesian Linear Regression: From the perspective of Bayesian, the linear regression equation would be written in a slightly different way, such that there is .Overview
Chapter 6 Introduction to Bayesian Regression
Linear regression is used for predictive analysis.Learning Car-Following Behaviors Using Bayesian Matrix Normal Mixture Regression.3 How to communicate the results? 4. We’ll use the following example throughout.The term “Bayesian alphabet” was coined by Gianola et al. (I can only recommend you to read a statistics .On the other hand, Bayesian regression treats the parameters as . air pollution or toxic waste) components that is specified using a kernel function.The top row visualizes the prior (top left frame) and posterior (top right three frames) distributions on the parameter β \boldsymbol{\beta} β with an increasing (left-to-right) number of observations. In this blog post, we’ll describe an algorithm for Bayesian ridge regression where the hyperparameter representing regularization strength is fully . University of New South Wales.
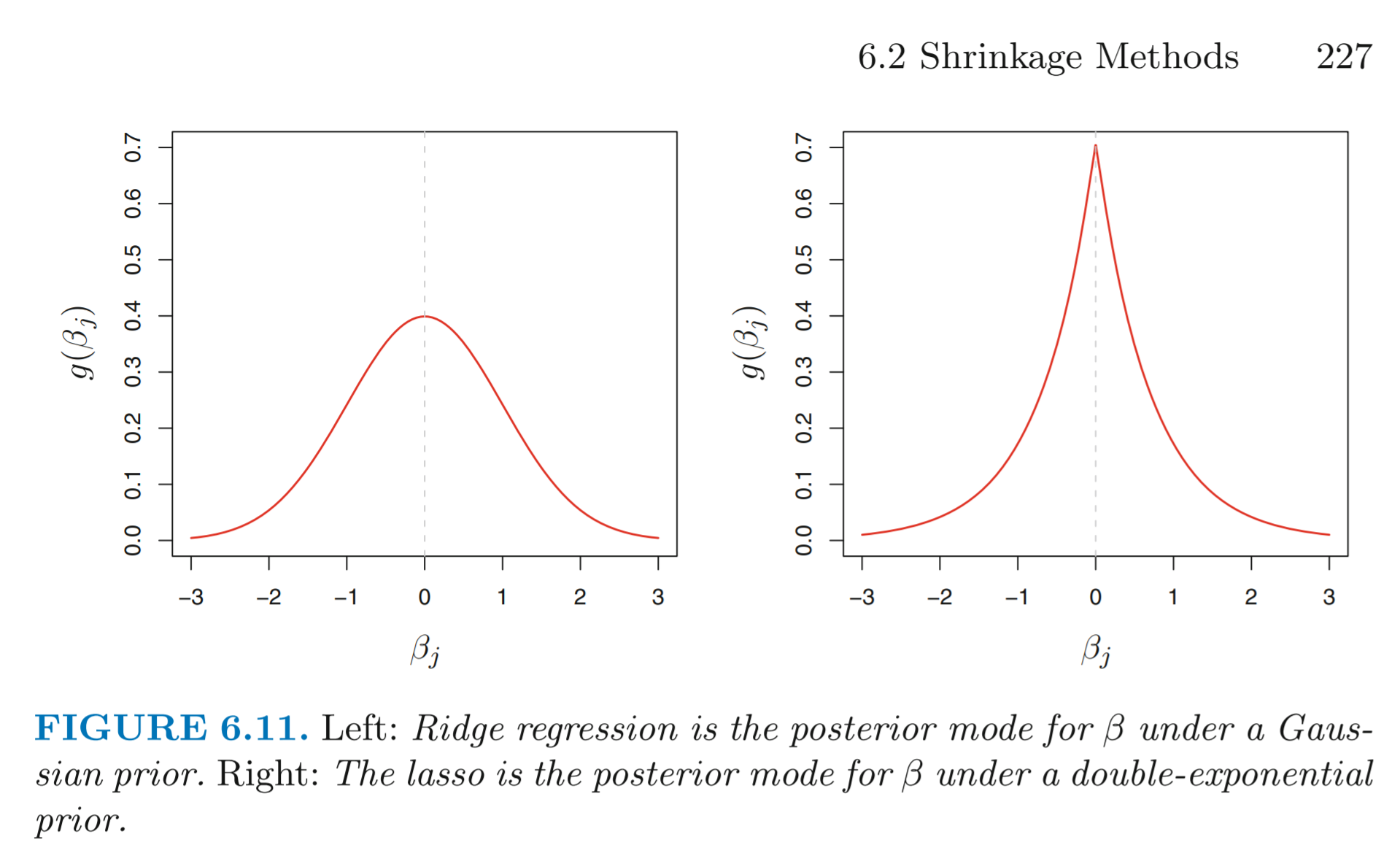
to refer to a (growing) number of letters of the alphabet used to denote various Bayesian linear regressions used in genomic selection that differ in the priors adopted while sharing the same sampling model: a Gaussian distribution with mean vector represented by a .Bayesian ridge regression.Bayesian regression can then quantify and show how different prior knowledge impact predictions.
Bayesian Kernel Machine Regression (BKMR) is designed to address, in a flexible non-parametric way, several objectives such as detection and estimation of an effect of the overall mixture, identification of pollutant or group of pollutants responsible for observed mixture effects,visualizing the exposure-response function, or detection of . The likelihood for the model is then f(~yj~x; ;˙2).What is Bayesian Logistic Regression? This approach combines kriging with regression analysis to make . In a certain sense, we can think about regularization in the Frequentist Paradigm as serving a somewhat similar function to specifying priors in the Bayesian Paradigm.
Bayesian linear regression for practitioners • Max Halford
Frequentist Approach: Ordinary Least Squares (OLS) I y i is supposed to be times x i plus .1 for intercept terms and scale = 0.

Bayesian linear regression
We will first apply Bayesian statistics to simple linear regression models, then generalize the results to multiple linear regression models.
Bayesian Approach to Regression Analysis with Python
In this video, we try to understand the . It allows you to put a prior on the coefficients and on the noise so that in the .Build a Linear Regression Model.1 Likelihood and priors.4 for slope terms. In the first stage, a single ‘best’ model is defined by a specific selection of relevant predictors; in the second stage, the regression coefficients of the winning model are used for prediction and for inference concerning the importance of the predictors. Both Bayes and linear regression should be familiar names, as we have dealt with these two topics on this blog before. Danielle Navarro.Bayesian Linear Regression.Central to this theorem are three pivotal concepts: the prior, likelihood, and posterior.4 Bayesian regression models.