Why is ssa not congruent
For example: (See Solving SSS Triangles to find out more) If three sides of one triangle are equal to three sides of another triangle .
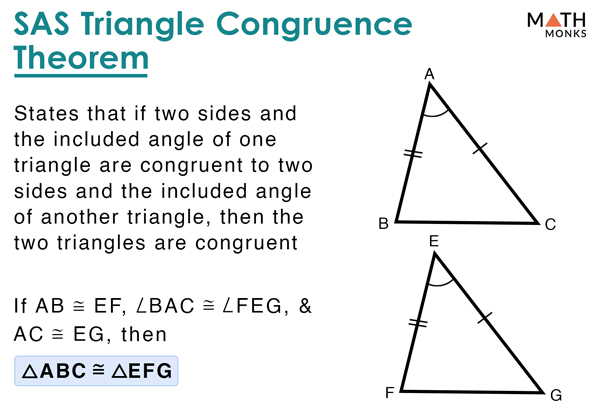
SSA Congruence Rule
Knowing only angle-angle-angle (AAA) does not work because it can produce similar but not congruent triangles.
Congruent Triangles - Why AAA doesn't work.When I deal with SSA in class, I refer to it, first, as a conjecture: that two triangles can be shown to be congruent if they each contain two pairs of corresponding, . Also for the sides marked with three lines. They have two sets of congruent sides and a non-included angle.Watch more videos on http://www.
If two triangles have two congruent sides and a congruent non included angle, then triangles are . SSS (side, side, side) SSS stands for side, side, side and means that we have two triangles with all three sides equal.
Solved Why is SSA (side, side, angle) congruence not
This is very similar to the ASA Postulate above because it also has two angles and a side.En savoir plus
How To Prove Triangles Congruent
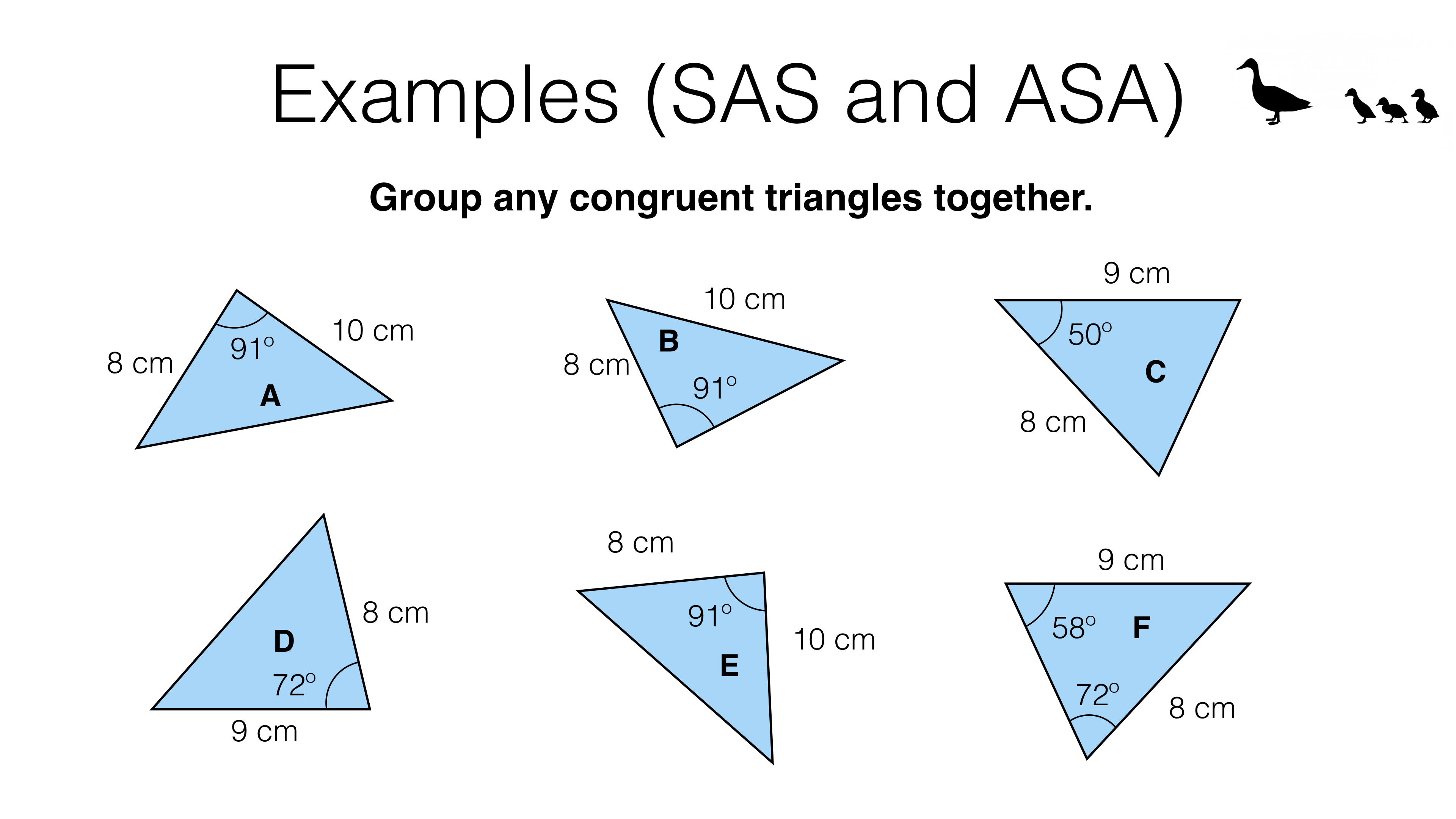
The angles marked with one arc are equal in size.
In this case you have to find the scale factor from 12 to 30 (what you have to multiply 12 by to get to 30), so that you can . In this video, we will learn how to prove that two triangles are congruent using either the side-side-side, side-angle-side, or the right-angle-hypotenuse-side criterion. SSA is valid if: the angle is a right angle.4K views 15 years ago. See SSA Side-Side-Angle condition: If two sides and a corresponding non-included angle of a triangle have the same length and measure, .comOn Triangle Congruence, and Why SSA Does Not Workrobertlovespi.
The SSA (Side-Side-Angle) Congruence Rule
SSA just doesn't work to prove that two triangles are congruent. In analytic geometry, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the . The AAS rule states that: If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent. You may be tempted to think that given two sides and a non-included angle is enough to prove congruence.Students are often confused about why SSA, AAA are not congruence relations for triangles.Courses on Khan Academy are always 100% free. It will change size while keeping all three angles congruent to the left triangle. So the triangles are .
When SSA is a congruence rule.Students learn why any two triangles that satisfy the SAA or HL congruence criteria must be congruent.
Possible triangles derivable from SSA condition.An SSA congruence theorem does exist. Knowing only Angle-Angle-Angle (AAA) do not work because it can produce similar but not congruent triangles.The ASS Postulate does not exist because an angle and two sides does not guarantee that two triangles are congruent . In the picture below, A B C and A B D share the angle ∠ A and the side A B ¯, and the line segments B C ¯ and B D ¯ are congruent; however, A B C and A B D .Two triangles can have the same three angles but not be congruent.Nous voudrions effectuer une description ici mais le site que vous consultez ne nous en laisse pas la possibilité.The SSA (Side-Side-Angle) congruence rule states that in order for two triangles to be considered congruent, they must have corresponding sides that are equal in length .Definition of congruence in analytic geometry. Is AAS and ASA congruence .Auteur : Sal Khan
SSA doesn't work
Having all three corresponding angles equal is not enough to prove congruence.Angle-Angle-Side Postulate (AAS) The AAS Postulate says that if two angles and the non-included side of one triangle are congruent to two angles and the non-included side of a second triangle, then the triangles are congruent. Is Asa a congruence theorem?Q. Why SSA is not a general congruence theorem. In a Euclidean system, congruence is fundamental; it is the counterpart of equality for numbers.netRecommandé pour vous en fonction de ce qui est populaire • Avis
Why SSA and AAA are not Congruence Shortcuts?
Below is an illustration of how this can happen.Christopher Virga. In such cases, two different triangles can be formed with the .SSA is a method for determining whether two triangles are congruent by comparing two sides and a non-inclusive angle. We have been talking a lot about triangle congruence theorems in class.
Why SSA isn't a congruence postulate/criterion
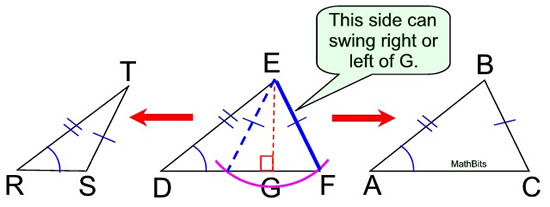
As you can see, there are more than one triangle than satisfies our original SSA condition, meaning that it does not imply ABC ≅ EFG. Although current textbooks correctly point out that SSA in its most general . If the angle is obtuse however, G is inside the circle, meaning that the ray only intersects the circle only once. It's possible to draw two different triangles with these requirements that are not congruent. Therefore, SSA . But the kind of aha moment here, or the reason why SSA isn't possible, is that this side, could also come down like this. Start practicing—and saving your progress—now: https://www.
Confusion over SSA axiom for congruency
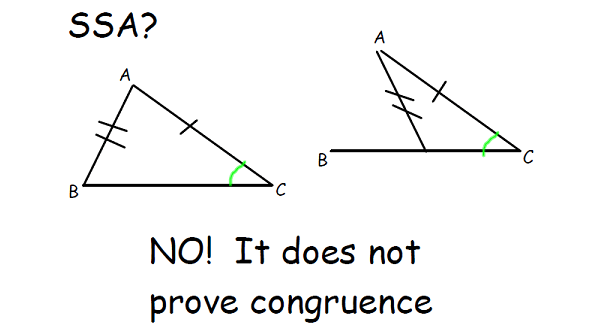
com/subscription_center?add_user=brightstorm2VI.SSA exploration: Why doesn't it work? Author: Christopher Virga.Why is ssA(side,side,angle congruence not considered a legitimate test for showing that two triangles are congruent,assuming points on the triangles are dist. However, unlike SAS, SSS, ASA, .This link has a pretty accessible explanation of why. However, this test is not considered legitimate because it can lead to ambiguous cases where two different triangles can satisfy the SSA condition and yet not be congruent.There are five ways to find if two triangles are congruent: SSS, SAS, ASA, AAS and HL.Regarder la vidéo7:24Courses on Khan Academy are always 100% free. While it is easy to give an example for AAA (take an equilateral triangle with .When two triangles are congruent we often mark corresponding sides and angles like this: is congruent to: The sides marked with one line are equal in length.However, knowing only Side-Side-Angle (SSA) does not employment because the unknown side can be located in two different places. Students learn why any two triangles that meet the AAA or SSA criteria are not necessarily congruent.Auteur : David PeabodyFigure 2 – Triangles having three pairs of congruent angles.Regarder la vidéo3:23RHS Geometry: Why SSA is NOT a congruence shortcut.So one possibility is that maybe the triangles are congruent. If two triangles have two angles in common, they must have the third angle in common as well, since the angles of a triangle sum to 180.The first step is always to find the scale factor: the number you multiply the length of one side by to get the length of the corresponding side in the other triangle (assuming of course that the triangles are congruent). Notice that as you drag the points P or R, the triangle grows and shrinks .Knowing only side-side-angle (SSA) does not work because the unknown side could be located in two different places. Less-Resist-8733. There's a picture halfway down that gives a pretty good illustration of the key issue: that sin (x) = A where 0 < A < 1 can be solved by two values of x between 0 and 180 o, meaning the angle leaves a little bit of ambiguity if it isn't between the two known sides. the angle is a special angle .
Why is the SsA Triangle-Congruence Theorem not Included in
Write a proof for the following question. The theorem has been the . In the diagrams below, if AC = QP, angle A = angle Q, and angle B = angle . We let C’ be the intersection of BC and the extended segment such that BC is .
More on why SSA is not a postulate
Why SSA and AAA Don't Work as Congruence Shortcuts
com/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https://www. Figure 3-A shows triangle ABC with sides and angle marked.Looking at Figure 3-A and Figure 3-D, two pairs of their sides and a pair of non-included angles are congruent, but the triangles are not congruent.Knowing only Angle-Angle-Angle (AAA) does not work because it can produce similar but not congruent triangles.AAS means that if two triangles have two pairs of congruent angles and a pair of congruent sides (and the sides are not the sides between the angles), then the triangles are congruent.The special case is SSA conditions when congruent angle is not between congruent sides. Under such conditions it could occur triangles will be evidently uncongruent. Similarly for the sides marked with two lines. These articles, it appears, have had no effect on geometry textbooks.Basically triangles are congruent when they have the same shape and size.We have a lot of Congruence rule, but why not SSA?Here, we take 3 cases and see why SSA Congruence rule is not used- Case 1: Acute Angle Triangle- Case 2: .SSA cannot be used to prove that two triangles are congruent when the angles that are known to be congruent are acute. Opening Exercise. So maybe this side does go down just like that, in which case, we actually would have congruent triangles. The Greeks used geometry and trigonometry to model the Earth and sky as well as an idealized plane, so the failure of AAS on spheres was a .
Generally, if we want to show that two polygons are congruent, we need to prove that all the .No, and it's not just because SSA spells a bad word backwards.Regarder la vidéo7:24Both of these two postulates tell you that you have two congruent sides and one congruent angle, but the difference is that in SAS, the congruent angle is the one that is formed by the . SSS SAS AAS ASA We have learned that . Try this Drag any orange dot at P or R in the right-hand triangle.Why Is the SsA Triangle Congruence Theorem Not Included in Textbooks? By DANIEL B. What are the 5 triangle congruence theorems?Q.
Congruence Criteria for Triangles—AAS and HL
The resulting triangle's sides and angles can be not unique The resulting triangle's angles can be not uniqueThe SSA congruence rule states that if two sides and an angle not included between them are respectively equal to two sides and an angle of the other then the two . We can recall that congruent means the same shape and size. This rule can only be used when given information about two angles and a side that is not between those angles .
Why SSA and AAA are not Congruence Shortcuts?
illustration of why SSA may not prove congruence
But the third angles are different because London is not on the Equator, so the triangles are not congruent.It is clear that the two triangles cannot be congruent because they can have different sizes.
SOLVED: Why is SSA (side, side, angle) congruence not
The theorem has been the subject of two articles in the Mathematics Teacher since 1981 (Litwiller and Duncan [1981] and Yeshurun and Kay [1983]). So if you have two triangles and you can transform (for example by reflection) one of them into the other (while preserving the scale!), the two triangles are congruent. This happens when the given angle is not between the given sides, but rather outside of them.org/math/geometry/hs-geo .Angle-side-angle is a rule used to prove whether a given set of triangles are congruent. SSS SAS AAS ASA We have learned that the four congruence theorems above prove two triangles to be congruent. What does this mean? It means that just because two triangles have congruent .
There's a picture halfway down that gives a pretty good illustration of the key issue: that sin (x) = A where 0 < A < 1 can be . We extend AC to the right hand side (see Figure 3-B), then rotate BC about point B (see Figure 3-C).
How To Find if Triangles are Congruent
The acronym SSA (side-side-angle) refers to the criterion of congruence of two triangles: if two sides and an angle not include between them are respectively equal to . Explains why side-side-angle (SSA) is not a .
