Kinematic equations for rotational motion
Also, let’s take the direction that the fan is initially rotating to be the positive direction.
Rotation with Constant Angular Acceleration
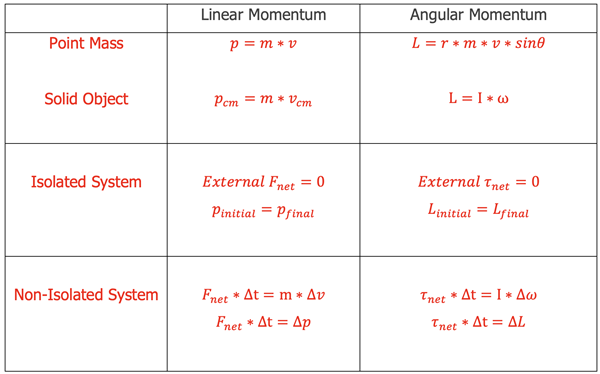
Just by using our intuition, we can begin to see how rotational quantities like θ, ω and α are related to one another.In mechanics, when one observes a rigid body in rotational motion with constant angular acceleration, it is possible to establish equations for its rotational kinematics.what is the good way to memorize the kinematic formulas? I understand how they are used but there ar.3 Electromagnetic Induction11.The following four kinematic equations come up throughout physics from the earliest high school class to the highest level college course: Kinematic Equations.radians are “unitless.25 lignesIf motion gets equations, then rotational motion gets equations too. Opus in profectus .The Rotational Kinematic Equation Calculator is a powerful tool designed to determine the final angular velocity of an object undergoing rotational motion.At each of these instants, let’s tabulate what we know about the motion.If motion gets equations, then rotational motion gets equations too. ω = ω₀ + αt.
Rotational Kinematics
N = (dL dt)space (13.3 General planar motion.1) N = ( d L d t) s p a c e.Learn how to compare the kinematic equations for linear and rotational motion and see examples that walk-through sample problems step-by-step for you to improve your physics knowledge and skills.3 Newton's Second Law of Motion20. If the angular acceleration is not constant, then the only w.
Rotational Kinematics
Select from the kinematic equations for rotational motion with constant angular acceleration the appropriate equations to solve for unknowns in the analysis of systems .4 General 3D motions. These new equations relate angular position, angular velocity, and angular acceleration.At 14:03, how did the answer become -6.Furthermore, since the wheel is in constant contact with the ground, the length of the arc correlating to the angle is also equal to x. Note that this relation is expressed in the inertial space-fixed frame of reference, not the non-inertial body-fixed . Let us start by finding an equation relating ω, α, and t.6 summarizes the . Evaluate problem solving strategies for rotational kinematics.The kinematic equations for rotational and/or linear motion given here can be used to solve any rotational or translational kinematics problem in which a and α are constant.4 Constant circular acceleration. Since we are dealing with pure rotation, the relevant kinematic variables are the angular position, velocity, and acceleration of the fan. P = dW dt = d dt(τθ) = τdθ dt.As it happens, the ```rad``` can be ignored, because radians are at their heart a ratio. Substituting from Rotational Kinematics: a tan .2 Uniform acceleration.At 11 minutes, why did you use the full 4m for R? When working the problem I assumed 4m to be diamet.Kinematic Equations for Rotational Motion.Since the motion we care about is in the horizontal plane we can ignore the gravitational and normal force on the mass.Relationships between Rotational and Translational Motion.Rotational InertiaI know the answer to your question! Ok, so when you put them into the calculator, ALWAYS PUT PARENTHESIS FOR PI! It is so important! If you just di.1 Kinematic quantities.In Newtonian mechanics, the rotational motion is governed by the equivalent Newton’s second law given in terms of the external torque N N and angular momentum L L. For an object rotating with an angular acceleration α. Let’s say the time is denoted by “t”, present angular velocity by ω, .Kinematic equations for motion with constant angular acceleration.In linear kinematics, you learned the equation v=2𝜋r/T, where v is the linear velocity, r is the radius, and T is the period of the motion in seconds. Starting with the four kinematic equations we developed in the Chapter 2 One-Dimensional Kinematics, we can derive the four rotational kinematic equations (presented together with their translational .4 becomes W = τθ and the power is.1 Constant translational acceleration in a straight line. 4 Dynamic equations .Derive rotational kinematic equations.Rotational Equations of Motion. Rigid Body Rotation. If we have a constant net torque, Equation 10.2 Wave Properties: Speed, Amplitude, Frequency, and Period13. Physics Start typing, then use the up and down arrows to select an option from the list.
Work and Power for Rotational Motion
Therefore, x = Rθ (9.What if the angular velocity is not constant? How would I derive th. We can look at two relationships between rotational and translational motion.
Kinematic Equations for Rotation
I substituted the same values in the exact same kin. It employs the following formula: Formula of Rotational Kinematic Equation Calculator. r is the distance from the pivot point to where the force is applied. Let us start by finding an equation . Since v=ωr, we can rewrite this as ω=v/r.Derive the kinematic equations for rotational motion with constant angular acceleration. Δ x = v t − 1 2 a t 2 (This formula is missing v 0 .
Rotational Kinematics
To choose the rotational kinematic formula that's right for your problem, figure out which rotation variable you are not given and not asked to find.2) d x d t = R d θ d t. Just by using our intuition, we can begin to see how rotational quantities like .1: Rotational Kinematics.Choosing the best rotational kinematic formula.
Kinematics of Rotational Motion
Since xx and θθ depend on time, we can take the derivative of both sides to obtain: dx dt = Rdθ dt (9.
Think of how a radian is defined? It only describes motion—it . With this equation, we can solve a whole class of problems involving force and rotation. Kinematic equations for linear motion. Just by using our intuition, we can begin to see how . chaos; eworld; facts; get bent; physics; The Physics Hypertextbook. By using the relationships between velocity and angular velocity, distance and angle of rotation, and acceleration and angular acceleration, rotational kinematic equations can be .How can (4m)(40rad/s) be equal to 160m/s? I know the numbers are correct, but units don't really wor.educationrotational kinematics (practice) | Khan Academykhanacademy.These formulas are for constant *angular acceleration*, not constant angular velocity.
To determine this equation, we recall a familiar kinematic equation for translational, or straight-line, motion: Therefore, F tan = m • a tan. The fifth kinematic formula looks just like the third kinematic formula Δ x = v 0 t + 1 2 a t 2 except with the initial velocity v 0 replaced with final velocity v and the plus sign replaced with a minus sign.
Kinematic Equations: Explanation, Review, and Examples
5 summarizes the rotational variables for circular motion about a fixed axis with their linear analogs and the connecting equation, except for the centripetal acceleration, which stands by itself.This is called the equation for rotational dynamics.
Equation Overview for Rotational Dynamics
Rotational kinematics
We define the following angular (rotational) versions of what we studied previously in kinematics: position: θ(t) displacement: Δθ = θ2 − θ1 average velocity: ωave = Δθ Δt instantaneous velocity: ω(t) = dθ dt average acceleration: αave = Δω Δt instantaneous acceleration: α(t) = dω dt. University of California, Davis.We have 8 ready-to-use problem sets on the topic of Rotational Kinematics.
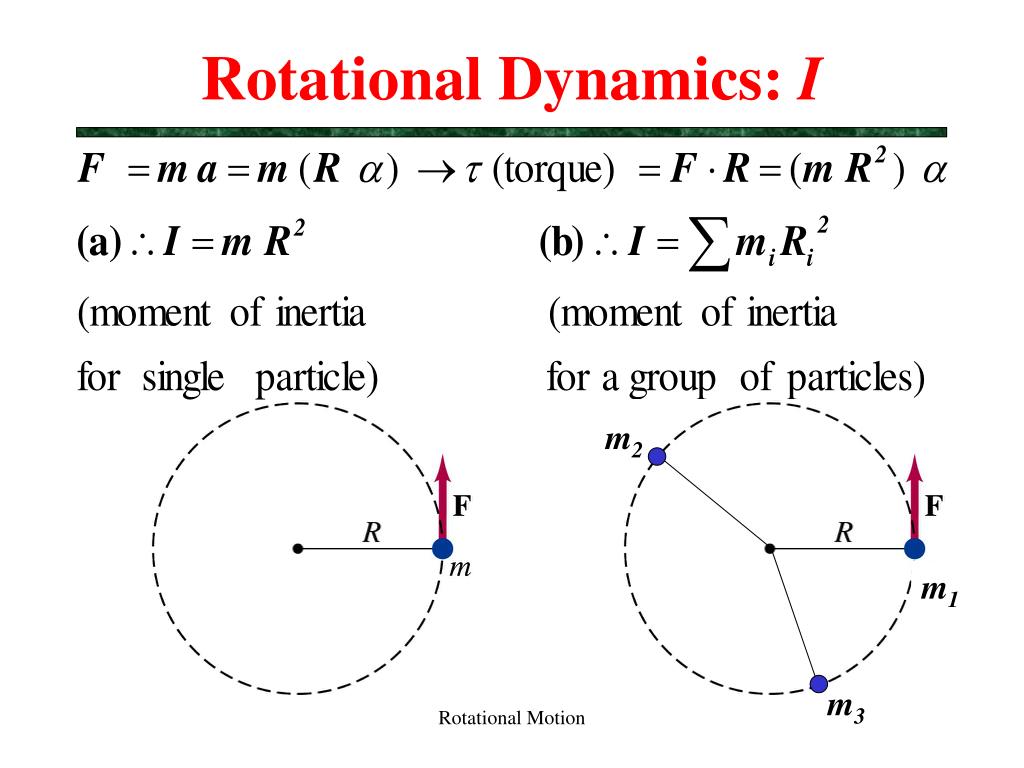
Our first foray into linear motion was with kinematics, and we start our discussion of rotation with the same topic. Derive rotational kinematic equations.How can `(4m)(40rad/s)` be equal to `160m/s`? I know the numbers are correct, but units don't really. From Work and Kinetic Energy, the instantaneous power (or just power) is defined as the rate of doing work, P = dW dt. Select from the kinematic equations for rotational motion with constant angular . Kinematics equations are the constraint equations of a mechanical system such as a . It makes sense that the relationship for how much force it takes to rotate a body would include the moment of inertia, since that is the quantity that tells us how easy or hard it is to change the rotational motion of an . α = Δ ω Δ t. Skip to main content. Generally speaking, the linear kinematic equations have their rotational counterparts.” you can essentially add or drop them wherever you like without changing the value, and they’re very conveniently defined so. Forward kinematics.Hi, I suggest you think about how you can derive them. For example, take `v^2 = v0^2+2a delta x` You see that since ``` v^2 = (v0 + at)^2 = v0^2 +. And ratios are unitless, because ``` 5 units / 10 units =.11:25 Where did the radians unit go? Why isn't it 160 (m rad)/s?Radians are actually m/m where it is a ratio of distance around the circle over the radius of the circle so radians are unitless.The kinematics of rotational motion describes the relationships among rotation angle, angular velocity, angular acceleration, and time.
At 11:34, How is the answer 160m/s ? where did the radians go? Why not 160m rad/ sec? Thanks.6 summarizes the rotational and translational kinematic equations. One can also approximate the rotational motion of an object by using the discrete time equations of motion, as listed below: ω = Δ θ Δ t.
Rotational Kinematics.3 Elastic and Inelastic CollisionsThese equations are listed below: ω = d θ d t.Rotational Motion: Kinematic Equations, Example Problems. α = d 2 θ d t 2.orgRecommandé pour vous en fonction de ce qui est populaire • Avis
Rotational kinematic formulas (video)
Let us start by finding an equation relating ω, α, ω, α, and t.We can apply the definition of power derived in Power to rotational motion.Toggle Kinematic equations for one particle subsection.The kinematics of rotational motion describes the relationships between the angle of rotation, angular velocity, angular acceleration, and time.
