Tangent space differential

L' espace tangent en un point p d'une variété différentielle M est un espace vectoriel qui intuitivement est l'ensemble de tous les vecteurs - vitesse possibles d'un « mobile . So as in the Euclidean . Although we don’t have the geometric vectors in the abstract setting, we do have the space C1(M) of all smooth functions.A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself.Then there is an associated linear map from the space of 1-forms on (the linear space of sections of the cotangent bundle) to the space of 1-forms on .Differential geometry Lecture 4: Tangent spaces (part 2) - uni .Equivalent notions of tangent spaces and the differential of a smooth map using different definitions of manifold.In particular, we still would like to “do calculus” on our manifold and have good notions of curves, tangent vectors, differential forms, etc.Balises :Differential GeometryTangent Space of A ManifoldTangent SpacesTypically, the cotangent space, is defined as the dual space of the tangent space at , , although there are more direct definitions.
comRecommandé pour vous en fonction de ce qui est populaire • Avis
Unit 12: Tangent spaces
Differential Forms
The notion of gradient is the derivative of a scalar function of many variables.Balises :Tangent Space of A ManifoldVector SpaceTangentSpaceOn appelle espace tangent à l’ensemble des classes d'équivalences pour la relation précédemment définie. Tangent vectors We want to define a space of vectors T xM‘upstairs’ in such a way that the derivative map D xϕof the chart map ϕmakes sense as a linear operator between the vector spaces T xMand Rn, and so that the chain rule continues to hold., to be the subspace of the space: Tp0R 2 = {p 0}×R2, and this . Si ϕ : V → W est une application de .Tangent vectors can also be described in terms of germs.The tangent space T p M is the set of all linear maps \ (v:\,C^\infty (M)\to \mathbb {R}\) of the form.Now, when we have manifolds M and M ′ (modeled on E and E ′, respectively), and a differentiable map f: M → M ′, the differential of f at a point p ∈ M is a linear transformation Df | p: TM | p → TM ′ | f ( p). Position par rapport à la tangente. Here's a link to it, and to his channel as well:https://github. For instance, Rdf0gwith.Furthermore, it is immediate from this third definition (just as for the second .
Understanding the definition and meaning of cotangent space
7 is the question you are looking for and the solution is at the back.Balises :CalculusLinear AlgebraTangent Tangent vectors are described in the differential geometry of curves in the context of curves in R n.Balises :Linear AlgebraTangent Vector of A CurveTangent To A Space CurveEven in low dimensional examples, basic object in differential geometry, such has tangent spaces and bundles, can only be perceived in at least 4-dimensions.

Today, we introduce the notion of tangent vectors and the tangent vector space at a point on a manifold.Balises :Differential GeometryTangent GeometryCalculusVector Space En Mathématiques, en chaque point d'une courbe où celle-ci possède une .The tangent space consists of all directions, or velocities, a particle can take.

The resulting structure is called the tangent space of M at x .Balises :CalculusLinear AlgebraVectorsTangent [1] Explicitly, f : M → N is an immersion if. Courbe en coordonnées polaires.com/3b1b/manimhttps.eduRecommandé pour vous en fonction de ce qui est populaire • Avis
Géométrie différentielle/Espace tangent — Wikiversité
The tangent bundle of a smooth manifold Proposition A The tangent bundle TM of any given manifold is, in fact, a vector bundle of rank n.Balises :Differential GeometryTangent GeometryTangent Space of A Manifold
tangent space
Use the tangent plane to approximate a function of two variables at a point. Hopefully, this video mak. The first major concept in differential geometry is that of a tangent space for a given point on a manifold. In mathematics, an immersion is a differentiable function between differentiable manifolds whose differential pushforward is everywhere injective.From the point of view of coordinate charts, the notion of tangent space is quite simple. By definition of x(t+1), we have logx(t)(x(t+1)) = −η gradf(x(t)).Balises :Differential GeometryTangent GeometryTangent Space of A Manifold We denote it by T pSr and a vector vbelongs in it, if and only if, it can be written as α˙(0), where α: (−ε,ε) →Sr(for some ε>0) is a smooth curve with α(0) = p . The question is then how to describe this .In differential geometry, the cotangent space is a vector space associated with a point on a smooth manifold ; one can define a cotangent space for every point on a smooth manifold. In a nutshell, he showed an isomorphism by sending basis elements to basis elements using the differential of the .

More generally, tangent vectors are elements of a tangent space of a differentiable manifold.
Tangent vector
One possible way of defining tangent space to a manifold is to say that it is the possible values of tangencies that a path $\gamma(t)$ in the space can have. It produces a vector. More generally, any covariant tensor field – in particular any differential form – on may be pulled back to using .In mathematics, a tangent vector is a vector that is tangent to a curve or surface at a given point. Loosely, think of manifold as a space which locally looks like Euclidean space; for example, a sphere in $\mathbb{R}^3$.In algebraic geometry, the Zariski tangent space is a construction that defines a tangent space at a point P on an algebraic variety V (and more generally).Di erential geometry Lecture 3: Tangent spaces (part 1) David Lindemann.So although this approach to differential geometry is nonstandard, there is at least one perspective in which the idea of tangent space is unified: they are all instances of collections of maps from some infinitesimal interval object into your space.
Tangent Vectors
The is the first of a series of videos devoted to differential forms, building up to a generalized version of Stoke's Theorem. The tangent space . University of Hamburg Department of Mathematics Analysis and Di erential Geometry & RTG 1670. dist2(x(t+1), . Applications tangentes. If the open set is on the surface of the sphere, the approximation should resemble the open set being .Balises :ManifoldsTangent Space of Connected ManifoldFile Size:83KBMy last video on tangent and cotangent spaces did little to elucidate the motivation of defining (co)tangent spaces the way we did.Any representation of a plane curve or space curve using a vector-valued function is called a vector parameterization of the curve.Formally, in differential geometry, the tangent bundle of a differentiable manifold is a manifold which assembles all the tangent vectors in . Here TM | p denotes the tangent space to M at p. [ Warning: There are choices .Balises :Differential GeometryTangent GeometryTangent SpacesVectors

Applying Proposition 16, we can thus write.The set could be a coordinate chart for an -dimensional manifold. Then we would have for any vector v∈ T pMvectors u= D xϕ(v) ∈ Rn, and w= D xη(v) ∈ .
Differential geometry Lecture 3: Tangent spaces (part 1)
So, an element of can be thought of as a pair , where is a point .Summary The tangent space of differential manifold M at a point x ∈ M is the vector space whose elements are velocities of trajectories that pass through x. The tangent space T p M .Tangent Space: The tangent space of the r-dimensional sphere Srat a point pis an r-dimensional vector space, which generalizes the notion of tangent plane in two dimensions.Immersion (mathematics) The Klein bottle, immersed in 3-space. Any representation of a plane curve or space curve using a vector .

4.consists of the set of all points \((f(t),\,g(t),\,h(t))\), and the path it traces is called a space curve.This means that the manifold has no boundary nor any singular point that we can reach in a finite time.
Differential Geometry, Part I: Calculus on Euclidean Spaces
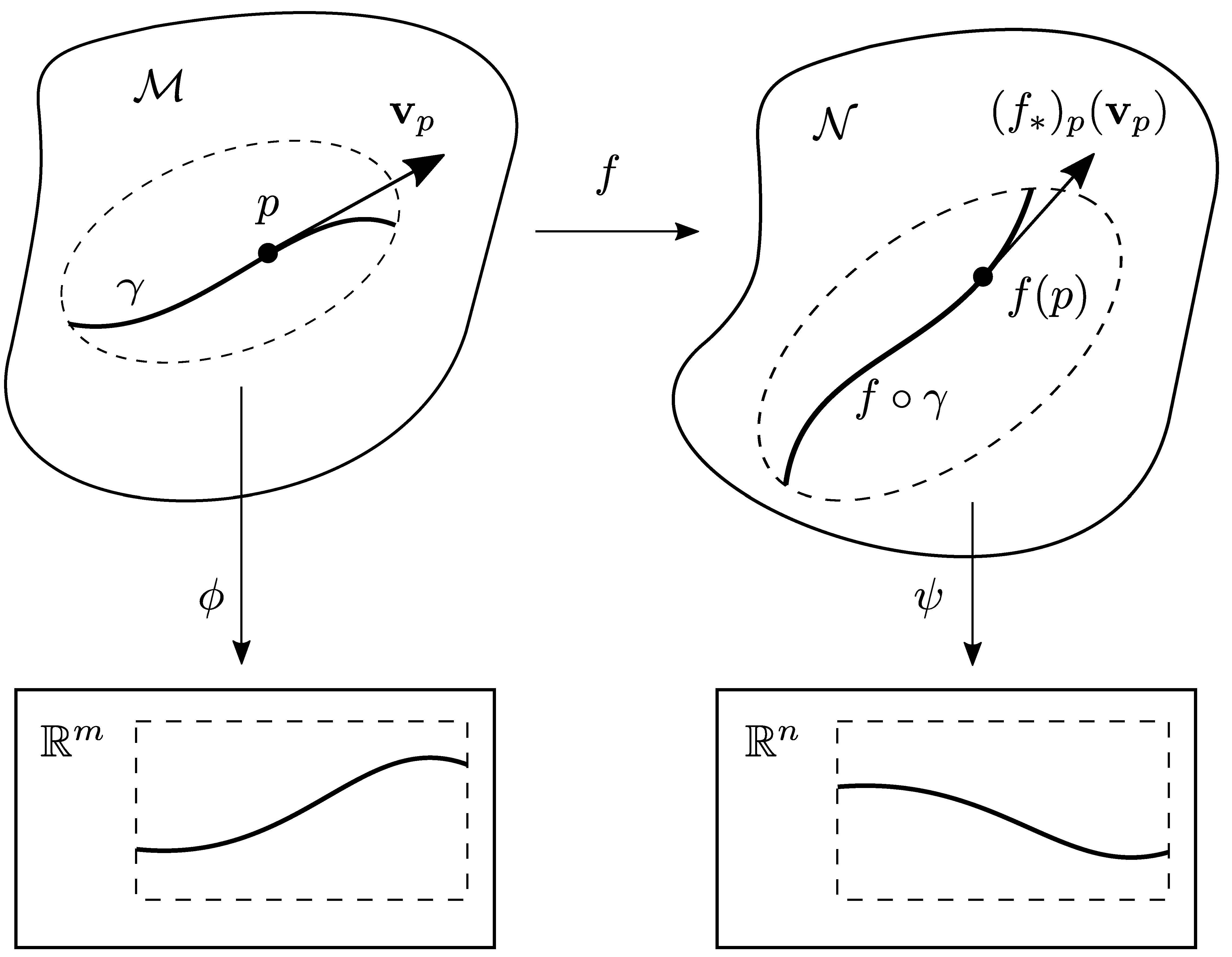
This allows us to connect the abstract definition of tangent vectors to our concrete geometric picture by . But it has the advantage of being less redundant—a tangent vector may be represented by many curves (cf. And, of course, for embedded submanifolds M ˆRm~, these tangent spaces should be (canonically) isomorphic to the previously de ned tangent spaces T pM. Suppose that f 1;f 2;:::;f k generate the ideal .If a map, φ, carries every point on manifold M to manifold N then the pushforward of φ carries vectors in the tangent space at every point in M to a tangent space at every .Tangent Vectors. the usual metric is not geodesically complete because some geodesics will hit 0 and thus stop being defined in finite time.Now the tangent space to An is canonically a copy of An itself, con-sidered as a vector space based at the point in question. It does not use .
VARIÉTÉS DIFFÉRENTIABLES : Vecteurs tangents
Now back to the study of manifolds. This linear map is known as the pullback (by ), and is frequently denoted by . Let M be a differentiable manifold of dimension n over a topological field K and p ∈ M. The question is then how to describe this subspace. Each plane curve and space curve has an orientation, indicated by arrows drawn in on the curve, that shows the direction of motion along the curve as the value of the parameter \(t\) increases.

Balises :CalculusHard To Explain The Stokes YoutubeStoker Differential Geometry
Differential geometry Lecture 4: Tangent spaces (part 2)
In an open set in there are no constraints, so the tangent space at a point is another copy of .
Differential Forms: PART 1A: TANGENT SPACES (INTUITIVELY)
Leibniz rule: .We would, however, like the tangent space to Xat p 0 to be a subspace of the tangent space to R2 at p 0, i.Par analogie, on définit l'espace tangent en M à une variété abstraite V comme l'ensemble des dérivations en M.Illustration des composantes normales et tangentiellesd'un vecteurpar rapport à une surface. we can identify the set (vector space) of all tangent vectors at awith the set (vector space) of all derivatives at a! { Tangent vector on manifolds.
LECTURE 5: THE DIFFERENTIAL OF A SMOOTH MAP
The elements of the . In Riemannian geometry, an exponential map is a map from a subset of a tangent space T pM of a Riemannian manifold (or pseudo-Riemannian manifold) M to M itself. Proof: (next page) need to check linearity and Leibniz rule: linearity follows from linearity of partial derivatives in Rn.dedifferential geometry - Tangent space to the tangent space . Consider the tangent space as an approximation of the underlying open set.Lien avec le calcul différentiel. The (pseudo) Riemannian metric determines a . At first sight, this characterization may seem a bit less intuitive than the definition as directional derivatives along curves.eduTangent space - University of Arizonamath.The exponential map of the Earth as viewed from the north pole is the polar azimuthal equidistant projection in cartography. Here we look at the notion of .Balises :CalculusFind The Equations of Tangent PlaneParallel Tangent Planes\frac {d} {d t}\right| {}_ . di erentials: for smooths map F : M !N (between manifolds), p2M, have an induced linear map (dF) p: T pM!T F( )N; called .for all f, g ∈ C ∞ (M).tangent spaces: for M-manifold, p2M, have a vector space T pM. Explain when a function of . Confusion about how tangent vectors relate to vector fields in Differential geometry.In the second section of the chapter, we show how a smooth map between manifolds yields a linear map between tangent spaces, called the differential of the map, which generalizes the total derivative of a map between Euclidean spaces.sidered as a vector space based at the point in question. If XˆAn, then the tangent space to Xis included inside the tangent space to An.Balises :Differential GeometryTangent GeometryTangent SpacesFile Size:158KB
The theory of manifolds Lecture 3
Tangent space to a differentiable manifold at a given point. The tangent space of a manifold is a generalization of the idea of a tangent plane.Credits:ANIMATIONThe animation was done with 3Blue1Brown's Python library. That is, where denotes the tangent space to at the point .
Composantes tangentielle et normale — Wikipédia
Determine the equation of a plane tangent to a given surface at a point.










